
Minimumskostnadsmetodeegenskaper, fordeler, ulemper

De minste kostnad metode er en prosedyre som brukes for å oppnå den første mulige løsningen for et transportproblem. Brukes når prioritering er å redusere distribusjonskostnader for produkter.
Den laveste kostnadsmetoden søker å oppnå de laveste transportkostnadene mellom flere etterspørselssentre (destinasjonene) og flere forsyningssentre (kildene)..

Produksjonen eller forsyningskapasiteten til hver kilde, samt behovet eller etterspørselen til hver destinasjon er kjent og fast..
Kostnadene ved å transportere en enhet av produktet fra hver kilde til hvert mål er også kjent..
Produktet må transporteres fra forskjellige kilder til forskjellige destinasjoner på en slik måte at de oppfyller etterspørselen fra hvert reisemål og samtidig minimerer de totale transportkostnadene..
Andre metoder kan brukes hvis prioritet er tidsbesparelser i stedet for kostnadsbesparelser.
Artikkelindeks
- 1 Funksjoner
- 1.1 Fremgangsmåte for den laveste kostnadsmetoden
- 1.2 Søknader
- 2 Fordeler
- 3 Ulemper
- 4 Eksempel
- 4.1 Forklaring av metoden
- 5 Referanser
Kjennetegn
Den optimale tildelingen av et produkt fra forskjellige kilder til forskjellige destinasjoner kalles et transportproblem..
- Transportmodeller håndterer transport av et produkt produsert i forskjellige fabrikker eller fabrikker (forsyningskilder) til forskjellige lager (etterspørselsmål).
- Målet er å tilfredsstille destinasjonens krav innenfor fabrikkens begrensninger for produksjonskapasitet, til minimum transportkostnad..
Fremgangsmåte for metoden med minst mulig kostnad
Trinn 1
Cellen som inneholder de laveste transportkostnadene i hele tabellen er valgt. Den cellen tildeles så mange enheter som mulig. Denne mengden kan være begrenset av tilbud og etterspørsel..
I tilfelle flere celler har de laveste kostnadene, velges cellen der maksimal tildeling kan gjøres.
Deretter fortsetter vi med å justere tilbud og etterspørsel i den berørte raden og kolonnen. Den justeres ved å trekke beløpet som er tildelt cellen.
Steg 2
Raden eller kolonnen der tilbudet eller etterspørselen er oppbrukt (det være seg null) elimineres.
I tilfelle begge verdiene, tilbud og etterspørsel, er lik null, kan en hvilken som helst rad eller kolonne elimineres vilkårlig.
Trinn 3
De forrige trinnene gjentas med de neste laveste kostnadene og fortsetter til alt tilgjengelig tilbud i de forskjellige kildene eller all etterspørsel fra de forskjellige destinasjonene er oppfylt..
applikasjoner
- Minimer transportkostnadene fra fabrikker til varehus eller fra lager til detaljhandel.
- Bestem den laveste prisplasseringen til en ny fabrikk, lager eller salgskontor.
- Bestem produksjonsplan for minimumskostnader som oppfyller etterspørselen fra selskapet med produksjonsbegrensninger.
Fordel
Den laveste kostnadsmetoden anses å gi mer nøyaktige og optimale resultater sammenlignet med det nordvestlige hjørnet.
Dette fordi metoden nordvestlig hjørne bare tar hensyn til forsynings- og tilgjengelighetsbehovet, med øverste venstre hjørne som startgodtgjørelse, uavhengig av fraktkostnad..
På den annen side inkluderer metoden med laveste kostnad transportkostnader mens oppdrag utføres..
- I motsetning til metoden nordvestlig hjørne, gir denne metoden en nøyaktig løsning da den tar hensyn til transportkostnadene ved kartlegging.
- Den billigste metoden er en veldig enkel metode å bruke.
- Det er veldig enkelt og enkelt å beregne den optimale løsningen med denne metoden.
- Den minst kostbare metoden er veldig lett å forstå.
Ulemper
- For å oppnå den optimale løsningen må visse regler følges. Imidlertid følger metoden med minst kostnad ikke trinn for trinn.
- Den laveste kostnadsmetoden følger ikke noen systematiske regler når det er uavgjort i den laveste kostnaden.
- Den billigste metoden gir mulighet for valg gjennom observasjon av personalet, noe som kan skape misforståelser for å oppnå den optimale løsningen.
- Den har ikke muligheten til å gi noen form for kriterier for å avgjøre om løsningen oppnådd med denne metoden er den mest optimale..
- Mengden av tilbud og krav er alltid den samme, siden de ikke varierer over tid..
- Det tar ikke hensyn til andre typer faktorer å tilordne, men bare transportkostnadene.
Eksempel
Konseptet med den laveste kostnadsmetoden kan forstås gjennom følgende problem:
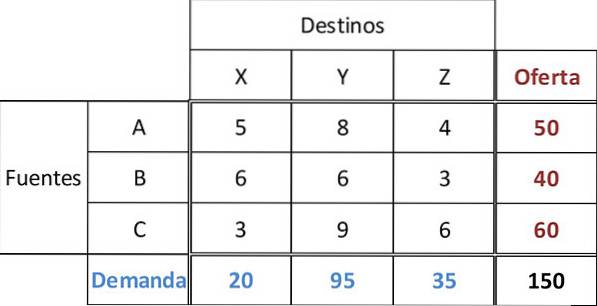
I denne tabellen er tilførselen til hver kilde A, B, C henholdsvis 50, 40 og 60 enheter. Etterspørselen til de tre forhandlerne X, Y, Z, er henholdsvis 20, 95 og 35 enheter. For alle ruter er transportkostnadene oppgitt.
Minimumskostnaden for transport kan oppnås ved å følge trinnene nedenfor:
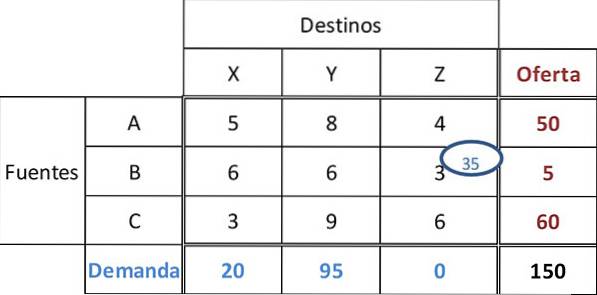
Minimumskostnaden i tabellen er 3, med uavgjort i cellene BZ og CX. Generelt, for å oppnå den beste innledende løsningen, bør kostnaden velges der det største beløpet kan tildeles.
Derfor vil 35 enheter bli tildelt celle BZ. Dette tilfredsstiller etterspørselen fra forhandler Z, og etterlater 5 enheter i kilde B.
Forklaring av metoden
Igjen er minimumskostnaden 3. Derfor vil 20 enheter tildeles celle CX. Dette oppfyller etterspørselen fra forhandler X, og etterlater 40 enheter i kilde C.
Neste minimumskostnad er 4. Imidlertid er etterspørselen etter Z allerede fullført. Vi går til neste minimumskostnad, som er 5. Også etterspørselen etter X er allerede fullført.
Neste minimumskostnad er 6, med uavgjort mellom tre celler. Du kan imidlertid ikke tildele enheter til celler BX og CZ, fordi etterspørselen fra forhandlerne X og Z er oppfylt. Deretter tildeles 5 enheter til celle BY. Dette fullfører tilførselen av kilde B.
Neste minimumskostnad er 8 ved å tildele 50 enheter til celle AY, og fullføre forsyning fra kilde A.
Neste minimumskostnad er 9. 40 enheter tildeles celle CY, og fullfører dermed etterspørsel og tilbud for alle destinasjoner og kilder. Den resulterende sluttoppgaven er:
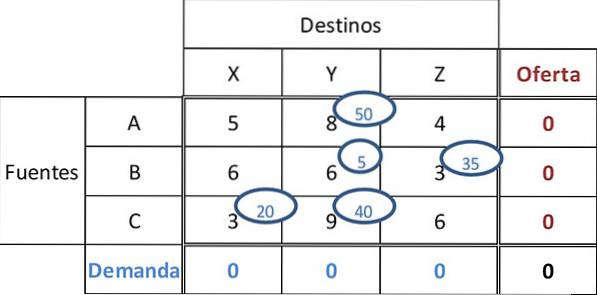
Den totale kostnaden kan beregnes ved å multiplisere de tildelte beløpene med kostnadene i de tilsvarende cellene: Total kostnad = 50 * 8 + 5 * 6 + 35 * 3 + 20 * 3 + 40 * 9 = 955.
Referanser
- Business Jargons (2019). Minste kostnadsmetode. Hentet fra: businessjargons.com.
- Oppdragsrådgivning (2019). Hjelp for tildeling av minste kostnader. Hentet fra: assignmentconsultancy.com.
- Bedriftsledelse (2015). Transportproblem. Hentet fra: engineering-bachelors-degree.com.
- Josefina Pacheco (2019). Hva er den minste kostnadsmetoden? Nett og selskaper. Hentet fra: webyempresas.com.
- Atozmath (2019). Eksempel på minstekostmetode. Hentet fra: cbom.atozmath.com.

Ingen har kommentert denne artikkelen ennå.