Gravity acceleration hva det er, hvordan det måles og øvelser

De akselerasjon av tyngdekraften eller gravitasjonsakselerasjon er definert som intensiteten til jordens gravitasjonsfelt. Det vil si kraften den utøver på ethvert objekt, per masseenhet.

Den er betegnet med den nå kjente bokstaven g, og dens omtrentlige verdi i nærheten av jordoverflaten er 9,8 m / s^to. Denne verdien kan oppleve små variasjoner med geografisk breddegrad og også med høyde i forhold til havnivå..

Gravitasjonsakselerasjonen, i tillegg til å ha den nevnte størrelsen, har retning og sans. Faktisk er det rettet vertikalt mot midten av jorden.

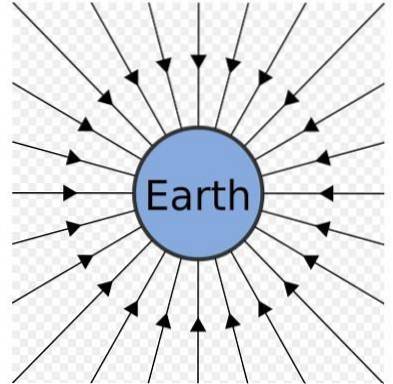
Jordens gravitasjonsfelt kan representeres som et sett med radiale linjer som peker mot sentrum, som vist i forrige figur.

Artikkelindeks

• 1 Hva er tyngdekraftens akselerasjon?
  • 1.1 Loven om universell gravitasjon
• 2 Hvordan måles tyngdekraften på forskjellige planeter?
  • 2.1 Eksperiment for å bestemme verdien av g
  • 2.2 Standardverdi av g på jorden, på månen og på Mars
  • 2.3 Tyngdekraften på månen
  • 2.4 Tyngdekraften på Mars
• 3 Øvelse løst: det fallende eplet
• 4 Referanser

Hva er tyngdekraftens akselerasjon?

Verdien av akselerasjonen av tyngdekraften på jorden eller på en hvilken som helst annen planet tilsvarer intensiteten til gravitasjonsfeltet den produserer, som ikke avhenger av gjenstandene rundt den, men bare av dens egen masse og radius..

Gravitasjonsakselerasjonen defineres ofte som akselerasjonen som oppleves av ethvert objekt i fritt fall i nærheten av jordoverflaten..

I praksis er dette det som nesten alltid skjer, som vi vil se i de følgende avsnittene, der Newtons lov om universell gravitasjon vil bli brukt..

Newton sies å ha oppdaget denne berømte loven mens han mediterte på fallende kropper under et tre. Da han kjente slaget av eplet på hodet, visste han straks at kraften som får eplet til å falle er den samme som får månen til å kretse rundt jorden.

Loven om universell gravitasjon

Enten legenden om eplet var sant eller ikke, skjønte Newton at størrelsen på tiltrekningskraften mellom to objekter, for eksempel mellom jorden og månen, eller jorden og eplet, må avhenge av massene deres:

Kjennetegn ved gravitasjonskraften

Gravitasjonskraften er alltid attraktiv; det vil si at de to kroppene det påvirker tiltrekker seg hverandre. Det motsatte er ikke mulig, siden banene til himmellegemene er lukkede eller åpne (for eksempel kometer) og en frastøtende kraft aldri kan produsere en lukket bane. Så massene tiltrekker seg alltid, uansett hva.

En ganske god tilnærming til jordens sanne form (m₁) Og av månen eller eplet (m_to) er å anta at de har en sfærisk form. Følgende figur er en representasjon av dette fenomenet.

Her både styrken utøvd av m₁ Omtrent m_to, som den som m_to Omtrent m₁, begge like store og rettet langs linjen som slutter seg til sentrene. De blir ikke kansellert, siden de brukes på forskjellige objekter.

I alle de følgende avsnittene antas det at gjenstandene er homogene og sfæriske, derfor faller tyngdepunktet sammen med deres geometriske sentrum. Det kan antas at all massen er konsentrert akkurat der.

Hvordan måler du tyngdekraften på forskjellige planeter?

Tyngdekraften kan måles med et gravimeter, et tyngdekraftsmålingsapparat som brukes i geofysiske gravimetriske undersøkelser. Foreløpig er de mye mer sofistikerte enn originalene, men i begynnelsen var de basert på pendelen.

Pendelen består av et tynt, lett og ikke-utvidbart tau med lengde L. Den ene enden er festet til en støtte og en masse m henges fra den andre..

Når systemet er i likevekt, henger massen vertikalt, men når den skilles fra den, begynner den å svinge og utfører en frem og tilbake bevegelse. Tyngdekraften er ansvarlig for det. For alt som følger er det gyldig å anta at tyngdekraften er den eneste kraften som virker på pendelen.

Perioden T for svingning av pendelen for små svingninger er gitt av følgende ligning:

Eksperiment for å bestemme verdien av g

Materialer

- 1 metallkule.

- Tau av flere forskjellige lengder, minst 5.

- Målebånd.

- Transportør.

- Kronometer.

- En brakett for å fikse pendelen.

- Grafpapir eller dataprogram med regneark.

Prosess

1. Velg en av strengene og monter pendelen. Mål lengden på strengen + sfærens radius. Dette vil være lengden L..
2. Fjern pendelen fra likevektsposisjonen med omtrent 5 grader (måle den med vinkelmåler) og la den svinge.
3. Start samtidig stoppeklokken og mål tiden på 10 svingninger. Skriv ned resultatet.
4. Gjenta fremgangsmåten ovenfor for de andre lengdene.
5. Finn tiden T det tar for pendelen å svinge (del hvert av resultatene ovenfor med 10).
6. Firkant hver oppnådd verdi, og oppnå T^to
7. På grafpapir grafer du hver verdi av T^to på den vertikale aksen, mot den respektive verdien av L på den horisontale aksen. Vær konsekvent med enhetene og ikke glem å ta hensyn til feilen i forståelsen av instrumentene som brukes: målebånd og stoppeklokke..
8. Tegn den beste linjen som passer til de plottede punktene.
9. Finn skråningen m av linjen ved hjelp av to punkter som hører til den (ikke nødvendigvis eksperimentelle punkter). Legg til den eksperimentelle feilen.
10. Ovennevnte trinn kan utføres med et regneark og muligheten til å konstruere og passe en rett linje.
11. Fra verdien av skråningen til fjern verdien av g med sin respektive eksperimentelle usikkerhet.

Standardverdi på g på jorden, på månen og på Mars

Standardverdien for tyngdekraften på jorden er: 9,81 m / s^to, på 45º nordlig bredde og ved havnivå. Siden Jorden ikke er en perfekt sfære, er verdiene til g variere litt, være høyere ved polene og lavere ved ekvator.

De som vil vite verdien i lokaliteten deres, kan finne den oppdatert på nettstedet til det tyske metrologiske institutt PTB (Physikalisch-Technische Bundesanstalt), i avsnittet Tyngdekraftsinformasjonssystem (KRITT).

Tyngdekraften på månen

Gravitasjonsfeltet til Månen er bestemt ved å analysere radiosignaler fra romfølere som kretser rundt satellitten. Verdien på måneoverflaten er 1,62 m / s^to

Tyngdekraften på mars

Verdien av g_P for en planet avhenger den av massen M og dens radius R som følger:

Derfor:

For planeten Mars er følgende data tilgjengelig:

M = 6,4185 x 10^{2. 3} kg

R = 3390 km

G = 6,67 x 10^-elleve N.m^to/ kg^to

Med disse dataene vet vi at tyngdekraften til Mars er 3,71 m / s^to. Naturligvis kan den samme ligningen brukes med dataene fra månen eller en hvilken som helst annen planet og dermed estimere verdien av dens tyngdekraft..

Trening løst: det fallende eplet

Anta at både jorden og et eple har sfærisk form. Jordens masse er M = 5,98 x 10²⁴ kg og dens radius er R = 6,37 x 10⁶  m. Massen til eplet er m = 0,10 kg. Anta at det ikke er noen annen kraft enn tyngdekraften. Fra Newtons lov om universell gravitasjon finner du:

a) Gravitasjonskraften som Jorden utøver på eplet.

b) Akselerasjonen som eplet opplever når det frigjøres fra en viss høyde, ifølge Newtons andre lov.

Løsning

a) Eplet (angivelig sfærisk, som jorden) har en veldig liten radius sammenlignet med jordens radius og er nedsenket i gravitasjonsfeltet. Følgende figur er åpenbart ikke i målestokk, men det er et diagram over gravitasjonsfeltet g, og styrken F utøvd av jorden på eplet:

Ved å anvende Newtons lov om universell gravitasjon kan avstanden mellom sentrene betraktes som omtrent den samme verdien som jordens radius (høyden som eplet faller fra er også ubetydelig sammenlignet med jordens radius). Derfor:

b) I henhold til Newtons andre lov er størrelsen på kraften som utøves på eplet:

F = ma = mg

Hvis verdi er 0,983 N, ifølge forrige beregning. Ved å ligne begge verdiene og deretter løse størrelsen på akselerasjonen, får vi:

mg = 0,983 N

g = 0,983 N / 0,10 kg = 9,83 m / s^to

Dette er en veldig god tilnærming til standardverdien av tyngdekraften.

Referanser

1. Giancoli, D. (2006). Fysikk: Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Konseptuell fysikk. Femte utgave. Pearson. 91 - 94.
3. Rex, A. (2011). Grunnleggende om fysikk. Pearson. 213-221.