
Mesh analyse begreper, metoder, eksempler
De nettanalyse er en teknikk som brukes til å løse flate elektriske kretser. Denne prosedyren kan også vises i litteraturen under metodene navnene på kretsstrømmer eller metode for nettstrømmer (eller løkke).
Grunnlaget for denne og andre elektriske kretsanalysemetoder ligger i Kirchhoffs lover og Ohms lov. Kirchhoffs lover er i sin tur uttrykk for to svært viktige prinsipper for bevaring i fysikk for isolerte systemer: både den elektriske ladningen og energien er bevart..

På den ene siden er den elektriske ladningen relatert til strømmen, som er ladningen i bevegelse, mens i en krets er energien koblet til spenningen, som er agenten som har ansvaret for å utføre arbeidet som er nødvendig for å holde ladningen i bevegelse..
Disse lovene, brukt på en flat krets, genererer et sett med samtidige ligninger som må løses for å oppnå strøm- eller spenningsverdiene..
Ligningssystemet kan løses med kjente analytiske teknikker, som f.eks cramer's rule, som krever beregning av determinanter for å få løsningen på systemet.
Avhengig av antall ligninger, løses de ved hjelp av en vitenskapelig kalkulator eller en eller annen matematisk programvare. På nettet er det også mange alternativer tilgjengelig.
Artikkelindeks
- 1 Viktige vilkår
- 2 Metoder
- 2.1 - Trinn for å anvende nettanalyse
- 3 Løst øvelser
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 4 Referanser
Viktige vilkår
Før vi forklarer hvordan det fungerer, begynner vi med å definere disse begrepene:
Gren: seksjon som inneholder et kretselement.
Node: punkt som forbinder to eller flere grener.
Bånd: er en hvilken som helst lukket del av en krets, som starter og slutter ved samme node.
Mesh: sløyfe som ikke inneholder noen annen sløyfe inni (essensielt nett).
Metoder
Mesh analyse er en generell metode som brukes til å løse kretser der elementene er koblet i serie, parallelt eller på en blandet måte, det vil si når forbindelsestypen ikke skiller seg tydelig ut. Kretsen må være flat, eller i det minste må det være mulig å tegne den på nytt som sådan.
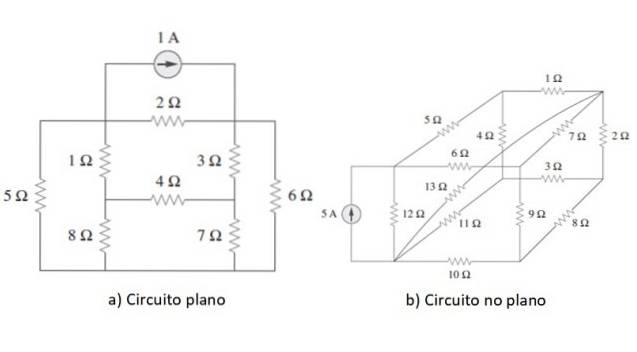
Et eksempel på hver type krets er vist i figuren ovenfor. Når poenget er avklart, vil vi begynne med å bruke metoden på en enkel krets som et eksempel i neste avsnitt, men først vil vi kort gjennomgå lovene til Ohm og Kirchhoff.
Ohms lov: være V spenningen, R motstand e Jeg strømmen til det ohmske resistive elementet, der spenningen og strømmen er direkte proporsjonale, og motstanden er konstant av proporsjonalitet:
V = I.R
Kirchhoffs spenningslov (LKV): I en hvilken som helst lukket bane som kjøres i bare én retning, er den algebraiske summen av spenningene null. Dette inkluderer spenninger på grunn av kilder, motstander, induktorer eller kondensatorer: ∑ E = ∑ RJeg. Jeg
Kirchhoffs gjeldende lov (LKC): på en hvilken som helst node er den algebraiske summen av strømmen null, idet man tar i betraktning at innkommende strømmer tildeles ett tegn og de som forlater et annet. På denne måten: ∑ I = 0.
Med nettstrømmetoden er det ikke nødvendig å anvende Kirchhoffs gjeldende lov, noe som resulterer i færre ligninger å løse.
- Trinn for å anvende nettanalyse
Vi begynner med å forklare metoden for en 2-mesh krets. Prosedyren kan deretter utvides for større kretser.
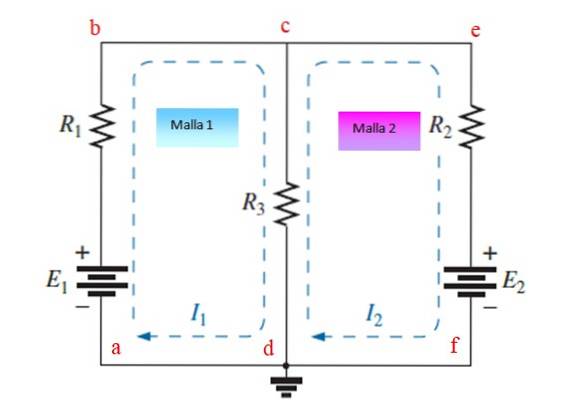
Trinn 1
Tilordne og tegne uavhengige strømmer til hvert maske, i dette eksemplet er de Jeg1 og Jegto. De kan tegnes med eller mot klokken.
Steg 2
Bruk Kirchhoffs lov om spenninger (LTK) og Ohms lov på hvert nett. Potensielle dråper tildeles et tegn (-) mens stiger tildeles et tegn (+).
Mesh abcda
Starter fra punkt a og følger strømens retning, finner vi en potensiell økning i batteri E1 (+), deretter et fall i R1 (-) og deretter en ny dråpe i R3 (-).
Samtidig motstanden R3 blir også krysset av nåværende jegto, men i motsatt retning representerer den derfor en økning (+). Den første ligningen ser slik ut:
OG1-R1.Jeg1 -R3.Jeg1 + R3.Jegto = 0
Deretter faktureres det og vilkårene grupperes på nytt:
- (R1+R3) JEG1 +R3Jegto = -E1 (Ligning 1)
Cefdc mesh
Starter fra poenget og og følger strømens retning, blir et potensielt fall funnet i Rto (-), enda et innfall OGto, siden strømmen kommer inn gjennom + polen på batteriet og til slutt et nytt fall R3 (-), samtidig gjeldende Jeg1 krysser R3 i motsatt retning (+).
Den andre ligningen, med de angitte tegnene, ser slik ut:
- Rto Jegto - OGto -R3 Jegto +R3 Jeg1= 0
R3Jeg1 - (Rto +R3) Jegto = Eto (Ligning 2)
Merk at det er to ligninger med de to ukjente I1 og jegto.
Trinn 3
Systemet med ligninger som således dannes løses deretter.
Løst øvelser
For å begynne med er det viktig å vurdere følgende:
-Sløyfestrøm eller nettstrøm kan tildeles en vilkårlig adresse.
-Hvert essensielt nett - eller "vindu" - som kretsen har, må tildeles en strøm.
-Nettstrømmer er betegnet med en stor bokstav for å skille dem fra strømmer som sirkulerer gjennom grener, selv om strømmen som sirkulerer gjennom en gren i noen tilfeller kan være den samme som for nett.
- Eksempel 1
Finn strømmen som strømmer gjennom hver motstand i kretsen i figur 3, hvis elementene har følgende verdier:
R1 = 20 Ω; Rto = 30 Ω; R3 = 10 Ω; OG1 = 12 V; OGto = 18 V.
Løsning
Først er det nødvendig å tilordne maskeringsstrømmene I1 og jegto og ta ligningssystemet som er utledet i forrige avsnitt, og erstatt deretter verdiene gitt i uttalelsen:
- (R1+R3) JEG1 +R3Jegto = -E1 (Ligning 1)
R3Jeg1 - (Rto +R3) Jegto = Eto (Ligning 2)
-
-(20 + 30) Jeg1 + 10Ito = -12
10I1 - (30 +10) Jegto = 18
--
-femtiJeg1 + 10Ito = -12
10I1 - 40 jegto = 18
Siden det er et ligningssystem på 2 x 2, kan det lett løses ved reduksjon, multiplisere den andre ligningen med 5 for å eliminere det ukjente Jeg1:
-femtiJeg1 + 10 jegto = -12
50I1 - 200 jegto = 90
-
-190 jegto= 78
Jegto = - 78/180 A = - 0,41 A.
Straks tømmes strømmen Jeg1 fra noen av de opprinnelige ligningene:
Jeg1 = (18 + 40 Ito) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A.
Det negative tegnet i strømmen Jegto betyr at strømmen i maske 2 sirkulerer i motsatt retning av den som er trukket.
Strømmene i hver motstand er som følger:
For motstanden R1 strømmen sirkulerer Jeg1 = 0,16 A. i den forstand tegnet av motstand Rto strømmen sirkulerer Jegto = 0,41 A. i motsatt retning av den som er trukket, og av motstanden R3 sirkulere Jeg3 = 0,16- (-0,41) A = 0,57 A. ned.
Systemløsning etter Cramers metode
I matriseform kan systemet løses som følger:
Trinn 1: Beregn Δ

Trinn 2: Beregn Δ1
Den første kolonnen erstattes av de uavhengige vilkårene i ligningssystemet, og opprettholder rekkefølgen systemet ble opprinnelig foreslått:

Trinn 3: Beregn jeg1
Jeg1 = Δ1/ Δ = 300/1900 = 0,16 A
Trinn 4: Beregn Δto

Jegto = Δto/ Δ = -780/1900 = -0,41 A
- Eksempel 2
Bestem strømmen og spenningene gjennom hver motstand i følgende krets, ved hjelp av nettstrømmetoden:

Løsning
De tre maskestrømmene er tegnet, som vist i følgende figur, i vilkårlige retninger. Nå krysses maskene fra hvilket som helst punkt:
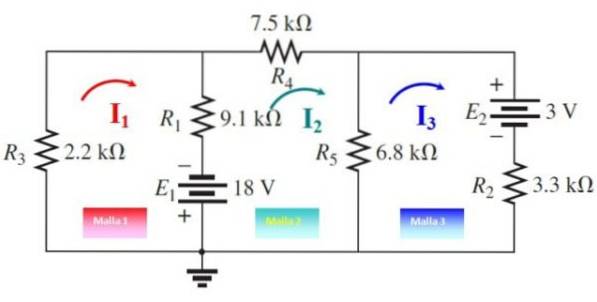
Mask 1
-9100.I1+18-2200.I1+9100.Ito= 0
-11300 I1 + 9100.Ito = -18
Mesh 2
-(7500 + 6800 + 9100) .Ito + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.Ito + 6800.I3 = 18
Mesh 3
-(6800 + 3300) I3 + 6800.Ito - 3 = 0
6800.Ito - 10100.I3 = 3
System av ligninger
-11300 I1 + 9100.Ito + 0.I3= -18
9100.I1 - 23400.Ito + 6800.I3 = 18
0.I1 + 6800.Ito - 10100.I3 = 3
Selv om tallene er store, kan det løses raskt ved hjelp av en vitenskapelig kalkulator. Husk at ligningene må ordnes og legg til nuller på stedene der det ukjente ikke vises, slik det vises her.
Nettstrømmene er:
Jeg1 = 0,0012 A; Jegto = -0.00048 A; Jeg3 = -0.00062 A.
Strømmer Jegto og Jeg3 sirkulere i motsatt retning av det som er vist i figuren, siden de viste seg å være negative.
Tabell over strømmer og spenninger i hver motstand
| Motstand (Ω) | Strøm (ampere) | Spenning = I.R (volt) |
|---|---|---|
| 9100 | Jeg1 -Jegto = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0,00062 | 2,05 |
| 2200 | 0,0012 | 2.64 |
| 7500 | 0,00048 | 3.60 |
| 6800 | Jegto -Jeg3= -0.00048 - (- 0.00062) = 0.00014 | 0,95 |
Cramers regelløsning
Siden de er store, er det praktisk å bruke vitenskapelig notasjon til å jobbe direkte med dem.
Beregning av jeg1
De fargede pilene i 3 x 3 determinanten indikerer hvordan du finner de numeriske verdiene ved å multiplisere de indikerte verdiene. La oss begynne med å få de fra den første braketten i determinanten Δ:
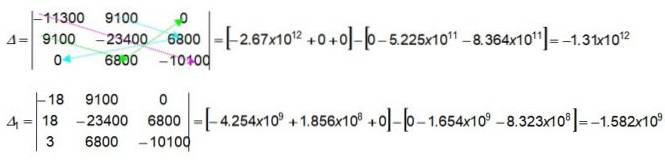
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Umiddelbart får vi den andre braketten i den samme determinanten, som bearbeides fra venstre til høyre (for denne braketten ble de fargede pilene ikke tegnet i figuren). Vi inviterer leseren til å bekrefte det:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10elleve
6800 x 6800 x (-11300) = -5,255 x 10elleve
På samme måte kan leseren også sjekke verdiene for determinanten Δ1.
Viktig: mellom begge parenteser er det alltid et negativt tegn.
Endelig får du strømmen Jeg1 gjennom Jeg1 = Δ1 / Δ
Jeg1 = -1,582 x 109/-1,31 x 1012 = 0,0012 A.
Beregning av jegto
Fremgangsmåten kan gjentas for å beregne Jegto, i dette tilfellet for å beregne determinanten Δto den andre kolonnen til determinanten Δ blir erstattet av kolonnen med de uavhengige begrepene, og verdien er funnet, i henhold til fremgangsmåten som er forklart.
Siden det er tungvint på grunn av det store antallet, spesielt hvis du ikke har en vitenskapelig kalkulator, er det enkleste å erstatte verdien av Jeg1 allerede beregnet, i følgende ligning og klar:
-11300 I1 + 9100.Ito + 0.I3= -18 → 9100 Ito= -18 + 11300 I1 → jegto = -0.00048 A.
Beregning av I3
En gang med verdiene av Jeg1 og Jegto i hånden, den av Jeg3 funnet direkte ved erstatning.
Referanser
- Alexander, C. 2006. Grunnleggende om elektriske kretser. 3.. Utgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduksjon til kretsanalyse.2da. Utgave. Pearson.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 5. Elektrisk interaksjon. Redigert av Douglas Figueroa (USB).
- García, L. 2014. Elektromagnetisme. 2. plass. Utgave. Industrial University of Santander.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 2.



Ingen har kommentert denne artikkelen ennå.