
Aksial belastning hvordan den beregnes og øvelser løses
De aksial belastning Det er kraften som er rettet parallelt med symmetriaksen til et element som utgjør en struktur. Den aksiale kraften eller belastningen kan være strekk eller kompresjon. Hvis aksjonslinjen til aksialkraften sammenfaller med symmetriaksen som passerer gjennom midtpunktet til elementet som blir betraktet, sies det å være en konsentrisk aksial belastning eller kraft.
Tvert imot, hvis det er en aksial kraft eller belastning parallelt med symmetriaksen, men hvis handlingslinje ikke er på selve aksen, er det en eksentrisk aksial kraft.
-
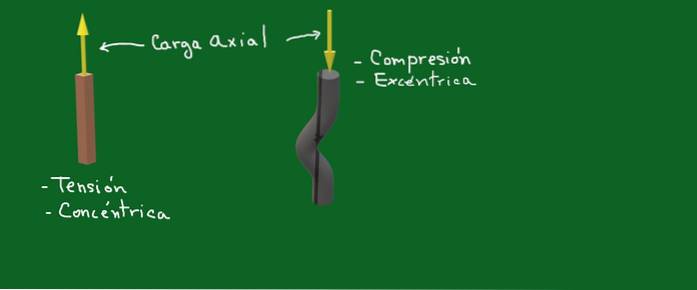
Figur 1. Aksial belastning. Kilde: selvlaget
I figur 1 representerer de gule pilene aksiale krefter eller belastninger. I det ene tilfellet er det en konsentrisk spenningskraft, og i det andre har vi en eksentrisk kompresjonskraft å gjøre.
Måleenheten for aksial belastning i det internasjonale SI-systemet er Newton (N). Men andre kraftenheter som kilo-kraft (kg-f) og pund-kraft (lb-f) brukes også ofte..
Artikkelindeks
- 1 Hvordan beregnes det?
- 1.1 Forholdet mellom aksial belastning og normal belastning
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 3 Referanser
Hvordan beregnes det?
For å beregne verdien av den aksiale belastningen i elementene i en struktur, må følgende trinn følges:
- Lag kraftdiagrammet på hvert element.
- Bruk ligningene som garanterer translasjonell likevekt, det vil si at summen av alle krefter er null.
- Tenk på ligningen av dreiemomenter eller momenter slik at rotasjonsvekt er oppfylt. I dette tilfellet må summen av alle momentene være null.
- Beregn kreftene, samt identifiser kreftene eller aksiale belastningene i hvert av elementene.
Forholdet mellom aksial belastning og normal belastning
Gjennomsnittlig normal belastning er definert som forholdet mellom aksial belastning delt på tverrsnittsareal. Enhetene til normal innsats i International System S.I. de er Newton over kvadratmeter (N / m²) eller Pascal (Pa). Følgende figur 2 illustrerer begrepet normal stress for klarhet..
-
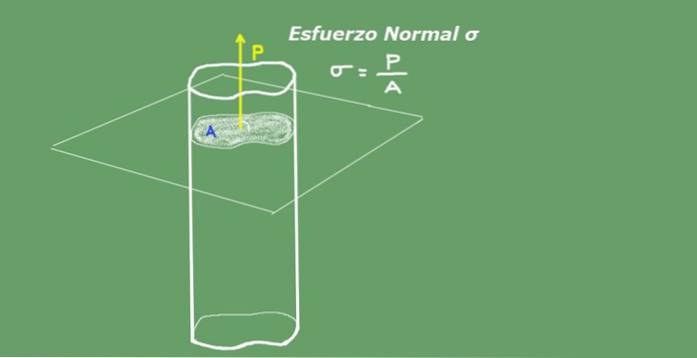
Figur 2. Normal stress. Kilde: selvlaget.
Løst øvelser
-Øvelse 1
Tenk på en sylindrisk betongsøyle med høyde h og radius r. Anta at tettheten av betong er ρ. Kolonnen bærer ikke annen ekstra belastning enn sin egen vekt og støttes på en rektangulær base.
- Finn verdien av aksial belastning ved punktene A, B, C og D, som er i følgende posisjoner: A ved bunnen av søylen, B a ⅓ av høyden h, C a ⅔ av høyden h og etter siste D ved toppen av kolonnen.
- Bestem også gjennomsnittlig normal belastning ved hver av disse posisjonene. Ta følgende tallverdier: h = 3m, r = 20cm og ρ = 2250 kg / m³
-
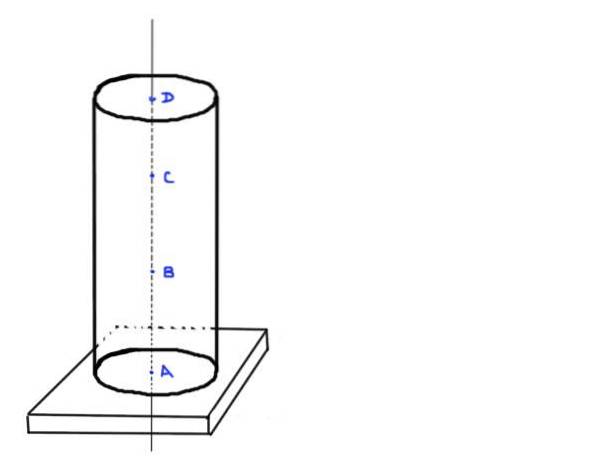
Figur 3. Sylindrisk kolonne. Kilde: selvlaget.
Løsning
Total kolonnevekt
Den totale vekten W av kolonnen er produktet av dens tetthet ganger volumet multiplisert med tyngdeakselerasjonen:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Aksial belastning i A
Ved punkt A må kolonnen bære sin fulle vekt, så aksial belastning på dette punktet er kompresjon er lik vekten til kolonnen:
PA = W = 8313 N
Aksial belastning ved B
Bare ⅔ av kolonnen vil være på punkt B, så den aksiale belastningen på dette punktet vil være kompresjon og verdien ⅔ vekten til kolonnen:
PB = ⅔ W = 5542 N
Figur 3. Sylindrisk kolonne. Kilde: selvlaget.
Over posisjon C er det bare ⅓ av kolonnen, så dens aksialkompresjonsbelastning vil være ⅓ av sin egen vekt:
PC = ⅓ W = 2771 N
Aksial belastning i D
Til slutt er det ingen belastning på punkt D, som er den øvre enden av kolonnen, så den aksiale kraften på det punktet er null..
PD = 0 N
Normal innsats i hver av stillingene
For å bestemme normal spenning i hver av posisjonene vil det være nødvendig å beregne tverrsnittet av område A, gitt av:
A = π ∙ r² = 0,126 m²
På denne måten vil den normale spenningen i hver av posisjonene være kvotienten mellom den aksiale kraften i hvert av punktene delt på det allerede beregnede tverrsnittsarealet, som i denne øvelsen er det samme for alle punkter fordi det er en kolonne sylindrisk.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Øvelse 2
Figuren viser en struktur som består av to søyler som vi vil kalle AB og CB. Stang AB støttes i enden A av en stift og i den andre enden er den forbundet med den andre stangen av en annen stift B.
Tilsvarende støttes stangen CB ved enden C ved hjelp av en tapp og i enden B med tappen B som forbinder den med den andre stangen. En vertikal kraft eller belastning F påføres pin B som vist i følgende figur:
-
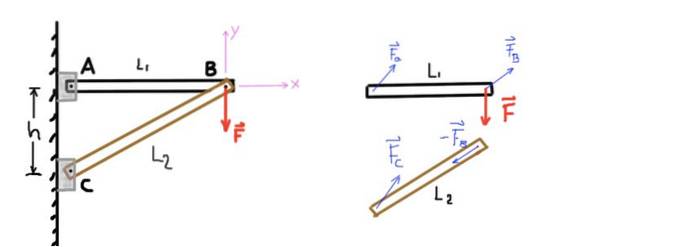
Figur 4. To-stolpes struktur og fritt kroppsdiagram. Kilde: selvlaget.
Anta at vekten til stolpene er ubetydelig, siden kraften F = 500 kg-f er mye større enn vekten av strukturen. Skillet mellom støtter A og C er h = 1,5 m og lengden på stangen AB er L1 = 2 m. Bestem den aksiale belastningen på hver av stolpene, og indiker om det er kompresjon eller aksial belastning.
Løsning 2
Figuren viser, ved hjelp av et frikroppsdiagram, kreftene som virker på hvert av elementene i strukturen. Det kartesiske koordinatsystemet som styrke-likevektsligningene vil bli etablert med, er også indikert..
Dreiemomenter eller momenter vil bli beregnet ved punkt B og vil bli betraktet som positive hvis de peker bort fra skjermen (Z-aksen). Balansen mellom krefter og dreiemoment for hver stang er:
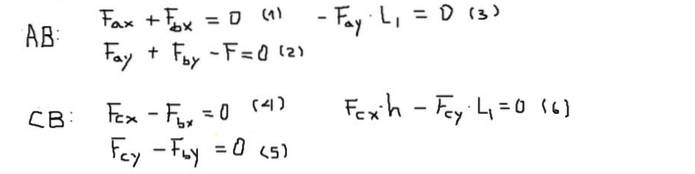
Deretter løses komponentene av kreftene til hver av ligningene i følgende rekkefølge:
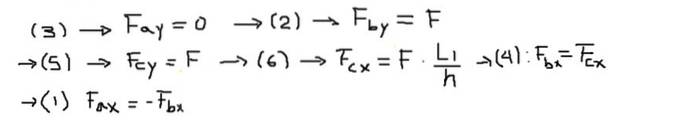
Til slutt beregnes de resulterende kreftene i endene av hver stolpe:
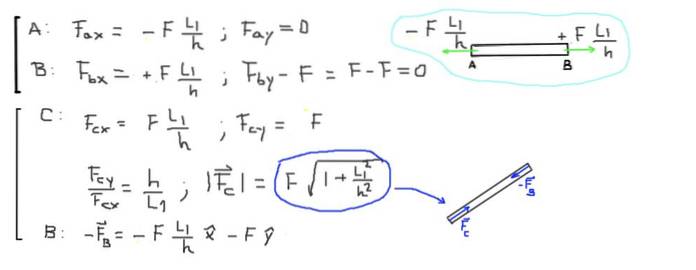
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
Stangen CB er i kompresjon på grunn av de to kreftene som virker i endene som er parallelle med stangen og peker mot sentrum. Størrelsen på den aksiale kompresjonskraften i stangen CB er:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Referanser
- Øl F ... Mekanikk av materialer. 5. Utgave. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Materialmekanikk. Åttende utgave. Prentice Hall. 2011. 3-60.
- Gere J. Mekanikk av materialer. Åttende utgave. Cengage læring. 4-220.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. 6. utg. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Notater om generell fysikk. UNAM. 87-98.



Ingen har kommentert denne artikkelen ennå.