De korrelasjonskoeffisient i statistikk er det en indikator som måler tendensen til to kvantitative variabler X og Y til å ha et lineært eller proporsjonalt forhold mellom seg.
Generelt er parene med variabler X og Y to kjennetegn ved samme populasjon. For eksempel kan X være en persons høyde og Y sin vekt..
I dette tilfellet vil korrelasjonskoeffisienten indikere om det er en trend mot et proporsjonalt forhold mellom høyde og vekt i en gitt populasjon..
Pearsons lineære korrelasjonskoeffisient er angitt med bokstaven r små bokstaver og minimums- og maksimumsverdiene er henholdsvis -1 og +1.
En verdi r = +1 vil indikere at settet med par (X, Y) er perfekt justert, og at når X vokser, vil Y vokse i samme proporsjon. På den annen side, hvis det skjedde at r = -1, ville settet med par også være perfekt justert, men i dette tilfellet når X øker, reduseres Y i samme andel.
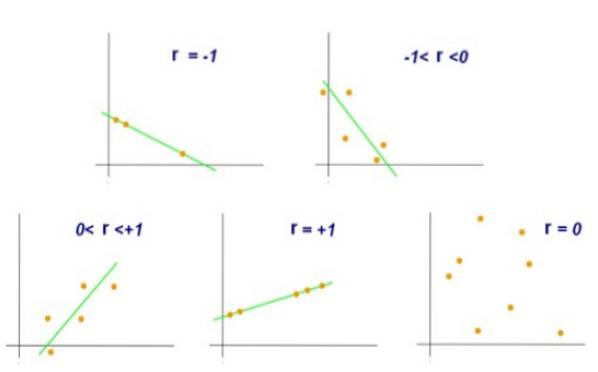
På den annen side vil en verdi på r = 0 indikere at det ikke er noen lineær korrelasjon mellom variablene X og Y. Mens en verdi på r = +0.8 vil indikere at parene (X, Y) har en tendens til å klynges på den ene siden og en annen av en viss straight.
Formelen for å beregne korrelasjonskoeffisienten r er som følger:
Den lineære korrelasjonskoeffisienten er en statistisk størrelse som finnes i vitenskapelige kalkulatorer, de fleste regneark og statistiske programmer..
Det er imidlertid praktisk å vite hvordan formelen som definerer den brukes, og for dette vil en detaljert beregning vises, utført på et lite datasett.
Og som det ble sagt i forrige avsnitt, er korrelasjonskoeffisienten kovariansen Sxy delt på produktet av standardavviket Sx for variablene X og Sy for variabelen Y.
Kovariansen Sxy er:
Sxy = [Σ (Xi -
Hvor summen går fra 1 til N datapar (Xi, Yi).
For sin del er standardavviket for variabelen X kvadratroten til variansen til datasettet Xi, med i fra 1 til N:
Sx = √ [Σ (Xi -
Tilsvarende er standardavviket for variabelen Y kvadratroten til variansen til datasettet Yi, med i fra 1 til N:
Sy = √ [Σ (Yi -
For å vise detaljert hvordan man beregner korrelasjonskoeffisienten, tar vi følgende sett med fire datapar
(X, Y): (1, 1); (2. 3); (3, 6) og (4, 7).
Først beregner vi det aritmetiske gjennomsnittet for X og Y, som følger:
Deretter beregnes de resterende parametrene:
Sxy = [(1 - 2,5) (1 - 4,25) + (2 - 2,5) (3 - 4,25) + (3 - 2,5) (6 - 4,25) +….…. (4 - 2,5) (7 - 4,25) ] / (4-1)
Sxy = [(-1,5) (- 3,25) + (-0,5) (- 1,25) + (0,5) (1,75) + ... .
…. (1.5) (2.75)] / (3) = 10.5 / 3 = 3.5
Sx = √ [(-1,5)to + (-0,5)to + (0,5)to + (1.5)to) / (4-1)] = √ [5/3] = 1.29
Sx = √ [(-3,25)to + (-1,25)to + (1,75)to + (2,75)to) / (4-1)] =
√ [22.75 / 3] = 2,75
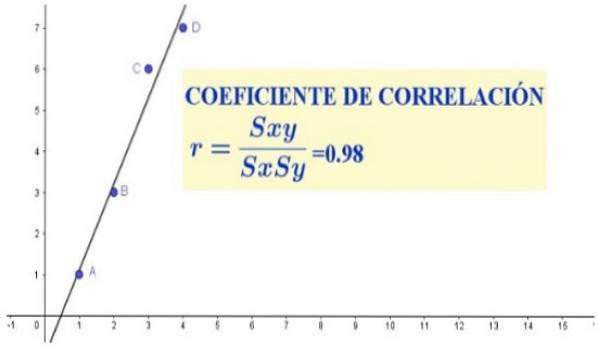
r = 3,5 / (1,29 * 2,75) = 0,98
I datasettet i forrige tilfelle observeres en sterk lineær korrelasjon mellom variablene X og Y, som manifesteres både i spredningsdiagrammet (vist i figur 1) og i korrelasjonskoeffisienten, som ga en verdi ganske nær enhet.
I den grad korrelasjonskoeffisienten er nærmere 1 eller -1, desto mer fornuftig er det å tilpasse dataene til en linje, resultatet av lineær regresjon..
Den lineære regresjonslinjen er hentet fra Metode for minste firkanter. der parametrene til regresjonslinjen er oppnådd fra minimering av summen av kvadratet av differansen mellom den estimerte Y-verdien og Yi av N-dataene.
På den annen side er parametrene a og b for regresjonslinjen y = a + bx, oppnådd ved metoden med minste kvadrat,:
* b = Sxy / (Sxto) For skråningen
* a =
Husk at Sxy er kovariansen definert ovenfor og Sxto er variansen eller kvadratet til standardavviket som er definert ovenfor.
Korrelasjonskoeffisienten brukes til å bestemme om det er en lineær korrelasjon mellom to variabler. Det er aktuelt når variablene som skal studeres er kvantitative, og videre antas det at de følger en normal typefordeling..
Vi har et illustrerende eksempel nedenfor: et mål på graden av fedme er kroppsmasseindeksen, som oppnås ved å dele vekten til en person i kilogram med høyden i samme kvadrat i enheter kvadratmeter.
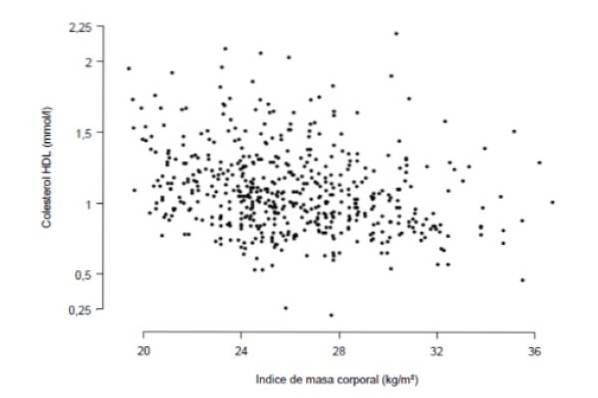
Du vil vite om det er en sterk sammenheng mellom kroppsmasseindeksen og konsentrasjonen av HDL-kolesterol i blodet, målt i millimol per liter. For dette formålet er det utført en studie med 533 personer, som er oppsummert i følgende graf, der hvert punkt representerer dataene til en person.
Nøye observasjon av grafen viser at det er en viss lineær trend (ikke veldig markert) mellom konsentrasjonen av HDL-kolesterol og kroppsmasseindeksen. Det kvantitative målet på denne trenden er korrelasjonskoeffisienten, som i dette tilfellet viste seg å være r = -0,276.
Ingen har kommentert denne artikkelen ennå.