De enhetssirkel er en sirkel med radius lik 1, som vanligvis er sentrert på punktet (0,0) i det kartesiske koordinatsystemet xy. Brukes til å enkelt definere de trigonometriske forholdene til vinkler ved hjelp av riktige trekanter.
Ligningen til enhetssirkelen sentrert ved opprinnelsen er:
xto + Yto = 1
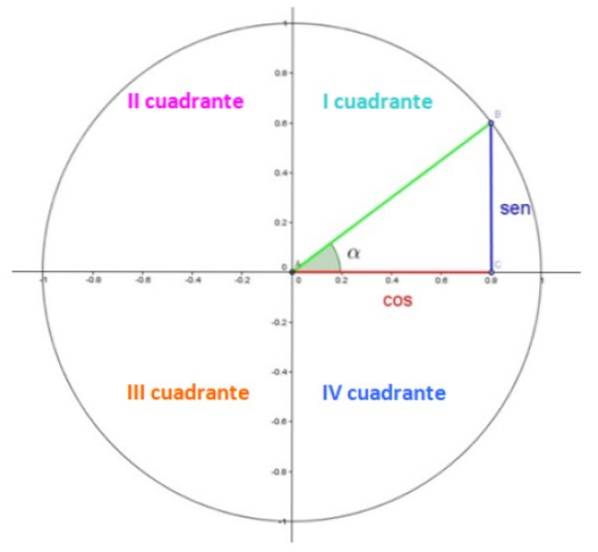
I figur 1 har vi enhetssirkelen, der hvert kvartal er i en kvadrant. Kvadranter er nummerert med romertall og telles mot klokken.
I den første kvadranten er det en trekant. Bena, i rødt og blått, måler henholdsvis 0,8 og 0,6, mens hypotenusen i grønt måler 1, siden det er en radius.
Den spisse vinkelen α er en sentral vinkel i standardposisjon, noe som betyr at toppunktet sammenfaller med punktet (0,0) og den første siden med den positive x-aksen. Vinkelen måles mot klokken og tildeles et positivt tegn etter konvensjon.
Vel, i enhetssirkelen er cosinus- og sinuskoordinatene til α henholdsvis x- og y-koordinatene til punkt B, som i eksemplet vist er 0,8 og 0,6.
Fra disse to defineres de:
Artikkelindeks
Hvis vi begrenser oss til rette trekanter, vil de trigonometriske forholdene bare gjelde akutte vinkler. Men ved hjelp av enhetssirkelen utvides beregningen av de trigonometriske forholdene til enhver vinkel α.
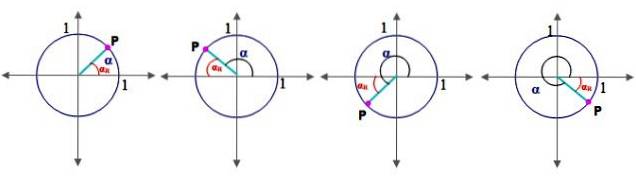
For dette er det nødvendig å først definere begrepet referansevinkel αR:
La α være en vinkel i standardposisjon (den hvis startsiden sammenfaller med den positive x-aksen), dens referansevinkel αR er mellom hans terminal side og x-aksen. Figur 2 viser referansevinkelen for vinkler i kvadrat I, II, III og IV.
For hver kvadrant beregnes referansevinkelen slik:
-Første kvadrant: αR = α
-Andre kvadrant: αR = 180º - α
-Tredje kvadrant: αR = α - 180º
-Fjerde kvadrant: αR = 360º - α
Merk at den første kvadranten vinkelen α sammenfaller med referansevinkelen. Vel, de trigonometriske forholdene til vinkelen α er de samme som referansevinkelen, med tegnene i henhold til kvadrantene der den endelige siden av α faller..
Med andre ord sammenfaller de trigonometriske cosinus- og sinusforholdene til vinkelen α med koordinatene til punktet P, ifølge figur 2.
I den følgende figuren ser vi de trigonometriske forholdene til noen bemerkelsesverdige vinkler, som er utledet fra enhetssirkelen.
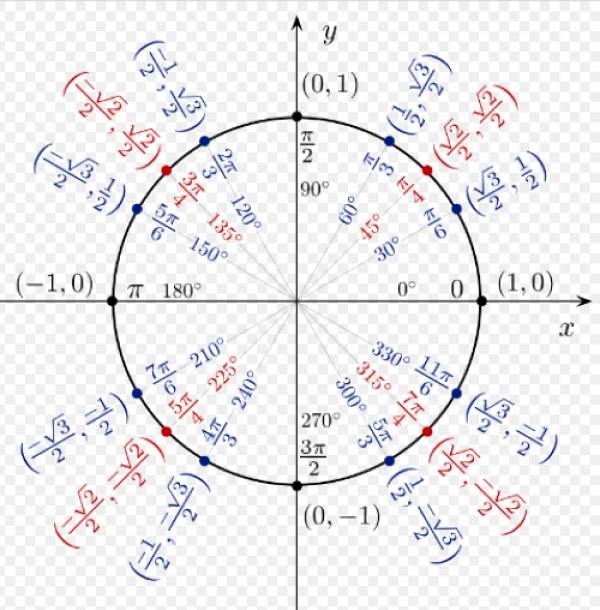
Forholdet mellom cosinus og sinus i hvilken som helst vinkel i I-kvadranten er alle positive. For α = 60º har vi koordinatene (1/2; √3 / 2), som tilsvarer henholdsvis cos 60º og sin 60º.
Koordinatene til α = 120º er (-1/2; √3 / 2), siden x-koordinaten er i den andre kvadranten, er negativ.
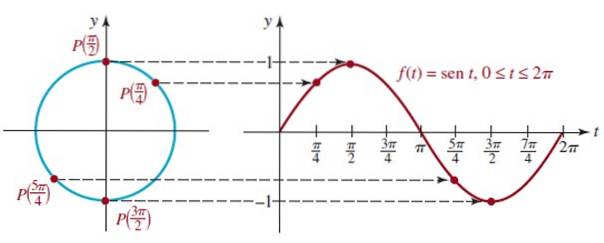
Ved hjelp av enhetssirkelen og koordinatene til punktene P på den er det mulig å tegne grafene til funksjonene cos t og sin t, som vi vil se nedenfor.
For å gjøre dette er forskjellige posisjoner av punktet P (t) plassert på enhetssirkelen. Vi begynner med grafen til funksjonen f (t) = sin t.
Vi kan se at når vi går fra t = 0 til t = π / 2 (90º), øker verdien av sin t til den når 1, som er den maksimale verdien.
På den annen side, fra t = π / 2 til t = 3π / 2 synker verdien av sin t fra 1, og går gjennom 0 ved t = π til den når sitt minimum -1 ved t = 3π / 2.
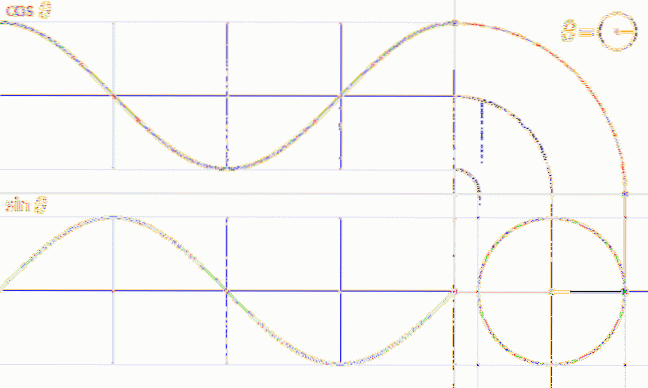
Figuren viser grafen til den første syklusen av f (t) = sin t som tilsvarer den første runden av enhetssirkelen, denne funksjonen er periodisk med periode 2π.
En analog prosedyre kan utføres for å få grafen til funksjonen f (t) = cos t, som vist i følgende animasjon:
-Begge funksjonene er kontinuerlige i settet med reelle tall og også periodiske, fra periode 2π.
-Domenet til funksjonene f (t) = sin t og f (t) = cos t er alle reelle tall: (-∞, ∞).
-For området eller banen til sinus og cosinus har vi intervallet [-1,1]. Parantesene indikerer at -1 og 1 er inkludert.
- Nullene til sin t er verdiene som tilsvarer nπ med n heltall, mens nullene til cos t er [(2n + 1) / 2] med n også heltall.
-Funksjonen f (t) = sin t er merkelig, den har symmetri om opprinnelsen mens funksjonen cos t er jevn, symmetrien handler om den vertikale aksen.
Gitt cos t = - 2/5, som er den horisontale koordinaten til punktet P (t) på enhetssirkelen i den andre kvadranten, få den tilsvarende vertikale koordinaten sin t.
Siden P (t) tilhører enhetssirkelen, der det er sant at:
xto + Yto = 1
Derfor:
y = ± √ 1 - xto
Siden P (t) er i andre kvadrant, vil den positive verdien tas. Den vertikale koordinaten til punktet P (t) er y:
y = √ 1 - (-2/5)to = √0,84
En matematisk modell for temperatur T i grader Fahrenheit på en gitt dag, t timer etter midnatt, er det gitt av:
T (t) = 50 + 10 sin [(π / 12) × (t - 8)]
Med t mellom 0 og 24 timer. Finne:
a) Temperaturen klokka 8.00.
b) Timer der T (t) = 60ºF
c) Maksimums- og minimumstemperaturer.
Vi erstatter t = 8 i den gitte funksjonen:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x sin 0 = 50 ºF
50 + 10 sin [(π / 12) × (t-8)] = 60
Det er en trigonometrisk ligning, og vi må løse for det ukjente "t":
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
Vi vet at sin π / 2 = 1, derfor må sinusargumentet være 1:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 timer
Det konkluderes med at temperaturen er 14 ° C etter 14.00, det vil si 14.00. Det er ingen annen tid i løpet av dagen (24 timer) når dette skjer.
Maksimumstemperaturen tilsvarer verdien der sin [(π / 12) × (t-8)] = 1 og er 60 ºF. På den annen side oppstår minimum hvis sin [(π / 12) × (t-8)] = -1 og er 40ºF.
Ingen har kommentert denne artikkelen ennå.