Stiv kropp

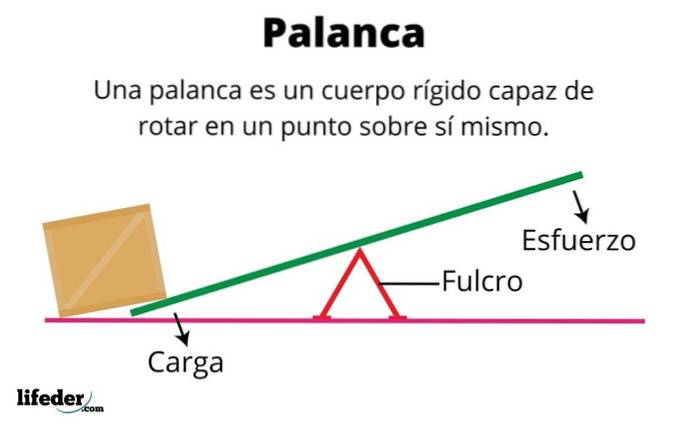
Hva er en stiv kropp?

En stiv kropp er en materiell gjenstand hvis partikler alltid forblir i de samme relative posisjonene. Derfor er det et objekt som ikke deformeres, en kvalitet som tilskrives de sterke kohesjonskreftene som holder partiklene på plass..

I virkeligheten har partiklene i ethvert legeme som utsettes for ytre krefter en tendens til å vibrere eller bevege seg, så objektet deformeres alltid til en viss grad, men disse effektene er vanligvis små.

Når dette er tilfelle, kan det antas at kroppen er stiv og har en veldig god tilnærming til sin oppførsel, selv om det er en idealisering.

Stive kroppstyper

Det kan skilles mellom to typer stive karosserier:

• De som har partikler i diskrete mengder, det vil si at de kan telles. For eksempel kan to metallkuler forbundet med en tynn og lett stang betraktes som en enkelt enhet. Hvis stangen er stiv nok til ikke å bøyes, betraktes systemet som en stiv kropp.
• De som er kontinuerlige, noe som betyr at partiklene som utgjør dem, ikke kan skilles fra hverandre. Hverdagslige gjenstander og natur er gode eksempler: steiner, møbler og andre, så vel som jorden og andre steinete himmellegemer.

Stiv kroppsbevegelse og dynamikk

I likhet med gjenstander som blir sett på som partikler, kan stive kropper oversettes, rotere og ha en mer generell bevegelse, kombinere oversettelse og rotasjon.

For å studere oversettelsen er det ikke nødvendig å analysere bevegelsen til hver partikkel separat, men heller bevegelsen av massesenteret, et punkt der det anses at all massen til objektet er konsentrert..

Disse translasjons- og rotasjonsbevegelsene kan være:

• Uavhengig, som i tilfelle planeter, som har en rotasjonsbevegelse rundt sin akse (regnes som fast) og en oversettelsesbevegelse rundt solen, men hastighetene til hver er ikke relatert..
• Roto-oversettelse, hvis vinkelhastigheten og translasjonshastigheten til massesenteret er relatert. I dette tilfellet er rotasjonsaksen mobil, som i tilfellet med sylinderen som ruller nedover en bratt skråning uten å skli..

Dynamikken til den stive kroppen

Følgende mengder er relevante i dynamikken til den stive kroppen:

Massesenter

Massesenteret er det punktet der hele kroppens masse anses å være konsentrert. Hvis det er en homogen og symmetrisk kropp, for eksempel en kule, faller massesenteret sammen med det geometriske sentrum.

Treghetsmoment

Denne skalære størrelsen er verdien av rotasjonsinerti eller motstand som et objekt motvirker for å rotere rundt en bestemt akse. Det avhenger helt av objektets geometri og dens masse, og derfor er det i visse tilfeller lettere å rotere rundt bestemte akser enn andre..

For legemer med veldefinerte geometriske former er det tabeller med treghetsmomenter med hensyn til symmetriaksene, for eksempel den som passerer gjennom massesenteret. Med denne informasjonen og setningene knyttet til treghetsmomentet, kan øyeblikkene om andre akser enkelt beregnes..

Krefter og dreiemoment eller dreiemoment

Det tar krefter å bevege en kropp. Hvis massesenteret til det stive faste stoffet blir oversatt, er bevegelsesligningen, ifølge Newtons andre lov:

F_nett = M ∙til_cm

Hvor:

-Nettokraften er F_nett

-M er massen

-Akselerasjonen av massesenteret er til_cm

Imidlertid lykkes ikke alle de påførte kreftene med å få objektet til å rotere. Dette krever dreiemoment eller dreiemoment, som forteller hvor effektiv rotasjonsvirkningen til en kraft er. Det er definert som vektorproduktet mellom posisjonsvektoren r med hensyn til et visst punkt O og kraften F i spørsmålet. Det er betegnet med det greske brevet τ (i fet skrift, da det også er en vektor):

τ = r × F

I SI International System er enheten for dreiemoment N⋅m (newton per meter).

I mange tilfeller er rotasjonsbevegelse rundt en akse gjennom massesenteret beskrevet av en ligning analog til Newtons andre lov:

Kinetisk energi av et stivt fast stoff

Bevegelsen til et stivt legeme er beskrevet av oversettelser av massesenteret og rotasjonene rundt det punktet, derfor har dets kinetiske energi begge bidrag.

La K være kroppens kinetiske energi, v_cm hastigheten til massesenteret, M kroppens masse, I_cm dens treghetsmoment om massesenteret og ω vinkelhastigheten. Det kan vises at den kinetiske energien er:

K = ½ Mv_cm^to + ½ jeg_cm ω^to

Det observeres at det andre begrepet til høyre er rotasjonsanalogen til begrepet til venstre. Der spiller treghetsmomentet den samme rollen som massen, mens vinkelhastigheten har samme rolle som den lineære hastigheten..

Eksempler i hverdagen

Fysisk pendel

Den fysiske pendelen eller den virkelige pendelen er veldig enkel å bygge: den består av et stivt fast stoff, for eksempel en stang eller stang, som svinger fritt rundt en horisontal akse. Rotasjonsaksen passerer ikke gjennom objektets massesenter, og dette kan i prinsippet ha noen form.

Denne pendelen skiller seg fra den enkle pendelen, fordi i sistnevnte anses massen som komponerer den å være punktlig.

Sykkelhjul

Et annet eksempel på et velkjent stivt karosseri er sykkelhjulet, hvis akse går gjennom massesenteret, som går gjennom midten av hjulet. Så lenge den ikke lener seg til den ene siden eller snur, gjelder dynamikklikningene beskrevet ovenfor for å beskrive bevegelsen..

En bowlingkule

Stiv solid modell er godt egnet til å beskrive bowlingkulebevegelser på banen eller når du ruller uten å gli ned på returrampen.

Yoyo

Dette populære leketøyet er laget av en sylinder av tre eller plast og en streng viklet i et spor som omgir det..

Sylinderen kan modelleres som et stivt legeme der spenningen i strengen gir dreiemomentet for svingen, mens vekten (påført massesenteret) og spenningen er ansvarlig for den vertikale akselerasjonen av massesenteret..

Referanser

1. Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 
2. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
3.  Katz, D. 2013. Fysikk for forskere og ingeniører. Fundamenter og forbindelser. Cengage læring.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1. Pearson.
5. Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.