Raskt kan det være kjent hva er skillelinjene på 30, så vel som ethvert annet tall (annet enn null), men den grunnleggende ideen er å lære hvordan divisorene til et tall beregnes på en generell måte.
Det må utvises forsiktighet når man snakker om delere, fordi det raskt kan fastslås at alle delere på 30 er 1, 2, 3, 5, 6, 10, 15 og 30, men hva med det negative ved disse tallene? Er de skillelinjer eller ikke?
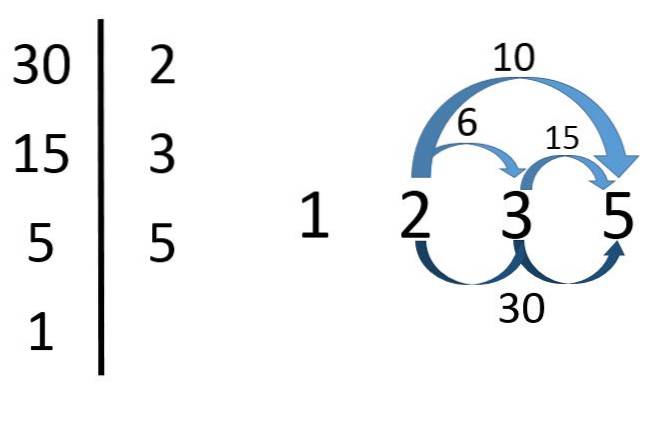
For å svare på det forrige spørsmålet er det nødvendig å forstå et veldig viktig begrep i matematikkens verden: divisjonsalgoritmen.
Inndelingsalgoritmen (eller euklidisk inndeling) sier følgende: gitt to heltall "n" og "b", hvor "b" er forskjellig fra null (b ≠ 0), er det bare heltall "q" og "r", slik at n = bq + r, hvor 0 ≤ r < |b|.
Tallet "n" kalles et utbytte, "b" kalles en divisor, "q" kalles et kvotient og "r" kalles resten eller resten. Når resten "r" er lik 0, sies det at "b" deler "n", og dette betegnes med "b | n".
Inndelingsalgoritmen er ikke begrenset til positive verdier. Derfor kan et negativt tall være en deler av et annet tall.
Ved å bruke divisjonsalgoritmen kan man se at 30 = 7,5 × 4 + 0. Resten er lik null, men det kan ikke sies at 7,5 deler med 30 fordi når vi snakker om delere, snakker vi bare om hele tall.
Som man kan se på bildet, for å finne delerne på 30, må dens viktigste faktorer først bli funnet.
Så, 30 = 2x3x5. Fra dette konkluderer vi med at 2, 3 og 5 er delere på 30. Men det er også produktene fra disse viktigste faktorene.
Så 2 × 3 = 6, 2 × 5 = 10, 3 × 5 = 15, og 2x3x5 = 30 er delere på 30. Den 1 er også en divisor på 30 (selv om den faktisk er en divisor av hvilket som helst tall).
Det kan konkluderes med at 1, 2, 3, 5, 6, 10, 15 og 30 er delere på 30 (alle overholder divisjonsalgoritmen), men det må huskes at deres negative også er delere.
Derfor er alle delere av 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 og 30.
Det som er lært ovenfor kan brukes på et hvilket som helst heltall.
For eksempel, hvis du vil beregne delere på 92, fortsett som før. Nedbrytes som et produkt av primtall.
Del 92 med 2 og få 46; del nå 46 med 2 igjen og få 23.
Dette siste resultatet er et primtall, så det vil ikke ha flere delere foruten 1 og samme 23.
Vi kan da skrive 92 = 2x2x23. Fremgangsmåten som før, blir det konkludert med at 1,2,4,46 og 92 er delere av 92.
Til slutt er negativene til disse tallene inkludert i den forrige listen, som listen over alle delere på 92 er -92, -46, -4, -2, -1, 1, 2, 4, 46, 92.
Ingen har kommentert denne artikkelen ennå.