
Triangle inequality demonstration, eksempler, løste øvelser
Det kalles ulikhet i trekanten til egenskapen til to reelle tall som består i at den absolutte verdien av summen deres alltid er mindre enn eller lik summen av deres absolutte verdier. Denne egenskapen er også kjent som Minkowski ulikhet eller trekantet ulikhet.
Denne egenskapen til tall kalles triangulær ulikhet fordi det i trekanter hender at lengden på den ene siden alltid er mindre enn eller lik summen av de to andre, selv om denne ulikheten ikke alltid gjelder i området med trekanter..

Det er flere bevis på den trekantede ulikheten i reelle tall, men i dette tilfellet vil vi velge en basert på egenskapene til absolutt verdi og binomialet i kvadrat.
Teorem: For hvert par tall til Y b knyttet til de reelle tallene, må den:
| a + b | ≤ | til | + | b |
Artikkelindeks
- 1 Demo
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 2.4 Eksempel 4
- 2.5 Eksempel 5
- 2.6 Eksempel 6
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 3.4 Øvelse 4
- 4 Referanser
Demonstrasjon
Vi begynner med å vurdere det første medlemmet av ulikheten, som vil være kvadratisk:
| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (lik. 1)
I forrige trinn brukte vi egenskapen at et hvilket som helst tall i kvadrat er lik den absolutte verdien til det nevnte tallet i kvadrat, det vil si: | x | ^ 2 = x ^ 2. Utviklingen av det kvadratiske binomialet har også blitt brukt.
Alt nummer x er mindre enn eller lik sin absolutte verdi. Hvis tallet er positivt, er det likt, men hvis tallet er negativt, vil det alltid være mindre enn et positivt tall. I dette tilfellet sin egen absolutte verdi, det vil si at det kan sies at x ≤ | x |.
Produktet (a b) er et tall, derfor gjelder det at (a b) ≤ | a b |. Når denne egenskapen brukes på (likning 1) har vi:
| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | a b | + b ^ 2 (likning 2)
Tatt i betraktning det | a b | = | a || b | (Likning 2) kan skrives som følger:
| a + b | ^ 2 ≤ a ^ 2 + 2 | a || b | + b ^ 2 (likning 3)
Men siden vi tidligere sa at kvadratet til et tall er lik den absolutte verdien av tallet i kvadrat, kan ligning 3 skrives om som følger:
| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (likning 4)
I det andre medlemmet av ulikheten anerkjennes et bemerkelsesverdig produkt, som når det påføres fører til:
| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (likning 5)
I det forrige uttrykket skal det bemerkes at verdiene som skal kvadreres i begge medlemmene av ulikheten, er positive, derfor må det også tilfredsstilles at:
| a + b | ≤ (| a | + | b |) (likning 6)
Ovennevnte uttrykk er akkurat det man ønsket å demonstrere.
Eksempler
Deretter vil vi sjekke den trekantede ulikheten med flere eksempler.
Eksempel 1
Vi tar verdien a = 2 og verdien b = 5, det vil si begge positive tall, og vi sjekker om ulikheten er oppfylt eller ikke.
| 2 + 5 | ≤ | 2 | + | 5 |
| 7 | ≤ | 2 | + | 5 |
7 ≤ 2+ 5
Likhet er verifisert, derfor er trekant-ulikhetssetningen oppfylt.
Eksempel 2
Følgende verdier er valgt a = 2 og b = -5, det vil si et positivt tall og det andre negative, vi sjekker om ulikheten er oppfylt eller ikke.
| 2 - 5 | ≤ | 2 | + | -5 |
| -3 | ≤ | 2 | + | -5 |
3 ≤ 2 + 5
Ulikheten er oppfylt, derfor er den trekantede ulikhetssetningen bekreftet.
Eksempel 3
Vi tar verdien a = -2 og verdien b = 5, det vil si et negativt tall og den andre positive, vi sjekker om ulikheten er oppfylt eller ikke.
| -2 + 5 | ≤ | -2 | + | 5 |
| 3 | ≤ | -2 | + | 5 |
3 ≤ 2 + 5
Ulikheten er bekreftet, derfor er teoremet oppfylt.
Eksempel 4
Følgende verdier er valgt a = -2 og b = -5, det vil si begge negative tall, og vi sjekker om ulikheten er oppfylt eller ikke.
| -2 - 5 | ≤ | -2 | + | -5 |
| -7 | ≤ | -2 | + | -5 |
7 ≤ 2+ 5
Likhet er verifisert, derfor er Minkowskis ulikhetssetning oppfylt.
Eksempel 5
Vi tar verdien a = 0 og verdien b = 5, det vil si et tall null og den andre positive, så sjekker vi om ulikheten er oppfylt eller ikke.
| 0 + 5 | ≤ | 0 | + | 5 |
| 5 | ≤ | 0 | + | 5 |
5 ≤ 0+ 5
Likhet er oppfylt, derfor er trekant-ulikhetssetningen bekreftet.
Eksempel 6
Vi tar verdien a = 0 og verdien b = -7, det vil si et tall null og den andre positive, så sjekker vi om ulikheten er oppfylt eller ikke.
| 0 - 7 | ≤ | 0 | + | -7 |
| -7 | ≤ | 0 | + | -7 |
7 ≤ 0+ 7
Likhet er bekreftet, derfor er den trekantede ulikhetssetningen oppfylt.
Løst øvelser
I de følgende øvelsene representerer du geometrisk trekantulikheten eller Minkowski-ulikheten for tallene a og b.
Tallet a vil bli representert som et segment på X-aksen, dets opprinnelse O sammenfaller med null på X-aksen og den andre enden av segmentet (ved punkt P) vil være i den positive retningen (til høyre) av X-akse hvis a> 0, men hvis a < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
På samme måte vil tallet b bli representert som et segment med opprinnelse på punkt P. Den andre ekstreme, det vil si punkt Q vil være til høyre for P hvis b er positiv (b> 0) og punkt Q vil være | b | enheter til venstre for P hvis b<0.
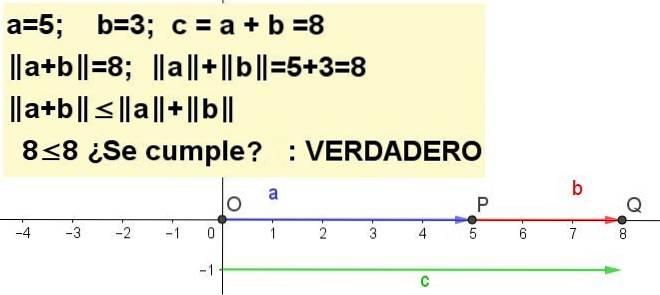
Øvelse 1
Graf trekant ulikhet for a = 5 og b = 3 | a + b | ≤ | til | + | b |, å være c = a + b.
Øvelse 2
Graf den trekantede ulikheten for a = 5 og b = -3.
| a + b | ≤ | til | + | b |, å være c = a + b.

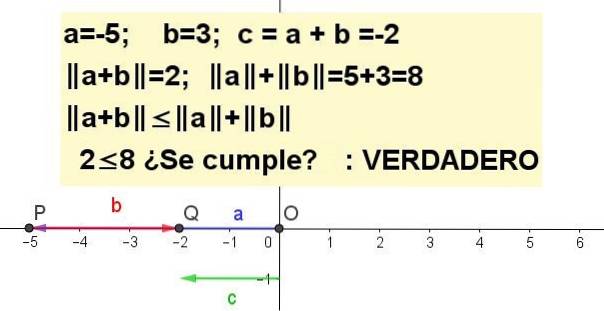
Øvelse 3
Vis grafisk ulikhet for a = -5 og b = 3.
| a + b | ≤ | til | + | b |, å være c = a + b.
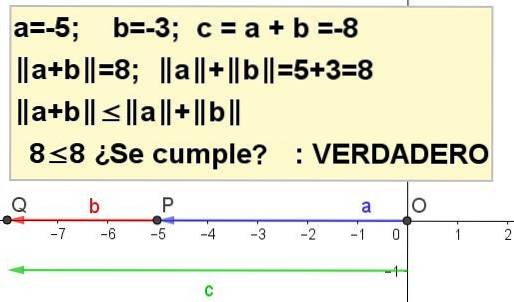
Øvelse 4
Konstruer grafisk den trekantede ulikheten for a = -5 og b = -3.
| a + b | ≤ | til | + | b |, å være c = a + b.
Referanser
- E. Whitesitt. (1980). Boolsk algebra og dens applikasjoner. Redaksjonsselskap Continental C. A.
- Mícheál O 'Searcoid. (2003) Elements of Abstract Analysis ... Institutt for matematikk. Høgskolen i Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Matematikk og ingeniørfag i informatikk. Institutt for informatikk og teknologi. National Bureau of Standards. Washington, D.C. 20234
- Eric Lehman. Matematikk for informatikk. Google Inc..
- F Thomson Leighton (1980). Kalkulus. Institutt for matematikk og datalogi og AI-laboratorium, Massachusetts Institute of Technology.
- Khan Academy. Triangle Inequality Theorem. Gjenopprettet fra: khanacademy.org
- Wikipedia. Trekantet ulikhet. Gjenopprettet fra: es. wikipedia.com



Ingen har kommentert denne artikkelen ennå.