De lineær utvidelse oppstår når et objekt opplever ekspansjon på grunn av en variasjon i temperatur, hovedsakelig i en dimensjon. Dette skyldes materialets egenskaper eller dens geometriske form..
For eksempel i en ledning eller en stang, når det er en økning i temperaturen, er det lengden som lider den største endringen på grunn av termisk utvidelse..
Kablene som fuglene i forrige figur abborer på, får en strekk når temperaturen øker; i stedet trekker de seg sammen når de avkjøles. Det samme skjer for eksempel med stengene som danner skinnene til en jernbane.
Artikkelindeks
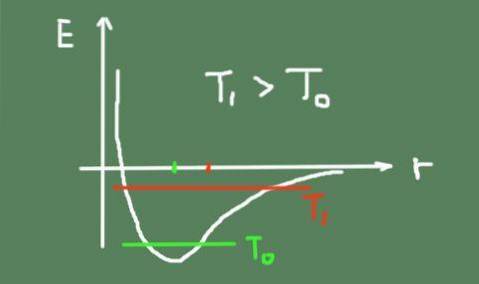
I et fast materiale opprettholder atomene sine relative posisjoner mer eller mindre faste rundt et likevektspunkt. På grunn av termisk omrøring svinger de imidlertid alltid rundt det samme.
Når temperaturen øker, øker også den termiske svingningen, noe som får de midterste svingningsposisjonene til å endres. Dette er fordi bindingspotensialet ikke er akkurat parabolsk og har asymmetri rundt minimum.
Nedenfor er en figur som skisserer den kjemiske bindingsenergien som en funksjon av den interatomiske avstanden. Den viser også den totale svingningsenergien ved to temperaturer, og hvordan svingningssenteret beveger seg.
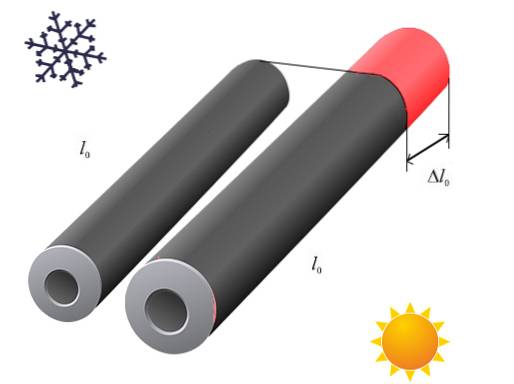
For å måle lineær ekspansjon, begynner vi med en startlengde L og en starttemperatur T, av objektet hvis ekspansjon skal måles..
Anta at dette objektet er en stang med lengden L og tverrsnittsdimensjonene er mye mindre enn L.
Dette objektet blir først utsatt for en temperaturvariasjon AT, slik at den endelige temperaturen til objektet når den termiske likevekten med varmekilden er etablert vil være T '= T + AT.
Under denne prosessen vil objektets lengde også ha endret seg til en ny verdi L '= L + ΔL, der ΔL er variasjonen i lengden.
Koeffisienten for lineær ekspansjon α er definert som kvotienten mellom den relative variasjonen i lengde per enhetsvariasjon i temperatur. Følgende formel definerer koeffisienten for lineær ekspansjon α:
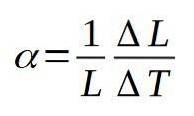
Dimensjonene til koeffisienten for lineær utvidelse er dimensjonene for temperaturen.
Deretter vil vi gi en liste over koeffisienten for lineær ekspansjon for noen typiske materialer og elementer. Koeffisienten beregnes ved normalt atmosfæretrykk basert på en omgivelsestemperatur på 25 ° C; og dens verdi betraktes som konstant i et AT-område på opptil 100 ° C.
Enheten til koeffisienten for lineær ekspansjon vil være (° C)-1.
- Stål: α = 12 ∙ 10-6 (° C)-1
- Aluminium: α = 23 ∙ 10-6 (° C)-1
- Gull: α = 14 ∙ 10-6 (° C)-1
- Kobber: α = 17 ∙ 10-6 (° C)-1
- Messing: α = 18 ∙ 10-6 (° C)-1
- Jern: α = 12 ∙ 10-6 (° C)-1
- Glass: α = (7 til 9) ∙ 10-6 (° C)-1
- Kvikksølv: α = 60,4 ∙ 10-6 (° C)-1
- Kvarts: α = 0,4 ∙ 10-6 (° C)-1
- Diamant: α = 1,2 ∙ 10-6 (° C)-1
- Bly: α = 30 ∙ 10-6 (° C)-1
- Eiketre: α = 54 ∙ 10-6 (° C)-1
- PVC: α = 52 ∙ 10-6 (° C)-1
- Karbonfiber: α = -0,8 ∙ 10-6 (° C)-1
- Betong: α = (8 til 12) ∙ 10-6 (° C)-1
De fleste materialer strekker seg med temperaturøkning. Imidlertid krymper noen spesielle materialer som karbonfiber med økende temperatur..
En kobberkabel henges mellom to poler, og lengden på en kjølig dag ved 20 ° C er 12 m. Beregn verdien på lengdegraden på en varm dag ved 35 ° C.
Ut fra definisjonen av koeffisienten for lineær ekspansjon, og å vite at for kobber er denne koeffisienten lik: α = 17 ∙ 10-6 (° C)-1
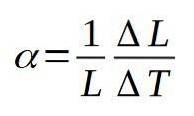
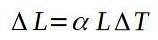
Kobberkabelen gjennomgår en økning i lengden, men dette er bare 3 mm. Det vil si at kabelen går fra å ha 12 000 m til å ha 12 003 m.
I en smie går en aluminiumsstang ut av ovnen ved 800 grader Celsius, og måler en lengde på 10,00 m. Når den er avkjølt til romtemperaturen på 18 grader Celsius, må du bestemme hvor lang stangen vil være.
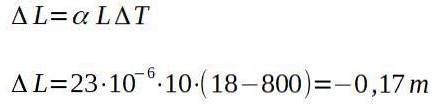
Med andre ord vil stangen, når den er kald, ha en total lengde på:
9,83 moh.
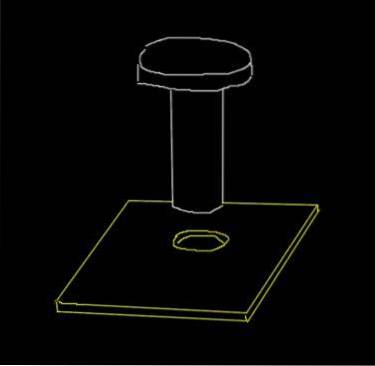
En stålnitte har en diameter på 0,915 cm. På en aluminiumsplate er det laget et hull på 0,910 cm. Dette er de innledende diametrene når omgivelsestemperaturen er 18 ° C.
Til hvilken minimumstemperatur må platen varmes opp for at naglen skal passere gjennom hullet? Målet med dette er at når strykejernet går tilbake til romtemperatur, vil naglen sitte tett i platen.
Selv om platen er en overflate, er vi interessert i utvidelsen av hullets diameter, som er en endimensjonal størrelse..
La oss ringe D0 til den opprinnelige diameteren på aluminiumsplaten, og D som den en gang vil være oppvarmet til.
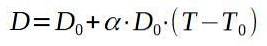
Å løse den endelige temperaturen T, har vi:
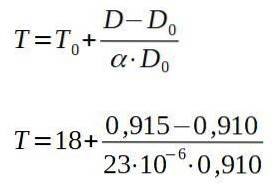
Resultatet av de forrige operasjonene er 257 ° C, som er minimumstemperaturen som platen må varmes opp til slik at naglen passerer gjennom hullet.
Niten og platen fra forrige øvelse plasseres sammen i en ovn. Bestem hvilken minimumstemperatur ovnen må ha for at stålnitten skal passere gjennom hullet i aluminiumsplaten.
I dette tilfellet vil både naglen og hullet utvides. Men utvidelseskoeffisienten til stål er α = 12 ∙ 10-6 (° C)-1, mens aluminium er α = 23 ∙ 10-6 (° C)-1 .
Vi ser da etter en endelig temperatur T slik at begge diametre sammenfaller.
Hvis vi kaller naglen 1 og aluminiumsplaten 2, ser vi etter en endelig temperatur T slik at D1 = Dto.
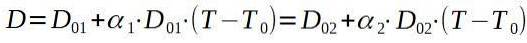
Hvis vi løser den endelige temperaturen T, sitter vi igjen med:
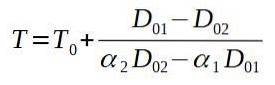
Så setter vi de tilsvarende verdiene.
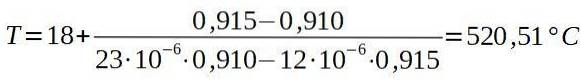
Konklusjonen er at ovnen må være minst 520,5 ° C for at naglen skal passere gjennom hullet i aluminiumsplaten.
Ingen har kommentert denne artikkelen ennå.