Eneagon egenskaper, hvordan lage en eneagon, eksempler

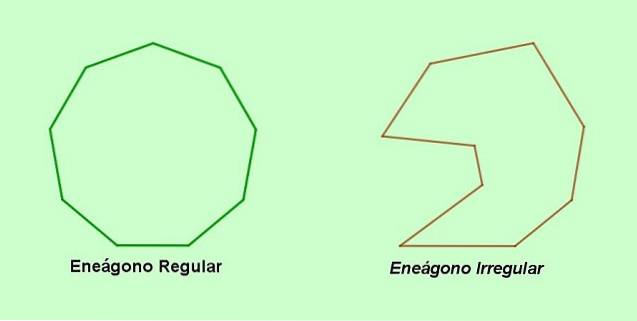
EN eneagon er en polygon med ni sider og ni hjørner, som kanskje eller ikke kan være vanlige. Navnet eneágono kommer fra gresk og består av de greske ordene ennea (ni og gonon (vinkel).

Et alternativt navn for den ni-sidige polygonen er nonagon, et ord som kommer fra latin nonus (ni og gonon (toppunkt). På den annen side, hvis sidene eller vinklene til enegonen er ulik hverandre, så har vi en uregelmessig enegon. Hvis derimot de ni sidene og de ni vinklene til enegonen er like, er det a vanlig enegon.

Artikkelindeks

• 1 Egenskaper for enegon
  • 1.1 Vanlig enegon
  • 1.2 Område av enegon som er kjent siden og apotemet
  • 1.3 Område av en kjent enegon på siden
  • 1.4 Omkretsen til den vanlige enegonen kjente sin side
  • 1,5 Enegonens omkrets kjent sin radius
• 2 Hvordan lage en vanlig eneagon
• 3 eksempler
  • 3.1 Eksempel 1
  • 3.2 Eksempel 2
• 4 Referanser

Eneagon egenskaper

For en polygon med n sider er summen av de indre vinklene:

(n - 2) * 180º

I enegonen ville det være n = 9, så summen av de indre vinklene er:

Sa = (9 - 2) * 180º = 7 * 180º = 1260º

I en hvilken som helst polygon er antall diagonaler:

D = n (n - 3) / 2 og når det gjelder enegon, siden n = 9, har vi da at D = 27.

Vanlig enegon

I den vanlige eneagon eller nonagon er det ni (9) indre vinkler med like mål, derfor måler hver vinkel en niende av den totale summen av de indre vinklene.

Målingen på enegons indre vinkler er da 1260º / 9 = 140º.

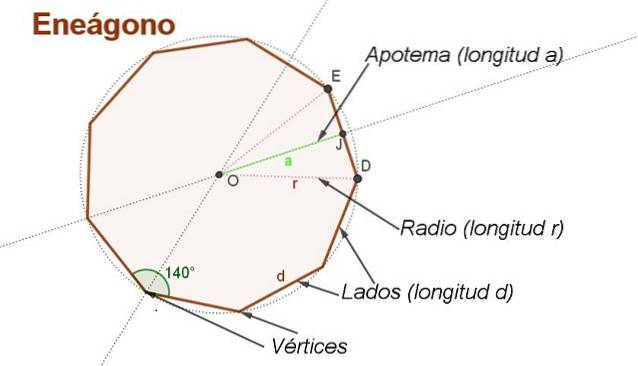
Å utlede formelen for området til en vanlig enegon med side d det er praktisk å lage noen hjelpekonstruksjoner, som vist i figur 2.

Senteret ligger ELLER spore halveringslinjene på to tilstøtende sider. Senteret ELLER like langt fra hjørner.

En lengderadius r er segmentet som går fra sentrum ELLER til toppunktet i enegonen. Radiene er vist i figur 2. OD Y OE av lengde r.

Apotemet er segmentet som går fra sentrum til midtpunktet på den ene siden av enegonen. For eksempel OJ er et apotem hvis lengde er til.

Område av en kjent enegon siden og apotemet

Vi vurderer trekanten ODE på figur 2. Arealet av denne trekanten er produktet av basen FRA for høyden OJ delt på 2:

Område ODE = (DE * OJ) / 2 = (d * a) / 2

Siden det er 9 trekanter med like areal i enegonen, konkluderes det med at området av det samme er:

Eneagon-området = (9/2) (d * a)

Område av en kjent enegon på siden

Hvis bare lengden d på sidene av enegonen er kjent, er det nødvendig å finne lengden på apotemet for å kunne bruke formelen fra forrige avsnitt.

Vi vurderer trekanten ØYE rektangel i J (se figur 2). Hvis det tangentielle trigonometriske forholdet blir brukt, får vi:

så(∡OEJ) = OJ / Eks.

Vinkelen ∡OEJ = 140º / 2 = 70º, å være EO halvsnitt av den indre vinkelen på enegonen.

På den andre siden, OJ er apothem av lengde til.

Så som J er midtpunktet for ED det følger at EJ = d / 2.

Å erstatte de tidligere verdiene i den tangentrelasjonen vi har:

brunfarget (70º) = a / (d / 2).

Nå fjerner vi lengden på apotemet:

a = (d / 2) brunfarget (70º).

Det forrige resultatet er erstattet i områdeformelen for å oppnå:

Eneagon-området = (9/2) (d * a) = (9/2)( d * (d / 2) brunfarget (70º)

Til slutt finner vi formelen som gjør det mulig å oppnå arealet til den vanlige enegonen hvis bare lengden er kjent d fra sidene:

Eneagon-området = (9/4) d^to brunfarge (70º) = 6.1818 d^to

Perimeter av vanlig enegon kjente sin side

Omkretsen til en polygon er summen av sidene. Når det gjelder enegon, måler hver og en av sidene en lengde d, omkretsen vil være summen av ni ganger d, nemlig:

Omkrets = 9 d

Enegonens omkrets kjente sin radius

Tatt i betraktning trekanten ØYE rektangel i J (se figur 2), brukes det trigonometriske cosinusforholdet:

cos (∡OEJ) = Eks / OE = (d / 2) / r

Hvor er det hentet fra:

d = 2r cos (70º)

Ved å erstatte dette resultatet får vi formelen for omkretsen som en funksjon av enegonens radius:

Omkrets = 9 d = 18 r cos (70º) = 6.1564 r

Hvordan lage en vanlig eneagon

1 - For å bygge en vanlig eneagon, med en linjal og et kompass, start fra omkretsen c som avgrenser enegonen. (se figur 3)

2- To vinkelrette linjer er tegnet gjennom sentrum O av omkretsen. Deretter er kryssene A og B på en av linjene merket med omkretsen.

3- Med kompasset sentrert ved skjæringspunktet B og åpningen lik radiusen BO, tegnes en bue som avskjærer den opprinnelige omkretsen ved et punkt C.

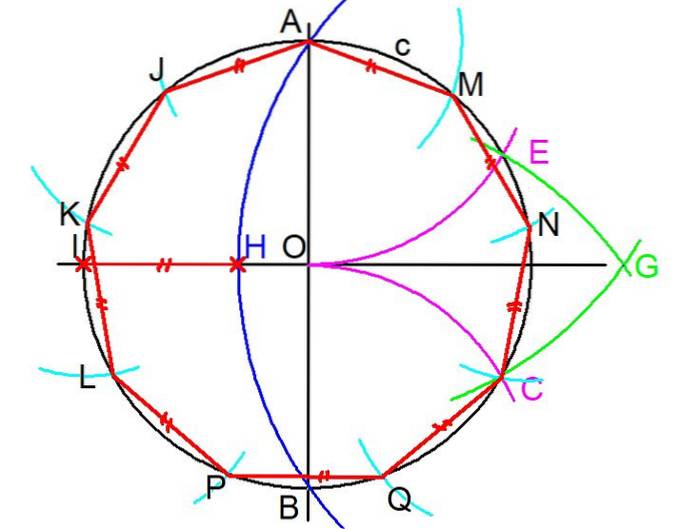
4- Det forrige trinnet gjentas, men ved å lage et senter ved A og radius AO, tegnes en bue som avskjærer omkretsen c ved punkt E.

5- Med vekselstrøm og senter i A tegnes en omkretsbue. Tilsvarende med åpning BE og sentrum B tegnes en annen bue. Krysset mellom disse to buene er markert som punkt G.

6- Sentrering ved G og åpning GA, tegnes en bue som avskjærer sekundæraksen (horisontalt i dette tilfellet) ved punkt H. Krysset mellom sekundæraksen og den opprinnelige omkretsen c er markert som I.

7- Lengden på segmentet IH er lik lengden d på siden av enegonen.

8- Med kompassåpning IH = d trekkes buene i sentrum A radius AJ, sentrum J radius AK, sentrum K radius KL og sentrum L radius LP suksessivt.

9- På samme måte, startende fra A og fra høyre side, tegnes buer med radius IH = d som markerer punktene M, N, C og Q på den opprinnelige omkretsen c.

10- Endelig tegnes segmentene AJ, JK, KL, LP, AM, MN, NC, CQ og til slutt PB.

Det skal bemerkes at konstruksjonsmetoden ikke er helt nøyaktig, siden det kan verifiseres at den siste siden PB er 0,7% lengre enn de andre sidene. Til dags dato er det ingen kjent konstruksjonsmetode med en linjal og kompass som er 100% nøyaktig..

Eksempler

Her er noen eksempler.

Eksempel 1

Du vil bygge en vanlig enegon hvis sider måler 2 cm. Hvilken radius må ha omkretsen som omgir den, slik at når man bruker konstruksjonen beskrevet tidligere, oppnås ønsket resultat?

Løsning:

I et forrige avsnitt ble formelen som relaterer radius r av den omskrevne sirkelen med siden d av en vanlig enegon utledet:

d = 2r cos (70º)

Å løse for r fra forrige uttrykk har vi:

r = d / (2 cos (70º)) = 1,4619 * d

Ved å erstatte verdien d = 2 cm i den forrige formelen, oppnås en radius r på 2,92 cm.

Eksempel 2

Hva er arealet til en vanlig enegon med en side på 2 cm?

Løsning:

For å svare på dette spørsmålet, må vi referere til formelen, som er vist tidligere, som lar oss finne området til en kjent enegon etter lengden d på siden:

Eneagon-området = (9/4) d^to brunfarge (70º) = 6.1818 d^to

Ved å erstatte d for verdien på 2 cm i forrige formel, får vi:

Eneagon-området = 24,72 cm

Referanser

1. C. E. A. (2003). Element av geometri: med øvelser og geometri av kompasset. University of Medellin.
2. Campos, F., Cerecedo, F. J. (2014). Matematikk 2. Grupo Editorial Patria.
3. Freed, K. (2007). Oppdag polygoner. Referanseutdanningsfirma.
4. Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
5. IGER. (s.f.). Matematikk Første semester Tacaná. IGER.
6. Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
7. Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende utgave). Pearson Education.
8. Patiño, M. (2006). Matematikk 5. Redaksjonell Progreso.