
Gravitasjonsenergiformler, egenskaper, applikasjoner, øvelser
De gravitasjonsenergi Det er den som en massiv gjenstand har når den er nedsenket i gravitasjonsfeltet produsert av en annen. Noen eksempler på gjenstander med gravitasjonsenergi er: eplet i treet, det fallende eplet, månen som kretser rundt jorden og jorden som kretser rundt solen.
Isaac Newton (1642-1727) var den første til å innse at tyngdekraften er et universelt fenomen og at hvert objekt med masse i omgivelsene produserer et felt som er i stand til å produsere en kraft på en annen.

Artikkelindeks
- 1 Formler og ligninger
- 2 Kjennetegn ved gravitasjonsenergi
- 2.1 Gravitasjonsfelt og potensial
- 3 applikasjoner
- 3.1 Jordens gravitasjonspotensiale
- 3.2 Potensiell energi nær jordoverflaten
- 4 Øvelser
- 4.1 Øvelse 1: Jordens gravitasjonskollaps
- 4.2 Øvelse 2: Gravitasjonskollaps og unnslippshastighet
- 4.3 Øvelse 3: Gravitasjonsenergien til eplet
- 5 Referanser
Formler og ligninger
Kraften Newton refererte til er kjent som gravitasjonskraften og gir energi til objektet som den virker på. Newton formulerte loven om universell gravitasjon som følger:
"La det være to punktobjekter med henholdsvis massene m1 og m2, hver utøver en attraktiv kraft på den andre som er proporsjonal med massenes produkt og omvendt proporsjonal med kvadratet på avstanden som skiller dem.".
Gravitasjonsenergi ELLER assosiert med gravitasjonskraft F Det er:

Et objekt som er nedsenket i et gravitasjonsfelt har gravitasjonspotensial energi ELLER og kinetisk energi K. Hvis det ikke er andre interaksjoner, eller de har ubetydelig intensitet, er den totale energien OG av nevnte objekt er summen av dens gravitasjonsenergi pluss dens kinetiske energi:
E = K + U
Hvis et objekt er i et gravitasjonsfelt og ingen andre dissipative krefter er tilstede, for eksempel friksjon eller luftmotstand, så er den totale energien OG er en mengde som forblir konstant under bevegelse.
Kjennetegn ved gravitasjonsenergi
- Et objekt har gravitasjonspotensialenergi hvis det bare er i nærvær av gravitasjonsfeltet produsert av et annet.
- Gravitasjonsenergien mellom to objekter øker ettersom skilleavstanden mellom dem er større.
- Arbeidet utført av gravitasjonskraften er lik og i motsetning til variasjonen av gravitasjonsenergien til den endelige posisjonen i forhold til den i sin opprinnelige posisjon..
- Hvis et legeme bare utsettes for tyngdekraften, er variasjonen av dens gravitasjonsenergi lik og i motsetning til variasjonen av dets kinetiske energi..
- Den potensielle energien til et masseobjekt m som er i en høyde h med hensyn til jordoverflaten er mgh ganger større enn den potensielle energien på overflaten, blir g tyngdeakselerasjonen, for høyder h mye mindre enn jordradien.
Gravitasjonsfelt og potensial
Gravitasjonsfeltet g er definert som gravitasjonskraften F per enhetsmasse. Den bestemmes ved å plassere en testpartikkel m ved hvert punkt i rommet og beregne kvotienten mellom kraften som virker på testpartikkelen delt på verdien av massen:
g = F / m
Gravitasjonspotensialet V for et objekt med masse m er definert som gravitasjonspotensialenergien til det objektet delt på sin egen masse.
Fordelen med denne definisjonen er at gravitasjonspotensialet bare avhenger av gravitasjonsfeltet, slik at når potensialet er kjent V, gravitasjonsenergi ELLER av et masseobjekt m Det er:
U = m.V

applikasjoner
Gravitasjonspotensial energi er den som lagres av legemer når de befinner seg i et gravitasjonsfelt.
For eksempel har vannet i en tank mer energi ettersom tanken er høyere..
Jo høyere tankhøyden er, jo større er hastigheten på vannet som forlater kranen. Dette skyldes det faktum at den potensielle energien til vannet i høyden på tanken blir transformert til kinetisk energi til vannet ved utløpet av kranen..
Når vannet er oppdemmet på toppen av et fjell, kan potensiell energi utnyttes for å snu kraftproduksjonsturbiner..
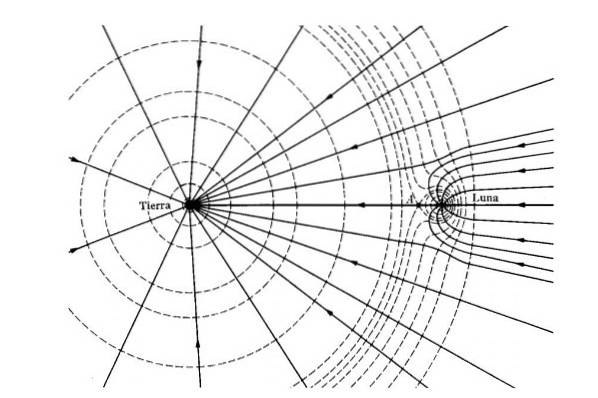
Gravitasjonsenergi forklarer også tidevannet. Siden energien og gravitasjonskraften er avhengig av avstand, er gravitasjonstrekket til Månen større på overflaten av jorden nærmest månen enn ansiktet lengst og motsatt..
Dette gir en forskjell i krefter som deformerer havoverflaten. Effekten er større i en nymåne når solen og månen er justert.
Muligheten for å bygge romstasjoner og satellitter som forblir relativt nær planeten vår skyldes gravitasjonsenergi produsert av jorden. Ellers ville romstasjoner og kunstige satellitter streife gjennom rommet.
Jordens gravitasjonspotensiale
Anta at jorden har masse M og en gjenstand som er over jordoverflaten i det fjerne r med hensyn til sentrum av det har masse m.
I dette tilfellet bestemmes gravitasjonspotensialet ut fra gravitasjonsenergien bare ved å dele på massen til objektet som resulterer:

Potensiell energi nær jordoverflaten
Anta at jorden har en radius RT og masse M.
Selv om jorden ikke er et punktobjekt, tilsvarer feltet på overflaten det som ville blitt oppnådd hvis all dens masse M ble konsentrert i sentrum, slik at gravitasjonsenergien til et objekt i høyden h over jordoverflaten er
U (RT + h) = -G.M m (RT + h) ^ - 1
Men fordi h er mye mindre enn RT, Ovennevnte uttrykk kan tilnærmes med
U = Uo + mgh
Hvor g er tyngdeakselerasjonen, hvis gjennomsnittsverdi for jorden er 9,81 m / s ^ 2.
Da er den potensielle energien Ep til et objekt med masse m i høyden h over jordoverflaten:
Ep (h) = U + Uo = mgh
På jordoverflaten h = 0, så et objekt på overflaten har Ep = 0. Detaljerte beregninger kan sees i figur 3.

Opplæring
Øvelse 1: Jordens gravitasjonskollaps
Anta at planeten vår lider av et gravitasjonskollaps på grunn av tap av termisk energi i sitt indre, og at radiusen faller til halvparten av den nåværende verdien, men massen på planeten forblir konstant..
Bestem hva tyngdekraften akselererer nær overflaten til New Earth og hvor mye en overlevende som veier 50 kg-f vil veie før kollaps. Øk eller reduser gravitasjonsenergien til personen og med hvilken faktor.
Løsning
Akselerasjonen av tyngdekraften på overflaten til en planet avhenger av dens masse og dens radius. Gravitasjonskonstanten er universell og fungerer likt for planeter og exoplaneter.
I dette tilfellet, hvis jordens radius reduseres med halvparten, vil tyngdekraften til den nye jorden være fire ganger større. Detaljer kan sees på følgende tavle.

Dette betyr at en supermann og overlevende som veide 50 kg-f på den gamle planeten, vil veie 200 kg-f på den nye planeten..
På den annen side vil gravitasjonsenergien ha blitt halvert på overflaten til den nye planeten..
Øvelse 2: Gravitasjonssammenbrudd og unnslippe hastighet
I referanse til situasjonen presentert i oppgave 1, hva som ville skje med rømningshastigheten: den øker, avtar, med hvilken faktor?
Løsning 2
Rømningshastighet er den minste hastigheten som er nødvendig for å unnslippe tyngdekraften til en planet.
For å beregne det antas det at et prosjektil som avfyres med denne hastigheten når uendelig med null hastighet. Videre er gravitasjonsenergien ved uendelig null. Derfor vil et prosjektil som fyres med rømningshastighet ha total total energi.
Med andre ord, på overflaten av planeten på tidspunktet for skuddet, må summen av den kinetiske energien til prosjektilet + gravitasjonsenergien være null:
½ m Ve ^ 2 - (G M.m) / RT = 0
Merk at rømningshastigheten ikke avhenger av prosjektilets masse og verdien i kvadrat er
Ve ^ 2 = (2G M) / R.T
Hvis planeten kollapser til en radius halvparten av originalen, blir firkanten til den nye rømningshastigheten dobbelt.
Derfor vokser den nye rømningshastigheten og blir 1,41 ganger den gamle rømningshastigheten:
Gå '= 1,41 Gå
Øvelse 3: Gravitasjonsenergien til eplet
En gutt på balkongen i en bygning 30 meter over bakken slipper et 250 g eple, som etter noen sekunder når bakken.

a) Hva er gravitasjonsenergiforskjellen til eplet øverst i forhold til eplet på bakkenivå?
b) Hvor raskt var eplet like før det sølte på bakken?
c) Hva skjer med energien når eplet er flat ut mot bakken?
Løsning
a) Gravitasjonsenergiforskjellen er
m.g.h = 0,250 kg * 9,81 m / s ^ 2 * 30 m = 73,6 J
b) Den potensielle energien som eplet hadde da det var 30 m høyt, blir transformert til kinetisk energi når eplet når bakken.
½ m v ^ 2 = m.g.h
v ^ 2 = 2.g.h
Ved å erstatte verdier og løse følger det at eplet når bakken med en hastighet på 24,3 m / s = 87,3 km / t.
c) Åpenbart er spredt og all gravitasjonsenergi som er akkumulert i begynnelsen, går tapt i form av varme, siden eplebitene og innvirkningssonen blir oppvarmet, i tillegg blir en del av energien også spredt i form av lyd bølger "spruter".
Referanser
- Alonso, M. (1970). Physics Vol. 1, Inter-American Educational Fund.
- Hewitt, Paul. 2012. Konseptuell fysikk. 5. Ed Pearson.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, F. (2009). University Physics Vol. 1
- Wikipedia. Gravitasjonsenergi. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Gravitasjonsenergi. Gjenopprettet fra: en.wikipedia.com



Ingen har kommentert denne artikkelen ennå.