De potensiell energi Det er energien kroppene har i kraft av sin konfigurasjon. Når objekter samhandler, er det krefter mellom dem som kan utføre arbeid, og denne evnen til å utføre arbeid, som er lagret i deres disposisjon, kan oversettes til energi..
For eksempel har mennesker utnyttet fossens potensielle energi siden uminnelige tider, først ved å spinne fabrikker og deretter på vannkraftverk..
På den annen side har mange materialer en bemerkelsesverdig evne til å utføre arbeid ved å deformere og deretter gå tilbake til sin opprinnelige størrelse. Og under andre omstendigheter tillater arrangementet av den elektriske ladningen lagring av elektrisk potensiell energi, som for eksempel i en kondensator.
Potensiell energi gir mange muligheter til å bli transformert til andre former for brukbar energi, derav viktigheten av å kjenne lovene som styrer den..
Artikkelindeks
Den potensielle energien til et objekt har sitt utspring i kreftene som påvirker det. Potensiell energi er imidlertid en skalar størrelse, mens kreftene er vektorer. Derfor, for å spesifisere potensiell energi, er det nok å indikere den numeriske verdien og de valgte enhetene.
En annen viktig egenskap er typen kraft som potensiell energi kan lagres med, siden ikke alle krefter har denne dyden. Bare konservative krefter lagrer potensiell energi i systemene de virker på.
En konservativ kraft er en som arbeidet ikke er avhengig av banen som følges av objektet, men bare av startpunktet og ankomstpunktet. Kraften som driver det fallende vannet er tyngdekraften, som er en konservativ kraft.
På den annen side har elastiske og elektrostatiske krefter også denne kvaliteten, derfor er det potensiell energi forbundet med dem..
Styrker som ikke oppfyller ovennevnte krav kalles ikke-konservative; eksempel på dem er i friksjon og luftmotstand.
Siden potensiell energi alltid kommer fra konservative krefter som de som allerede er nevnt, snakker vi om gravitasjonspotensiell energi, elastisk potensiell energi, elektrostatisk potensiell energi, kjernepotensial energi og kjemisk potensiell energi..
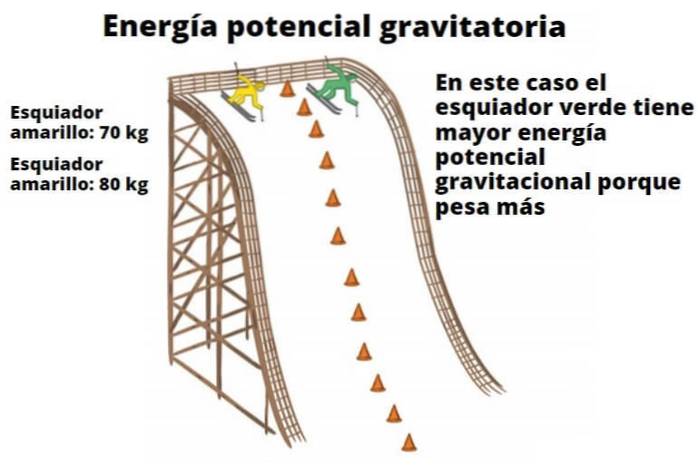
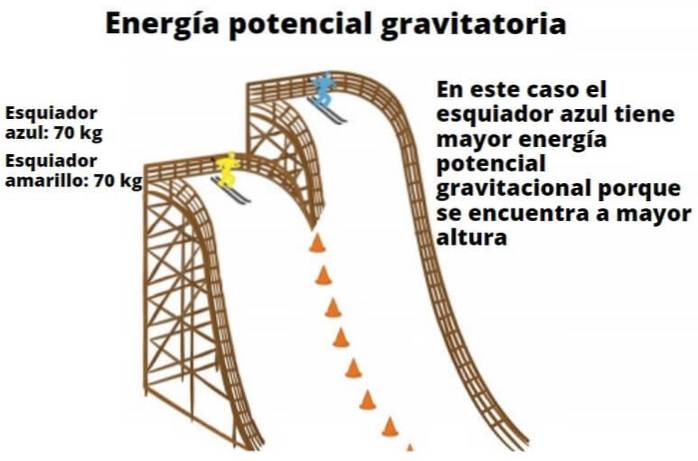
Ethvert objekt har potensiell energi som en funksjon av høyden fra bakken. Dette tilsynelatende enkle faktum illustrerer hvorfor fallende vann er i stand til å drive turbiner og til slutt forvandles til elektrisk energi. Skiløpereksemplet vist her viser også forholdet mellom vekt og høyde til gravitasjonspotensialenergi.
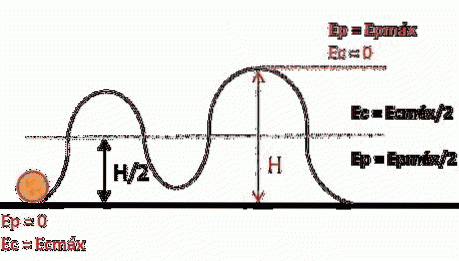
Et annet eksempel er en berg- og dalbane bil, som har høyere potensiell energi når den er i en viss høyde over bakken. Når den har nådd bakkenivå, er høyden lik null, og all dens potensielle energi har blitt transformert til kinetisk energi (bevegelsesenergi).
Gjenstander som fjærer, buer, armbrøst og gummibånd er i stand til å lagre elastisk potensiell energi..
Elastisiteten til et legeme eller et materiale er beskrevet av Hookes lov (opp til visse grenser), som forteller oss at styrken som er i stand til å utøve når den er komprimert eller strukket er proporsjonal med dens deformasjon.
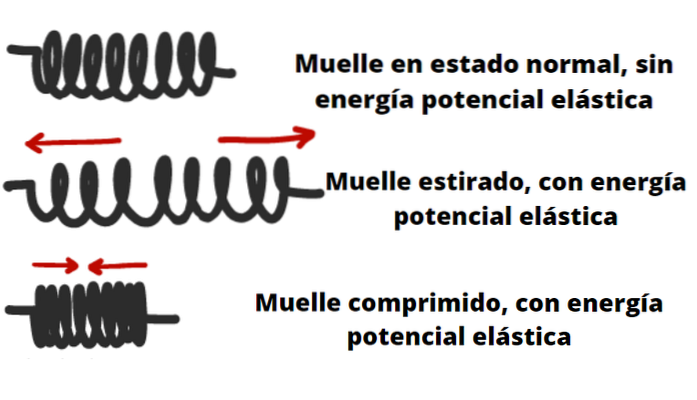
For eksempel i tilfelle en fjær eller vår, betyr dette at jo mer den krymper eller strekker seg, jo større kraft kan den utøve på en gjenstand plassert i den ene enden..
Det er energien som elektriske ladninger har i kraft av sin konfigurasjon. Elektriske ladninger med samme tegn frastøter hverandre, så for å plassere et par positive - eller negative - ladninger i en bestemt posisjon, må en ekstern agent utføre arbeid. Ellers hadde de en tendens til å skille seg.
Dette arbeidet lagres slik lastene ble lokalisert. Jo nærmere ladningene til det samme tegnet er, jo høyere potensiell energi vil konfigurasjonen ha. Det motsatte skjer når det kommer til masse forskjellige tegn; hvordan de tiltrekker seg, jo nærmere de er, jo mindre potensiell energi har de.
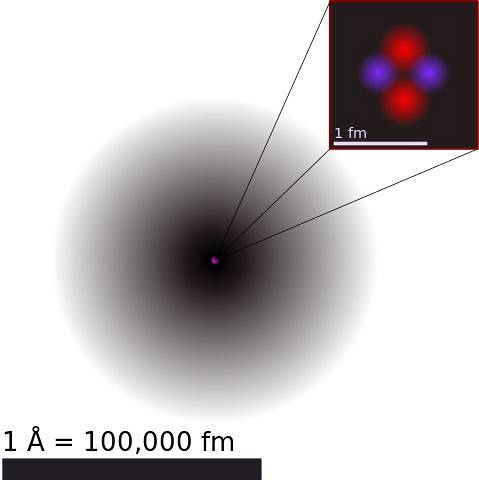
Atomkjernen består av protoner og nøytroner, generisk kalt nukleoner. Førstnevnte har en positiv elektrisk ladning og sistnevnte er nøytrale..
Siden de er agglomererte i et lite rom utenom fantasien, og å vite at ladninger av samme tegn frastøter hverandre, lurer man på hvordan atomkjernen forblir sammenhengende.
Svaret ligger i andre krefter enn elektrostatisk frastøting, typisk for kjernen, for eksempel den sterke kjernefysiske interaksjonen og den svake kjernefysiske interaksjonen. Dette er veldig sterke krefter, som langt overstiger den elektrostatiske kraften.
Denne formen for potensiell energi kommer fra hvordan atomer og molekyler av stoffer er ordnet, i henhold til de forskjellige typer kjemiske bindinger..
Når en kjemisk reaksjon oppstår, kan denne energien transformeres til andre typer, for eksempel ved hjelp av et batteri eller elektrisk batteri.
Potensiell energi er til stede i det daglige på mange måter. Å observere effekten er like enkelt som å plassere ethvert objekt i en viss høyde og være sikker på at det kan rulle eller falle når som helst.
Her er noen manifestasjoner av de typer potensiell energi som tidligere er beskrevet:
-Berg og dalbaner
-Biler eller baller som ruller nedoverbakke
-Buer og piler
-Elektriske batterier
-En klokkependel
-Sving på en sving
-Hopp på en trampoline
-Bruk en uttrekkbar penn.
Se: potensielle energieksempler.
Den potensielle energien avhenger av arbeidet som utføres av kraften, og dette avhenger i sin tur ikke av banen, så det kan sies at:
-Hvis A og B er to punkter, er arbeidet WAB nødvendig å gå fra A til B er lik arbeidet som er nødvendig for å gå fra B til A. Derfor: WAB = WBA, så:
WAB + WBA = 0
-Og hvis to forskjellige baner 1 og 2 blir forsøkt å slutte seg til punkt A og B, er arbeidet som er utført i begge tilfeller også det samme:
W1 = Wto.
I begge tilfeller opplever objektet en endring i potensiell energi:
Endring = Endelig potensiell energi - Innledende potensiell energi
ΔU = Uendelig - ELLERførste = UB - ELLERTIL
Den potensielle energien til objektet er definert som det negative av arbeidet utført av den (konservative) kraften:
ΔU = -WAB
Men siden arbeid er definert av denne integralen:
Merk at enhetene med potensiell energi er de samme som arbeidene. I SI International System er enheten joule, som forkortes J og tilsvarer 1 newton x meter, av engelsk fysiker James Joule (1818-1889).
Andre enheter for energi inkluderer cgs erg, pund-kraft x fot, BTU (British Thermal Unit), kalorier og kilowatt-timer.
La oss se noen spesielle tilfeller av hvordan man beregner potensiell energi.
I nærheten av jordoverflaten peker tyngdekraften loddrett nedover og størrelsen er gitt av ligningen Vekt = masse x tyngdekraft.
Betegner den vertikale aksen med bokstaven "y" og tildeler denne retningen enhetsvektoren j, positiv opp og negativ ned, endringen i potensiell energi når en kropp beveger seg fra y = yTIL før y = yB Det er:
U (y) = mgy
Hookes lov forteller oss at kraften er proporsjonal med deformasjonen:
F = -k.x
Her x er deformasjonen og k er en egenkonstant av våren, som indikerer hvor stiv den er. Gjennom dette uttrykket beregnes den elastiske potensielle energien, med tanke på det Jeg er enhetsvektoren i horisontal retning:
U (x) = ½ kxto
Når du har et punkt elektrisk ladning Q, produserer det et elektrisk felt som oppfatter en annen punktladning hva, og at den fungerer på den når den flyttes fra en posisjon til en annen midt på feltet. Den elektrostatiske kraften mellom topunktsladninger har en radiell retning, symbolisert av enhetsvektoren r:
En vår hvis konstant er k = 10,0 N / cm strekker seg opprinnelig 1,00 cm fra likevektlengden. Du blir bedt om å beregne den ekstra energien som kreves for å strekke fjæren opp til 5,00 cm utover dens likevektlengde..
Ved å erstatte x = 1,00 cm direkte i ligningen for U (x) får vi N.cm, men centimeterene må konverteres til meter for å få energien i joule:
U (1) = 0,5 x 10,0 N / cm x (1,00 cm)to = 5 N. cm = 0,05 J; U (5) = 0,5 x 10,0 N / cm x (5,00 cm)to = 125 N.cm = 1,25 J
Derfor er den etterspurte energidifferansen 1,25 - 0,05 J = 1,20 J.
En liten blokk frigjøres fra hvile fra punkt A, for å gli langs den friksjonsløse buede rampen til punkt B. Derfra går den inn i en lang, grov horisontal overflate, med en dynamisk friksjonskoeffisient μk = 0,2. Finn hvor langt fra punkt B det stopper, forutsatt at hTIL= 3m.
Når blokken er i en høyde hTIL Med hensyn til bakken har den gravitasjonspotensial energi på grunn av høyden. Når den frigjøres, konverteres denne potensielle energien gradvis til kinetisk energi, og når den glir nedover den glatte buede rampen, øker hastigheten..
Under banen fra A til B kan ikke ligningene med jevnt variert rettlinjet bevegelse brukes. Selv om tyngdekraften er ansvarlig for bevegelsen av blokken, er bevegelsen den opplever mer kompleks, fordi banen ikke er rettlinjet.
Siden tyngdekraften er en konservativ kraft og det ikke er noen friksjon på rampen, kan du bruke bevaring av mekanisk energi for å finne hastigheten på slutten av rampen:
Mekanisk energi i A = Mekanisk energi i B
m.g.hTIL + ½ m.vTILto = m.g.hB + ½ m.vBto
Uttrykket forenkles ved å merke seg at massen vises i hvert begrep. Det frigjøres fra hvile vTIL = 0. Og hB er på bakkenivå, hB = 0. Med disse forenklingene reduseres uttrykket til:
vBto = ghTIL
Nå begynner blokken sin ferd i den grove delen med denne hastigheten og stopper til slutt ved punkt C. Derfor vC = 0. Mekanisk energi er ikke lenger bevart, fordi friksjon er en avledende kraft, som har utført arbeid på blokken gitt av:
Wta på = - friksjonskraft x tilbakelagt avstand
Dette arbeidet har et negativt tegn, siden den kinetiske friksjonen bremser objektet og motarbeider dets bevegelse. Størrelsen på den kinetiske friksjonen Fk Det er:
Fk = μk .N
Hvor N er størrelsen på den normale kraften. Den normale kraften utøves av overflaten på blokken, og siden overflaten er helt horisontal, balanserer den vekten P = mg, derfor er størrelsen på det normale:
N = mg
Som leder til:
Fk = μk .mg
Arbeidet som Fk gjør om blokken er: Wk = - fk .D = - μk .mg.D.
Dette arbeidet tilsvarer endring i mekanisk energi, beregnet slik:
Mekanisk energi i C - Mekanisk energi i B =
ΔEm = (UC +KC) - (ELLERB + KB) = - μk .mg.D
I denne ligningen er det noen begreper som forsvinner: KC = 0, siden blokken stopper ved C og U også forsvinnerC = UB, fordi disse punktene er på bakkenivå. Forenklingen resulterer i:
- KB = - μk .m.g.D
½ m.vBto = μk .m.g.D
Massen avbrytes igjen og D kan oppnås som følger:
D = (½ vBto) / (μk . g) = (½ vBto) / (μk . g) = (½g.hTIL) / (μk . g) = (½tTIL) / μk = 0,5 x 3 m / 0,2 = 7,5 m
Ingen har kommentert denne artikkelen ennå.