
Translasjonsbalanseforhold, eksempler, øvelser
En gjenstand påstås å være i translasjonell likevekt når summen av kreftene som virker på den er null. Dette betyr ikke at det nødvendigvis er hvile, men bevegelsen, hvis den eksisterer, ville være ensartet rettlinjet eller utelukkende roterende, når det gjelder et stort objekt..
Forholdene for mekanisk likevekt er basert på Newtons mekaniske lover. Den første loven forteller oss at et objekt er i ro eller beveger seg med jevn rettlinjet MRU, forutsatt at ingen nettokraft virker på det.

Nå er nettokraften eller den resulterende kraften bare vektorsummen av alle kreftene som virker på objektet. I følge Newtons andre lov må denne summen være lik produktet mellom massen og akselerasjonen, men hvis objektet ikke akselereres, forsvinner denne summen.
Og i fravær av akselerasjon, er det de to nevnte mulighetene: kroppen er i ro, det vil si at den ikke beveger seg, eller hvis den gjør det, må den være med MRU. I det første tilfellet snakker vi om statisk transnasjonal likevekt, og i det andre dynamisk.
Translasjonsvekt er en viktig faktor i mange aspekter av engineering, for eksempel i konstruksjon. Elementene som utgjør en bygning: bjelker, kabler, rammer og mer, må være i balanse for å garantere stabiliteten til kabinettet.
Oversettelsesbalanse søkes også i mobile strukturer, som rulletrapper, transportbånd og i utøvelsen av mange idretter..
Artikkelindeks
- 1 Tilstand for translasjonsvekt
- 1.1 Diagrammer over fritt kropp
- 2 Eksempler på translasjonell likevekt
- 2.1 Bygninger og veier
- 2.2 Bøker og gjenstander i hyllene
- 2.3 Møblene
- 2.4 Trafikklys
- 2.5 Offentlig belysning
- 3 Øvelsen løst
- 3.1 Løsning
- 4 Referanser
Translasjonell likevektstilstand
Anta at flere krefter virker på en kropp, som vi betegner som F1, Fto, F3... . Fn, ved hjelp av fet skrift for å markere det faktum at krefter er vektorer og må legges til som sådan.
Vektorsummen av alle disse kreftene kalles resulterende kraft eller nettokraft. Hvis denne summeringen resulterer i nullvektoren, er vilkåret for den translasjonelle likevekten oppfylt:
F1+ Fto+ F3... .+ Fn = 0
Denne tilstanden kan skrives kompakt ved hjelp av summeringsnotasjon:
∑ FJeg = 0
Når det gjelder komponentene i den resulterende kraften, kan ovenstående ligning, som er vektor, brytes ned i tre skalarligninger, en for hver komponent av den resulterende kraften:
∑ Fix = 0; ∑ FY = 0 og ∑ Fz = 0
I praksis er det ikke lett å avbryte summen av krefter, fordi friksjon er en kontaktkraft mellom overflater som neppe blir fullstendig kansellert av noen annen kraft..
Dette er grunnen til at virkelige objekter nesten aldri er unntatt fra ytre krefter, og som en konsekvens er det vanskelig å oppnå translasjonell likevekt.
Så ingeniører bruker mekanismer for å redusere friksjon, for eksempel lagre og bruk av smøreoljer..
Gratis kroppsdiagrammer
Frikroppsdiagrammet er et diagram der kreftene som virker på kroppen blir tegnet. Når du søker translasjonell likevekt, må disse kreftene balanseres. For eksempel, hvis en vertikal kraft rettet nedover virker, slik som vekt, så må det være en vertikal kraft oppover som har nøyaktig samme størrelse.
Denne kraften kan leveres av hånden som støtter gjenstanden slik at den ikke faller, et tau eller bare overflaten på et bord.
Hvis det er en kraft tangentiell til overflaten, for eksempel kinetisk eller statisk friksjon, må det være en annen motstridende kraft for at balanse skal eksistere. La oss for eksempel se på vekten som henger fra strengene vist i følgende figur.
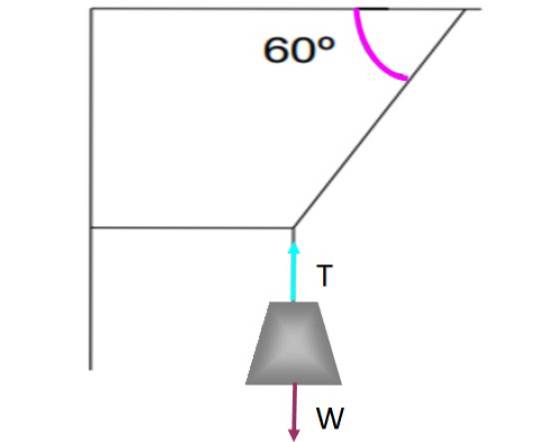
Vekten holdes i translasjonsbalanse og uten å bevege seg, takket være det vertikale tauet som holder den ved å utøve en spenning T som kompenserer for vekten W. Hver kraft er representert på vekten av en pil, hver av samme størrelse og med samme retning, men motsatt retning..
Balanseringskraften
Anta at et sett med krefter virker på et objekt. Dette kalles a styrkesystem hvorfra den resulterende kan bli funnet som forklart ovenfor: ved å vektlegge hver av kreftene i systemet.
Vel, den motsatte styrken til denne resulterende kalles balanseringskraft. Hvis den resulterende kraften er FR og balanseringskraften er OG, deretter:
OG + FR = 0
Derfor:
OG = - FR
Eksempler på translasjonell likevekt
Mange gjenstander som vi finner på daglig basis, i og utenfor hjemmet, er i translasjonell likevekt:
Bygninger og veier
Bygninger og veier er bygget for å forbli stabile og ikke velte eller kollapse. Imidlertid, i skyskrapere og generelt veldig høye bygninger, er det nødvendig med en viss fleksibilitet for å motstå vindens handling..
Bøker og gjenstander i hyllene
Bøker i et bibliotek og produkter i butikkhyllene er gjenstander som forblir i translasjonell likevekt og ikke beveger seg..
Møblene
Møblene, flatskjerm-TV og bildene på veggen, samt lampene som henger fra taket, for å nevne noen få gjenstander, er i translasjonsbalanse..
Trafikklys
Trafikklysene er festet med stolper og kabler, slik at de ikke faller. Likevel vet vi at vinden får dem til å svinge.
Offentlig belysning
Gatelysene er også i translasjonsbalanse, festet på lyktestolpene, som gatelyset i hovedbildet..
Treningen løst
Hvor stor må styrken Fs av statisk friksjon slik at boksen i figuren forblir i ro midt i det skråplanet i en vinkel α på 37º? Boksenes masse er m = 8 kg.
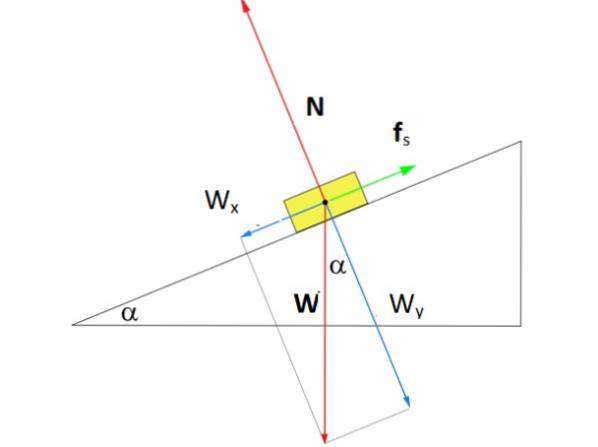
Løsning
Figuren viser frikroppsdiagrammet til boksen på flyet. Det er tre krefter som virker på det: vekt W, rettet vertikalt nedover, det normale N, som er den vinkelrette kraften som utøves av overflaten av planet på boksen, og til slutt den statiske friksjonskraften Fs som er i motsetning til at boksen glir nedoverbakke.
Den translasjonelle likevektstilstanden sier at:
W + N + Fs = 0
Men vi må huske at dette er en vektorsum og for å utføre det er det nødvendig å spalte kreftene i komponenter langs koordinataksene..
På figuren er det tegnet et koordinatsystem der x-aksen går parallelt med overflaten til det skråplanet. Med dette valget faller den statiske friksjonen på aksen, mens normal er på y-aksen. Vekt er den eneste kraften som er tilbøyelig og må brytes ned ved hjelp av trigonometri:
Wx = W. sin α
WY = W. cos α
Summen av krefter langs hver akse er:
∑ FY = N - WY = 0
∑ Fx = fs - Wx = 0
Fra denne siste ligningen følger det at:
Fs = Wx
Og som Wx = W. sin α og størrelsen på vekten i sin tur er W = m.g, hvor g er tyngdekraftsverdien, så er størrelsen på den statiske friksjonen ganske enkelt:
Fs = m⋅g⋅sen α = 8 kg × 9,8 m / sto × sin 37º = 47,2 N.
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 2. Dynamikk. Redigert av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysikk. 2. plass. Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7ma. Ed. Cengage Learning.
- Tippens, P. 2011. Fysikk: Konsepter og applikasjoner. 7. utgave. Mcgraw hill.



Ingen har kommentert denne artikkelen ennå.