Tilfeldig feilformel og ligninger, beregning, eksempler, øvelser

De tilfeldig feil av en fysisk størrelse består av de uforutsigbare variasjonene av målene for den størrelsen. Disse variasjonene kan produseres av fenomenet som måles, av måleinstrumentet eller av observatøren selv..

En slik feil er ikke fordi noe har blitt gjort galt under eksperimentet, men er en feil som ligger i måleprosessen eller fenomenet som studeres. Dette fører til at den målte mengden noen ganger er litt høyere og noen ganger litt mindre, men den svinger vanligvis rundt en sentral verdi..

I motsetning til tilfeldig feil kan systematisk feil være forårsaket av en dårlig kalibrering eller en utilstrekkelig skaleringsfaktor i måleinstrumentet, til og med en feil i eksperimentelt utstyr, eller en utilstrekkelig observasjon, som forårsaker et avvik i samme retning..

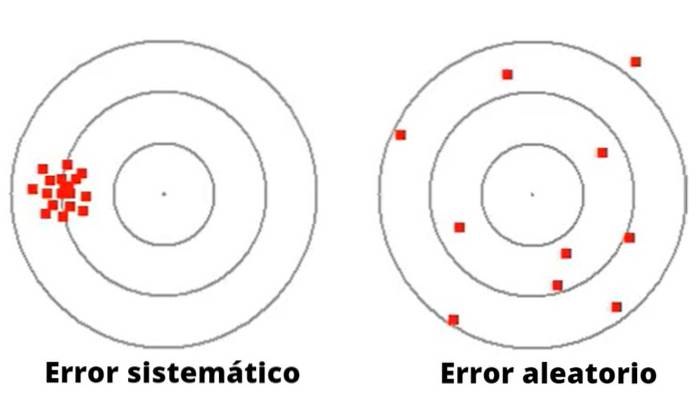
Figur 1 illustrerer forskjellen mellom systematisk og tilfeldig feil i spillet med å kaste pil på et mål med sirkler..

For venstre er pilene konsentrert rundt et punkt langt fra sentrum. Lanseringen av disse pilene har, selv om det er et godt mål, en systematisk feil, kanskje av visuell opprinnelse, eller i veien for å kaste.

På den annen side har bæreraketten til høyre (i figur 1) en stor spredning rundt det sentrale målet, derfor er det en veldig upresis bærerakett, med dårlig mål, som ufrivillig begår en tilfeldig feil..

Artikkelindeks

• 1 Formler og ligninger i tilfeldig feil
  • 1.1 Gjennomsnittsverdi og standardavvik
• 2 Hvordan beregne den tilfeldige feilen?
• 3 Eksempler på tilfeldige feil
  • 3.1 Måling av lengde med målebånd eller linjal
  • 3.2 Vindens hastighet
  • 3.3 Når du leser volumet på en gradert sylinder
  • 3.4 Når du måler barnets høyde
  • 3.5 Når du bruker baderomsvekten
• 4 Øvelse løst
  • 4.1 Løsning
• 5 Referanser

Formler og ligninger i tilfeldig feil

Når tilfeldig feil blir observert i måleprosessen, er det nødvendig å gjenta målingen flere ganger, siden fra statistisk synspunkt, jo større antall målinger, jo mindre er feilen i det endelige måleestimatet..

I hver måling er det selvfølgelig nødvendig å passe på at forholdene de utføres under alltid er de samme.

Anta at målingen gjentas n ganger. Siden det er tilfeldig feil i hver måling, vil den ha en litt annen verdi. Anta at settet med n målene er:

x₁, x_to, x₃,..., x_n

Så hvilken verdi å rapportere for tiltaket? 

Gjennomsnittlig verdi og standardavvik

De middelverdi eller gjennomsnitt av settet med tiltak, som vi betegner med og beregnes som følger:

= (x₁ + x_to + x₃ +… + X_n) / n

Standardavvik

Dette resultatet har imidlertid en feilmargin gitt av standardavviket. For å definere det, må du først vite avviket og deretter avviket:

-Avvik d_Jeg  hva hver målte verdi har xi med hensyn til gjennomsnittsverdien Det er:

d_Jeg = x_Jeg -

Hvis gjennomsnittet av avvikene ble beregnet, ville det systematisk oppnås = 0, som: 

= (d₁ + d_to + d₃ +… + D_n) / n =

= [(x₁ - ) + (x_to - ) +… + (X_n - )] / n

= (x₁+ x_to +… + X_n) / n - n / n = - = 0

-Gjennomsnittet av avvikene er ikke nyttig for å vite spredningen av tiltakene. På den annen side er gjennomsnittsverdien av kvadratet til avvikene eller avviket, betegnet med σ^to, hvis det er.

Den beregnes i henhold til følgende formel:

σ^to = (d₁^to + d_to^to +…. + D_n^to ) / (n -1)

I statistikken kalles denne mengden forskjell.  

Og kvadratroten til variansen er kjent som standardavvik σ:

σ = √ [(d₁^to + d_to^to +…. + D_n^to ) / (n -1)] 

Standardavviket σ forteller oss at:

1.- 68% av målingene som er gjort faller innenfor intervallet [ - σ , + σ]. 

2.- 95% av målingene er i intervallet [ - 2σ , + 2σ].

3.- 99,7% av målingene som er tatt er i området [ - 3σ , + 3σ].

Hvordan beregne den tilfeldige feilen?

Måleresultatet er middelverdi av n målinger betegnet med og beregnes i henhold til følgende formel:

= (∑x_Jeg) / n

derimot Det er ikke den "eksakte" verdien av målingen, siden påvirkes av tilfeldig feil ε, som beregnes slik:

ε = σ / √n

Hvor:

σ = √ [(∑ (xi - )^to ) / (n -1)]

Det endelige resultatet av målingen må rapporteres på en av følgende måter:

1. ± σ / √n = ± ε med et konfidensnivå på 68%.
2. ± 2σ / √n = ± 2ε med et konfidensnivå på 95%.
3. ± 3σ / √n = ± 3ε med et konfidensnivå på 99,7%.

Den tilfeldige feilen påvirker den siste signifikante figuren av målingen, som vanligvis sammenfaller med måling av instrumentet. Men hvis den tilfeldige feilen er veldig stor, kan de to siste signifikante sifrene bli påvirket av variasjon..

Eksempler på tilfeldige feil

Tilfeldige feil kan vises i forskjellige tilfeller der en måling utføres:

Måle en lengde med et målebånd eller linjal

Når en lengde måles med en linjal eller målebånd og målingene faller mellom merkene på skalaen, estimeres den mellomliggende verdien.

Noen ganger har estimatet et overskudd og andre ganger en mangel, slik at tilfeldig feil blir introdusert i måleprosessen.

Vindens hastighet

Ved måling av vindhastighet kan det være endringer i avlesningen fra et øyeblikk til et annet på grunn av fenomenets skiftende natur..

Når du leser volumet på en gradert sylinder

Når volumet leses med en gradert sylinder, og til og med prøver å minimere parallaksfeilen, endres observasjonsvinkelen til menisken litt hver gang den måles, og det er derfor målingene påvirkes av tilfeldig feil.

Når du måler barnets høyde

Når du måler høyden på et barn, spesielt hvis det er litt urolig, gjør små endringer i holdning litt avlesningen.

Når du bruker baderomsvekten

Når vi vil måle vekten vår med en badevekt, kan en liten endring i støttepunktet, til og med en endring i holdning tilfeldig påvirke målingen..

Treningen løst

En leketøyvogn kan rulle nedover et rett og skrått spor, og tiden det tar å reise hele banen måles med en stoppeklokke. 

Målingen utføres 11 ganger, og pass på å alltid slippe vognen fra samme sted uten å gi den noen impuls og holde hellingen fast..

Resultatsettet er:

3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s, 3.03s

Hva er den tilfeldige feilen til målingene?

Løsning

Som du ser er resultatene ikke unike og varierer litt..

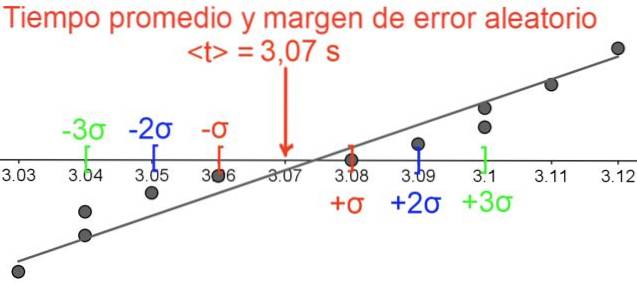
Det første er å beregne gjennomsnittsverdien for nedstigningstiden, og oppnå 3.074545455 sekunder.

Det er ikke fornuftig å beholde så mange desimaler, siden hver måling har tre signifikante figurer og den andre desimalen for hver måling er usikker, siden den er i grenseverdien for stoppeklokken, og resultatet blir derfor avrundet til to desimaler:

= 3,08 s.

Med kalkulatoren i statistisk modus er standardavviket σ = 0,03 s og standardfeilen er σ / √11 = 0,01 s. Det endelige resultatet uttrykkes slik:

Nedstigningstid 

3,08 s ± 0,01 s (med et konfidensnivå på 68%)

3,08 s ± 0,02 s (med 95% konfidensnivå)

3,08 s ± 0,03 s (med et konfidensnivå på 99,7%)

Referanser

1. Canavos, G. 1988. Sannsynlighet og statistikk: Applikasjoner og metoder. Mcgraw hill.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørvitenskap og vitenskap. 8. plass. Utgave. Cengage.
3. Helmenstine A. Tilfeldig feil vs. systematisk feil. Gjenopprettet fra: thoughtco.com
4. Laredo, E. Feil i media. Gjenopprettet fra: usb.ve.
5. Levin, R. 1988. Statistikk for administratorer. 2. plass. Utgave. Prentice hall.