
Strekkspenningsformel og ligninger, beregning, øvelser
De Stressbelastning Det er definert som kraften vinkelrett på arealet per arealeenhet som påføres et objekt i endene for å utøve trekkraft på det, takket være hvilket det forlenges. Dimensjonene er kraft / område, og i matematisk form kan vi uttrykke det slik:
τ = F / A
Enhetsenheten i det internasjonale systemet for enheter er den samme som den som brukes for trykk: pascal, forkortet Pa, som tilsvarer 1 newton / mto.

I strekkinnsatsen er det to krefter som påføres i samme retning og motsatte retninger, som strekker kroppen. Hvis opprinnelig lengden på objektet var Leller, ved påføring av strekkspenning er den nye lengden L og strekningen ΔL beregnes av:
ΔL = L - Leller
Faste objekter har elastisitet i større eller mindre grad, noe som betyr at når strekkbelastningen forsvinner, går de tilbake til sine opprinnelige dimensjoner..
Dette skjer så lenge spenningen ikke er så stor at den forårsaker permanent deformasjon. Gummi, gummi eller gummimaterialer er gode for å lage elastiske gjenstander og blant annet hår og hud har denne kvaliteten..
Artikkelindeks
- 1 Sil
- 2 Hvordan beregnes strekkbelastning? (Eksempler)
- 2.1 Beregningseksempel
- 3 Løst øvelser
- 4 - Øvelse 1
- 5 - Øvelse 2
- 6 Referanser
Enhetsdeformasjon
Når man studerer hvordan legemer deformeres under stress, er det veldig praktisk å definere begrepet press, en dimensjonsløs mengde. Stamme er betegnet med den greske bokstaven δ (små bokstaver "delta") og beregnes som følger:
δ = AL / Leller
Stamme brukes til å sammenligne evaluering av deformasjonen av gjenstanden under stress. La oss se det slik: å strekke en 1 meter lang stang 1 cm er ikke det samme som å strekke en 10 m lang stang 1 cm. I det første tilfellet er deformasjonen mye mer signifikant enn i det andre.
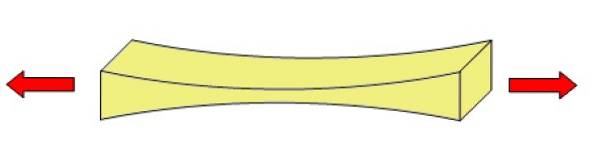
Hvordan beregnes strekkbelastning? (Eksempler)
Den engelske fysikeren og samtiden til Newton ved navn Robert Hooke (1635-1703), undersøkte kroppens elastiske egenskaper og etablerte loven som bærer hans navn. Med det er den påførte spenningen relatert til deformasjonen som oppleves når spenningen er liten:
Stress ∝ Stamme (enhet)
Det er logisk å forvente at jo høyere strekkbelastning, jo større forlengelse vil oppstå. Bruk av definisjonene gitt ovenfor:
τ ∝ δ
Konstanten av proporsjonalitet som er nødvendig for å etablere likhet, betegnes Y og er kjent som Youngs modul eller elastisitetsmodul, karakteristisk for materialer:
τ = Y⋅δ
Youngs modul har de samme strekkbelastningsenhetene, siden belastningen er dimensjonsløs.
Så, en måte å beregne strekkbelastningen i et legeme med elastiske egenskaper på er å måle belastningen og kjenne Youngs modul. Denne mengden er bestemt eksperimentelt for mange materialer og er tabellert.
Beregningseksempel
Anta at en ledning laget av herdet stål med en diameter på 3 mm utsettes for en strekkspenning, som henger fra den med en vekt på 250 N, hva ville være størrelsen på nevnte spenning?
Vel, vi kan bruke definisjonen av strekkbelastning som forholdet mellom kraften vinkelrett på overflaten og arealet på den overflaten. La oss først beregne området, forutsatt at en ledning med sirkulært tverrsnitt:
A = π. (d / 2)to = π. (dto / 4)
Ledningens diameter er 3 mm, og disse enhetene må forvandles til meter:
d = 3 x 10-3 m.
A = π. (3 x 10-3 m)to / 4 = 7,07 x 10-6 mto.
Strekkbelastningen produseres av vekten som henger fra ledningen, som påføres vinkelrett på tverrsnittet, og derfor:
τ = 250 N / 7,07 x 10-6 mto = 3,5 x 10 7 Pa
Pascal er en ganske liten enhet, så multipler er ikke uvanlige. Å vite at 1 mega-pascal (MPa) er 106 pascal forblir strekkbelastningen:
τ = 35 MPa
Løst øvelser
- Øvelse 1
Elastisitetsmodulen til en stang er 4 x 10elleve Pa. Hvilken belastning oppnås ved å påføre en strekkspenning på 420 MPa?
Løsning
Ligningen du skal bruke er:
τ = Y⋅δ
Med den beregner vi belastningen:
δ = τ / Y = 420 x 106 Pa / 4 x 10elleve Pa = 0,00105
δ = AL / Leller
Derfor er stammen ΔL:
AL = 0,00105 Leller
Hvis for eksempel stangen opprinnelig var 1 meter lang, med den strekkbelastningen, strekker den seg bare 0,00105 m = 1,05 mm.
- Øvelse 2
En ståltråd er 1,50 m lang og har en diameter på 0,400 mm. Den ene enden er festet i taket og en bakkenreflektor er festet til den andre. m = 1,50 kg, som frigjøres. Regne ut:
a) Strekkingen av ledningen.
b) Sil og prosent belastning. Er det mulig at ledningen går i stykker under reflektorens vekt??
Løsning
Ledningen kommer til å strekke seg, siden den reflekteres når den henges, blir den utsatt for strekk. Kraften som produserer denne innsatsen er reflektorens vekt.
Vekten til et objekt med masse m er masseproduktet ganger verdien av akselerasjonen på grunn av tyngdekraften, og derfor:
F = 1,50 kg x 9,8 m / sto = 14,7 N
Ledningens tverrsnittsareal er nødvendig:
A = π. (dto / 4) = π x (0,4 x 10-3 m) 2/4 = 1,26 x 10-7 mto.
Med disse resultatene beregnes innsatsen som utøves av ledningen:
τ = 14,7 N / 1,26 x 10-7 mto = 1,17 x 108 Pa
Ledningen har en elastisk oppførsel, derfor er det gyldig å anta at Hookes lov er oppfylt:
τ = Y⋅δ
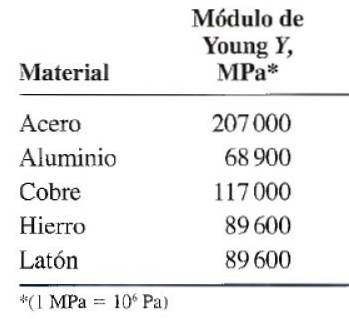
Fra tabellen med elastisitetsmodul finner vi at for stål Y = 207 x 109 Pa. I tillegg er belastningen:
δ = ΔL / Leller
Bytte i ligningen for innsatsen:
τ = Y⋅δ = Y⋅ (AL / Leller)
Derfor er strekningen:
AL = L.eller τ / Y =
= 1,50 m x 1,17 x 108 Pa / 207 x 109 Pa = 8,5 x 10-4 m = 0,849 mm.
Ledningens belastning er:
δ = AL / Leller = 8,5 x 10-4 m / 1,5 m = 5,652 x 10-4
Hvis vi uttrykker det som en prosentandel, er den prosentvise enhetsdeformasjonen 0,0565%, mindre enn 0,1%, og det forventes derfor at ledningen vil motstå reflektorens vekt uten å bryte, siden deformasjonen den opplever ikke er for stor i sammenligning til original lengde.
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Beer, F. 2010. Mekanikk av materialer. McGraw Hill. 5. Utgave.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.
- Valera Negrete, J. 2005. Notater om generell fysikk. UNAM.


Ingen har kommentert denne artikkelen ennå.