
Deler av brøker Tilfeller og eksempler
De delvise brøker er fraksjoner dannet av polynomer, der nevneren kan være et lineært eller kvadratisk polynom, og i tillegg kan det heves til en viss kraft. Noen ganger, når vi har rasjonelle funksjoner, er det veldig nyttig å omskrive denne funksjonen som en sum av delvise brøker eller enkle brøker..
Dette er fordi på denne måten kan vi manipulere disse funksjonene på en bedre måte, spesielt i tilfeller der det er nødvendig å integrere nevnte applikasjon. En rasjonell funksjon er ganske enkelt kvotienten mellom to polynomer, og de kan være riktige eller upassende.

Hvis graden av tellerens polynom er mindre enn nevneren, kalles det en rasjonell riktig funksjon; ellers er det kjent som en upassende rasjonell funksjon.
Artikkelindeks
- 1 Definisjon
- 2 saker
- 2.1 Sak 1
- 2.2 Sak 2
- 2.3 Sak 3
- 2.4 Sak 4
- 3 applikasjoner
- 3.1 Integral calculus
- 3.2 Massesaksloven
- 3.3 Differensiallikninger: logistisk ligning
- 4 Referanser
Definisjon
Når vi har en feil rasjonell funksjon, kan vi dele tellerens polynom med nevnerens polynom og dermed omskrive brøken p (x) / q (x), etter divisjonsalgoritmen som t (x) + s (x ) / q (x), hvor t (x) er et polynom og s (x) / q (x) er en riktig rasjonell funksjon.
En delvis brøkdel er en hvilken som helst riktig funksjon av polynomer, hvis nevner har formen (ax + b)n o (øksto+ bx + c)n, hvis polynomøksento + bx + c har ikke ekte røtter, og n er et naturlig tall.
For å omskrive en rasjonell funksjon i delvise brøker, er det første du må gjøre faktor nevneren q (x) som et produkt av lineære og / eller kvadratiske faktorer. Når dette er gjort, fortsetter vi med å bestemme delbrøkene, som avhenger av arten av disse faktorene..
Saker
Vi vurderer flere saker hver for seg.
Sak 1
Faktorene til q (x) er alle lineære og ingen gjentas. Nemlig:
q (x) = (a1x + b1) (tiltox + bto)… (tilsx + bs)
Der er ingen lineær faktor identisk med en annen. Når denne saken oppstår, vil vi skrive:
p (x) / q (x) = A1/(til1x + b1) + A.to/(tiltox + bto) ... + As/(tilsx + bs).
Hvor skal du1,TILto,… ,TILs er konstantene du vil finne.
Eksempel
Vi ønsker å spalte den rasjonelle funksjonen i enkle brøker:
(x - 1) / (x3+3xto+2x)
Vi fortsetter med å faktorere nevneren, det vil si:
x3 + 3xto + 2x = x (x + 1) (x + 2)
Seinere:
(x - 1) / (x3+3xto+2x) = (x - 1) / x (x + 1) (x + 2)
(x - 1) / x (x + 1) (x + 2) = A / x + B / (x + 1) + C / (x + 2)
Ved å bruke minst vanlig multiplum kan det oppnås at:
x - 1 = A (x + 1) (x + 2) + B (x + 2) x + C (x + 1) x.
Vi ønsker å oppnå verdiene til konstantene A, B og C, som kan bli funnet ved å erstatte røttene som avbryter hvert av begrepene. Ved å erstatte 0 for x har vi:
0 - 1 = A (0 + 1) (0 + 2) + B (0 + 2) 0 + C (0 + 1) 0.
- 1 = 2A
A = - 1/2.
Erstatter - 1 for x har vi:
- 1 - 1 = A (- 1 + 1) (- 1 + 2) + B (- 1 + 2) (- 1) + C (- 1 + 1) (- 1).
- 2 = - B
B = 2.
Erstatter - 2 for x har vi:
- 2 - 1 = A (- 2 + 1) (- 2 + 2) + B (- 2 + 2) (- 2) + C (- 2 + 1) (- 2).
-3 = 2C
C = -3/2.
På denne måten oppnås verdiene A = -1/2, B = 2 og C = -3/2.
Det er en annen metode for å oppnå verdiene A, B og C. Hvis på høyre side av ligningen x - 1 = A (x + 1) (x + 2) + B (x + 2) x + C (x + 1) x vi kombinerer termer, vi har:
x - 1 = (A + B + C) xto + (3A + 2B + C) x + 2A.
Siden dette er en likhet med polynomer, har vi at koeffisientene på venstre side må være lik de på høyre side. Dette resulterer i følgende ligningssystem:
A + B + C = 0
3A + 2B + C = 1
2A = - 1
Å løse dette ligningssystemet får vi resultatene A = -1/2, B = 2 og C = -3/2.
Til slutt, ved å erstatte de oppnådde verdiene har vi det:
(x - 1) / x (x + 1) (x + 2) = - 1 / (2x) + 2 / (x + 1) - 3 / (2 (x + 2)).
Sak 2
Faktorene til q (x) er alle lineære og noen gjentas. Anta at (ax + b) er en faktor som gjentar “s” ganger; deretter tilsvarer denne faktoren summen av "s" delfraksjoner.
TILs/ (øks + b)s + TILs-1/ (øks + b)s-1 +… + A1/ (øks + b).
Hvor As,TILs-1,… , TIL1 er konstantene som skal bestemmes. Med det følgende eksemplet vil vi vise hvordan du kan bestemme disse konstantene.
Eksempel
Nedbrytes i delfraksjoner:
(x - 1) / (xto(x - 2)3)
Vi skriver den rasjonelle funksjonen som en sum av delvise brøker som følger:
(x - 1) / (xto(x - 2)3) = A / xto + B / x + C / (x - 2)3 + D / (x - 2)to + E / (x - 2).
Seinere:
x - 1 = A (x - 2)3 + B (x - 2)3x + Cxto + D (x - 2) xto + E (x - 2)toxto
Ved å erstatte 2 med x, har vi det:
7 = 4C, det vil si C = 7/4.
Ved å erstatte 0 for x har vi:
- 1 = -8A eller A = 1/8.
Ved å erstatte disse verdiene i forrige ligning og utvikle har vi det:
x - 1 = 1/8 (x3 - 6xto + 12x - 8) + Bx (x3 - 6xto + 12x - 8) + 7 / 4xto +Dx3 - 2Dxto + Tidligereto(xto - 4x + 4)
x - 1 = (B + E) x4 + (1/8 - 6B + D - 4E) x3 + (- ¾ + 12B + 7/4 - 2D + 4E) xto +(3/2 - 8B) x - 1.
Ligningskoeffisienter får vi følgende ligningssystem:
B + E = 0;
1 / 8-6B + D-4E = 1;
- 3/4 + 12B + 7/4 - 2D + 4E = 0
3/2 - 8B = 0.
Å løse systemet har vi:
B = 3/16; D = 5/4; E = - 3/16.
For dette må vi:
(x - 1) / (xto(x - 2)3) = (1/8) / xto + (3/16) / x + (7/4) / (x - 2)3 + (5/4) / (x - 2)to - (3/16) / (x - 2).
Sak 3
Faktorene til q (x) er lineære kvadratiske, uten noen gjentatte kvadratiske faktorer. For dette tilfellet er den kvadratiske faktoren (aksto + bx + c) vil tilsvare delbrøken (Ax + B) / (axto + bx + c), hvor konstantene A og B er de vi vil bestemme.
Følgende eksempel viser hvordan du skal gå frem i dette tilfellet
Eksempel
Nedbrytes i enkle brøker a (x + 1) / (x3 - 1).
Først fortsetter vi med å faktorere nevneren, som gir oss som et resultat:
(x - 1) = (x - 1) (x + x +1).
Vi kan observere det (xto + x + 1) er et irredusjerbart kvadratisk polynom; det vil si at den ikke har reelle røtter. Nedbrytningen i delfraksjoner vil være som følger:
(x + 1) / (x - 1) (xto + x +1) = A / (x - 1) + (Bx + C) / (xto + x +1)
Fra dette får vi følgende ligning:
x + 1 = (A + B) xto +(A - B + C) x + (A - C)
Ved bruk av likhet med polynomer får vi følgende system:
A + B = 0;
AB + C = 1;
AC = 1;
Fra dette systemet har vi at A = 2/3, B = - 2/3 og C = 1/3. Vi erstatter, vi har det:
(x + 1) / (x - 1) (xto + x +1) = 2/3 (x - 1) - (2x + 1) / 3 (xto + x +1).
Sak 4
Til slutt er tilfelle 4 den der faktorene til q (x) er lineære og kvadratiske, hvor noen av de lineære kvadratiske faktorene gjentas.
I dette tilfellet, hvis (axto + bx + c) er en kvadratisk faktor som gjentar “s” ganger, slik at den delfraksjonen som tilsvarer faktoren (axto + bx + c) vil være:
(TIL1x + B) / (øksto + bx + c) + ... + (As-1x + Bs-1) / (øksto + bx + c)s-1 + (TILsx + Bs) / (øksto + bx + c)s
Hvor As, TILs-1,…, A og Bs, Bs-1,..., B er konstantene som skal bestemmes.
Eksempel
Vi vil dekomponere følgende rasjonelle funksjon i delvise brøker:
(x - 2) / (x (xto - 4x + 5)to)
Som xto - 4x + 5 er en irreduserbar kvadratisk faktor, vi har at nedbrytningen i delfraksjoner er gitt av:
(x - 2) / (x (xto - 4x + 5)to) = A / x + (Bx + C) / (xto - 4x +5) + (Dx + E) / (xto - 4x + 5)to
Forenkling og utvikling, sitter vi igjen med:
x - 2 = A (xto - 4x + 5)to + (Bx + C) (xto - 4x + 5) x + (Dx + E) x
x - 2 = (A + B) x4 + (- 8A - 4B + C) x3 + (26A + 5B - 4C + D) xto + (- 40A + 5C + E) x + 25A.
Fra ovenstående har vi følgende ligningssystem:
A + B = 0;
- 8A - 4B + C = 0;
26A + 5B - 4C + D = 0;
- 40A + 5C + E = 1;
25A = 2.
Når vi løser systemet, sitter vi igjen med:
A = - 2/25, B = 2/25, C = - 8/25, D = 2/5 og E = - 3/5.
Ved å erstatte de oppnådde verdiene har vi:
(x - 2) / (x (xto - 4x + 5)to) = -2 / 25x + (2x - 8) / 25 (xto - 4x +5) + (2x - 3) / 5 (xto - 4x + 5)to
applikasjoner
Integrert kalkulator
Delfraksjoner brukes primært til studier av integral kalkulus. Deretter vil vi se noen eksempler på hvordan du utfører integraler ved hjelp av delvise brøker.
Eksempel 1
Vi ønsker å beregne integralen av:
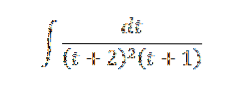
Vi kan se at nevneren q (x) = (t + 2)to(t + 1) består av lineære faktorer der en av disse gjentas; Dette er grunnen til at vi er i tilfelle 2.
Vi må:
1 / (t + 2)to(t + 1) = A / (t + 2)to +B / (t + 2) + C / (t + 1)
Vi skriver om ligningen og har:
1 = A (t + 1) + B (t + 2) (t + 1) + C (t + 2)to
Hvis t = - 1, har vi:
1 = A (0) + B (1) (0) + C (1)
1 = C
Hvis t = - 2, gir det oss:
1 = A (- 1) + B (0) (- 1) + C (0)
A = - 1
Så hvis t = 0:
1 = A (1) + B (2) (1) + C (2)
Erstatter verdiene til A og C:
1 = - 1 + 2B + 4
1 = 3 + 2B
2B = - 2
Fra ovenstående har vi at B = - 1.
Vi skriver om integralen som:
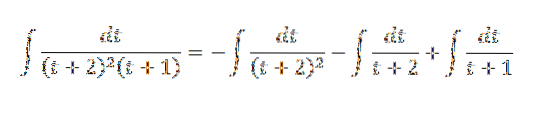
Vi fortsetter å løse det ved erstatningsmetoden:
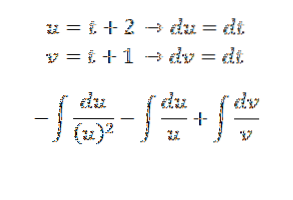
Dette er resultatet:
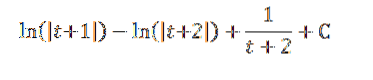
Eksempel 2
Løs følgende integral:

I dette tilfellet kan vi faktorere til q (x) = xto - 4 som q (x) = (x - 2) (x + 2). Vi er tydeligvis i tilfelle 1. Derfor:
(5x - 2) / (x - 2) (x + 2) = A / (x - 2) + B / (x + 2)
Det kan også uttrykkes som:
5x - 2 = A (x + 2) + B (x - 2)
Hvis x = - 2, har vi:
- 12 = A (0) + B (- 4)
B = 3
Og hvis x = 2:
8 = A (4) + B (0)
A = 2
Dermed sitter vi igjen med å løse den gitte integralen tilsvarer å løse:
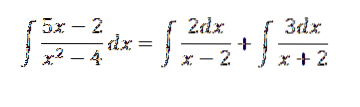
Dette gir oss som et resultat:
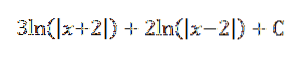
Eksempel 3
Løs integralet:
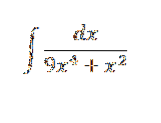
Vi har q (x) = 9x4 + xto , at vi kan faktorisere det i q (x) = xto(9xto + 1).
Denne gangen har vi en gjentatt lineær faktor og en kvadratisk faktor; det vil si at vi er i tilfelle 3.
Vi må:
1 / xto(9xto + 1) = A / xto + B / x + (Cx + D) / (9xto + 1)
1 = A (9xto + 1) + Bx (9xto + 1) + Cxto + Dxto
Gruppering og bruk av like polynomer har vi:
1 = (9B + C) x + (9A + D) x + Bx + A
A = 1;
B = 0;
9A + D = 0;
9B + C = 0
Fra dette ligningssystemet har vi:
D = - 9 og C = 0
På denne måten har vi:
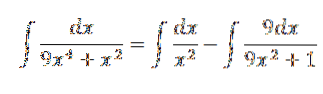
Ved å løse det ovennevnte har vi:
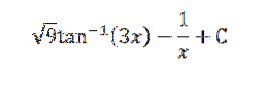
Lov om massehandling
En interessant anvendelse av de delvise fraksjonene som brukes på den integrerte kalkulen, finnes i kjemi, nærmere bestemt i loven om massehandling.
Anta at vi har to stoffer, A og B, som forener og danner et stoff C, slik at derivatet av mengden C med hensyn til tid er proporsjonalt med produktet av mengdene A og B til enhver tid.
Vi kan uttrykke loven om massehandling som følger:
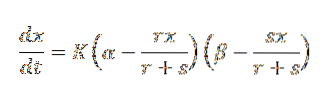
I dette uttrykket er α det opprinnelige antallet gram som tilsvarer A og β det opprinnelige antallet gram som tilsvarer B.
Videre representerer r og s antall gram henholdsvis A og B som kombineres for å danne r + s gram C. For sin del representerer x antall gram stoff C på tidspunktet t, og K er konstanten av proporsjonaliteten . Vi kan omskrive ligningen ovenfor som:

Gjør følgende endring:

Vi har at ligningen blir:

Fra dette uttrykket kan vi få:
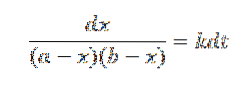
Hvor hvis a ≠ b, kan delfraksjoner brukes til integrering.
Eksempel
La oss ta for eksempel et stoff C som oppstår ved å kombinere et stoff A med et B, på en slik måte at masseloven oppfylles der verdiene til a og b er henholdsvis 8 og 6. Gi en ligning som gir oss verdien av gram C som en funksjon av tiden.
Ved å erstatte verdiene i den gitte masseloven har vi:

Når vi skiller variabler har vi:

Her kan 1 / (8 - x) (6 - x) skrives som summen av delvise brøker, som følger:
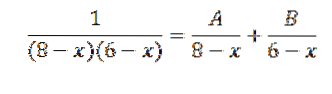
Dermed er 1 = A (6 - x) + B (8 - x)
Hvis vi erstatter 6 med x, har vi B = 1/2; og erstatter 8 med x, har vi A = - 1/2.
Integrering av delvise brøker har vi:

Dette gir oss som et resultat:

Differensiallikninger: logistisk ligning
En annen applikasjon som kan gis til delvise brøker, er i den logistiske differensiallikningen. I enkle modeller har vi at veksten i en befolkning er proporsjonal med dens størrelse; nemlig:
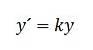
Denne saken er et ideal og anses som realistisk til det skjer at ressursene som er tilgjengelige i et system er utilstrekkelige til å støtte befolkningen..
I disse situasjonene er det mest rimelige å tenke at det er en maksimal kapasitet, som vi vil kalle L, som systemet kan opprettholde, og at vekstraten er proporsjonal med størrelsen på befolkningen multiplisert med den tilgjengelige størrelsen. Dette argumentet fører til følgende differensialligning:
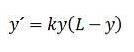
Dette uttrykket kalles logistisk differensialligning. Det er en skillbar differensialligning som kan løses med integrasjonsmetoden for delvis brøk.
Eksempel
Et eksempel kan være å vurdere en populasjon som vokser i henhold til følgende logistiske differensialligning y '= 0.0004y (1000 - y), hvis opprinnelige data er 400. Vi vil vite størrelsen på befolkningen på tidspunktet t = 2, hvor t måles i år.
Hvis vi skriver y 'med Leibnizs notasjon som en funksjon som avhenger av t, har vi:

Integralet på venstre side kan løses ved hjelp av integrasjonsmetoden for delvis brøk:
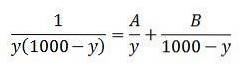
Vi kan omskrive denne siste likheten som følger:
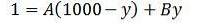
- Ved å erstatte y = 0 har vi at A er lik 1/1000.
- Ved å erstatte y = 1000 har vi at B er lik 1/1000.
Med disse verdiene er integralen som følger:
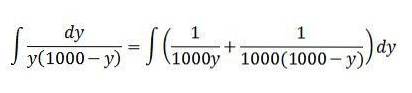
Løsningen er:

Bruke de opprinnelige dataene:

Når du rydder og vi har:

Så har vi det ved t = 2:
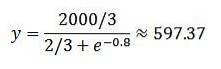
Avslutningsvis, etter to år er befolkningsstørrelsen omtrent 597,37.
Referanser
- A, R. A. (2012). Matematikk 1. Andes universitet. Publikasjonsråd.
- Cortez, I. og Sanchez, C. (s.f.). 801 Løst integraler. Nasjonalt eksperimentelt universitet i Tachira.
- Leithold, L. (1992). Beregningen med analytisk geometri. HARLA, S.A.
- Purcell, E. J., Varberg, D., og Rigdon, S. E. (2007). Beregning. Mexico: Pearson Education.
- Saenz, J. (s.f.). Integrert kalkulator. Hypotenuse.



Ingen har kommentert denne artikkelen ennå.