
Typiske brøker, eksempler, løste øvelser
De brøker eller brøktal er tallene som er representert ved å indikere kvotienten mellom to hele tall til Y b, så lenge som b er forskjellig fra 0. For eksempel er 1/3 en brøkdel som leses som "en tredjedel".
Til nummeret til det er kjent som teller av brøkdelen og til b Hva nevner Av det samme. Nevneren forteller oss hvor mange deler vi skal dele hele opp i. For sin del indikerer telleren hvor mange deler av det hele som ble tatt.

Helheten er alt du vil dele eller dele, for eksempel en pizza eller sjokoladestangen vist på figur 1. Baren er laget på en slik måte at det er veldig enkelt å dele den i 5 like deler, hvor hver del er tilsvarer 1/5 av hele linjen.
I brøkdelen eller brøknummeret 1/5 er telleren 1 og nevneren 5. Brøken leses "en femtedel".
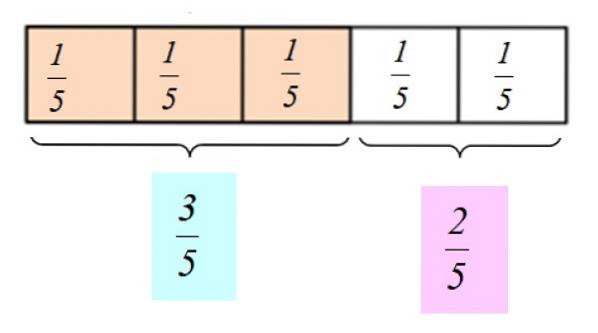
Anta at vi spiser 3 stykker sjokolade. Vi vil si at vi har spist 3/5 deler av baren, og det er 2/5 deler igjen å dele med en venn. Vi kan også si at vi spiste "tre femtedeler av sjokoladen" og ga "to femtedeler" til vennen vår.
Den grafiske representasjonen av disse brøkstallene er som følger:
Artikkelindeks
- 1 Typer brøker
- 1.1 riktige brøker
- 1.2 Feil brøker
- 1.3 Tilsynelatende brøker
- 1.4 Tilsvarende brøker
- 1.5 Irreduserbare fraksjoner
- 1.6 Blandede tall
- 2 Eksempler på brøker
- 2.1 Matkjøp
- 2.2 Matlagingsoppskrifter
- 2.3 Lengder og diametre
- 2.4 Tidsintervaller
- 3 Øvelser med brøker
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 3.3 - Øvelse 3
- 3.4 - Øvelse 4
- 4 Referanser
Typer brøker
Riktige brøker
En brøkdel er riktig når telleren er mindre enn nevneren og dermed er dens verdi mindre enn 1. Brøkene i forrige avsnitt, i eksemplet med sjokolade, er riktige brøker..
Andre eksempler på riktige brøker er: ½; 8/10; 3/4 og mer.

Feil brøker
Telleren for de upassende brøkene er større enn telleren. For eksempel 4/3, 8/5, 21/10 tilhører denne kategorien.
Tilsynelatende brøker
Disse brøkene representerer et helt tall. Blant dem er 4/2, 10/5 og 27/3, siden hvis vi ser nøye på, vil resultatet av å dele telleren med nevneren av disse brøkene gi et helt tall.
Dermed: 4/2 = 2, 10/5 = 2 og 27/3 = 9.
Tilsvarende brøker
To brøker n / m og p / q er ekvivalente når divisjon av teller etter nevner gir samme mengde. På denne måten representerer de tilsvarende brøkene den samme delen av helheten..
Som et eksempel har vi brøkene: 15/2 og 30/4. Når du deler 15 med 2, får du 7,5, men det er også det samme hvis du deler 30 med 4.
For å finne ut om to fraksjoner n / m og p / q er ekvivalente, blir følgende likhet bekreftet:
n * q = sm.p.
Uredusible brøker
Når teller og nevner deles med samme tall og forutsatt at resultatet er et helt tall, oppnås en brøk som tilsvarer originalen, men med mindre tall.
Denne prosessen fortsetter så lenge teller og nevner har nøyaktig samme deler. Når det ikke er mulig å fortsette å dele, blir irredusibel brøkdel av den opprinnelige brøkdelen.
Fordelen med å jobbe med den irredusible fraksjonen er at en ekvivalent brøk oppnås, men med mindre tall. Når du arbeider med brøker, må du sørge for å redusere dem når det er mulig for å gjøre det lettere å beregne..
Anta at brøkdelen 12/20, som teller og nevner jevn, kan begge deles med 2:
12/20 = 6/10
Og en gang til:
6/10 = 3/5
Fraksjonen 3/5 tilsvarer 12/20, men enklere.
Blandet tall
En upassende brøk tillater også representasjon som et blandet tall, såkalt fordi den har en heltall og en annen brøkdel, hvor brøkdelen er en skikkelig brøkdel..
La oss se på et raskt eksempel med brøkdelen 15/2 som vi vet er lik 7,5.
Vi kan uttrykke 15/2 som et blandet tall som dette:
15/2 = 7 + 0,5
Men 0,5 = ½. Derfor er 15/2 = 7 ½ som lyder "syv og en halv".
Eksempler på brøker
Fraksjonelle tall er nødvendige fordi både naturlige og heltall er utilstrekkelige når vi vil dele ting som godteribaren.
Og det er derfor det er et uendelig utvalg av målemønstre og objekter hvis spesifikasjoner inkluderer brøktal, for ikke å nevne antall hverdagssituasjoner der disse er nødvendige..
Mat handel
I land der det metriske systemet brukes, er det vanlig å bruke kiloen for å referere til vekten til mange matvarer. Vi ønsker ikke alltid å kjøpe hele mengder, men litt mer eller litt mindre.
Derfor spør vi:
- ½ kg fisk
- ¾ kg tomater
- ¼ kilo løk
- 1 ½ kg fersken (1 kilo og en halv).
Og når du bruker de angelsaksiske målestandardene, skjer det samme: vi trenger to og et halvt pund eller 1/4 av et pund av noe.
Alle disse tallene er brøkdeler og tilsvarer, som vi har sett, to forskjellige typer brøker: riktig og upassende..
Kjøkkenoppskrifter
Matlagingsoppskrifter bruker ofte brøktal for å indikere mengden av visse ingredienser. For eksempel:
- ½ kopp mel
- ¾ kg sukker for å tilberede en kake.
Lengder og diametre
Dimensjoner på møbler, tekstilstykker og alle slags husholdningsredskaper måles i brøkdeler av en meter eller en tomme, enten det bruker metrisk eller angelsaksisk desimalsystem..
Selv i land der det metriske systemet hersker, kommer kommersielle kobber-, stål- og andre rørleggerrør ofte med diametre spesifisert i tommer. Også annen maskinvare som skruer og muttere.
Siden en tomme tilsvarer 2,54 cm, blir disse brikkene, som har mindre diametre, vanligvis uttrykt i brøkdeler av en tomme..
Svært vanlige tiltak for husrør er:
- ½ tomme
- Tommer
- 3/8 og 5/8 tommer.
Tidsluker
Fraksjonelle tall brukes daglig til å uttrykke tidsintervaller som ¼, ½ og ¾ på en time, eller til og med litt lenger: 1 time og ¼ og så videre.

Øvelser med brøker
- Øvelse 1
I dag har Juanito tatt med seg en kake til bursdagen sin til skolen, og han vil distribuere den blant alle vennene sine, men han vil gi læreren et stykke som er tre ganger større enn det til barna.
Med tanke på at det er 24 barn + læreren, som du vil gi tilsvarende tre stykker til, i hvor mange stykker skal du kutte kaken??
Løsning
Hvis Juanito bare ville distribuere kaken blant vennene sine, ville de ha 1/24 hver.
Men siden han ønsker å gi en del til læreren og at stykket er tre ganger større, måtte han fordele kaken på 24 elever + 3 stykker til læreren. Med andre ord tilsvarer hvert barn 1/27 stykker og læreren 3/27 stykker.
I tillegg, hvis vi reduserer brøkdelen 3/27, oppnår vi at læreren tar 1/9 av kaken.
- Øvelse 2
Et selskap med en sjef og tre ansatte har € 6000 i inntekter hver måned. Hvor mye penger har hver person hvis sjefen vil beholde halvparten av det han har tjent?
Løsning
Hvis sjefen vil vinne halvparten, må han beholde 6000/2, noe som gjør € 3000. Av de øvrige 3000 euro som gjenstår er det de tre ansatte må distribuere. Dermed vil hver ansatt tjene 3000/3, noe som resulterer i € 1000.
- Øvelse 3
Finn den irredusible brøkdelen av:
a) 12/18 og b) 4/11
Løsning til
I det første tilfellet bemerker vi at både telleren og nevneren er jevn og delelig med 2. De er også delbare med 3, siden 12 og 18 er multipler av figuren..
Så vi kan forenkle brøken ved å dele både teller og nevner enten med 2 eller med 3, rekkefølgen er likegyldig.
Starter med å dele med 2:
12/18 = 6/9
Nå bemerker vi at både teller og nevner for denne ekvivalente brøkdelen er multipler av 3, så divider begge med denne figuren:
6/9 = 2/3
Og siden 2 og 3 er primtall, har de ikke lenger noen annen felles skiller bortsett fra 1. Vi har nådd den irredusible brøkdelen.
Den største felles divisor GCF for teller og nevner kunne også ha blitt beregnet. For 12 og 18:
GCF (12,18) = 6.
Og så deles teller og nevner med dette tallet, som tilsvarer å gjøre det trinnvis.
Løsning b
Her observerer vi at 11 er et primtall og dets delere er 1 og 11. For sin del innrømmer 4 4, 2 og 1 som delere. Med unntak av 1 har ikke disse tallene en felles divisor og derfor brøkdelen 4/11 er irreduserbar.
- Øvelse 4
Angi hvilken som er den største brøkdelen av hvert par:
a) ¾ og 5/4
b) 3/7 og 4/9
Løsning til
Når to positive brøker har samme nevner, jo større er den som har større teller. Derfor er 5/4 større, siden 5> 3.
Løsning b
Hvis brøkene n / m og p / q har forskjellige nevnere, og begge er positive, er sammenligningskriteriet som følger:
Hvis n.q> m. p, deretter n / m> p / q
Et annet alternativ er å finne desimaluttrykket til hver brøk og sammenligne.
I henhold til det første kriteriet: n = 3, m = 7, p = 4, q = 9. Derfor: n.q = 3 * 4 = 12 og m.p = 7 * 4 = 28.
Som 12< 28, ocurre que 3/7 < 4/9.
Eller vi uttrykker hver brøk som en desimal, og får dette:
3/7 = 0.428571428… .
4/9 = 0.444444444 ... .
Ellipsen indikerer at antall desimaler er uendelig. Men dette er nok til å verifisere at faktisk, 4/9> 3/7.
Referanser
- Baldor, A. 1986. Aritmetikk. Codex-utgaver og distribusjoner.
- Carena, M. 2019. Manual of Mathematics. National University of the Litoral.
- Figuera, J. 2000. Matematikk 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematiske siden. Hva er en brøkdel? Gjenopprettet fra: themathpage.com.



Ingen har kommentert denne artikkelen ennå.