
Logaritmiske funksjonsegenskaper, eksempler, øvelser
De logaritmisk funksjon er et matematisk forhold som forbinder hvert positive reelle tall x med sin logaritme Y på en base til. Denne relasjonen oppfyller kravene for å være en funksjon: hvert element x som tilhører domenet har et unikt bilde.
Derfor:
f (x) = y = loggtil x , med en> 0 og forskjellig fra 1.
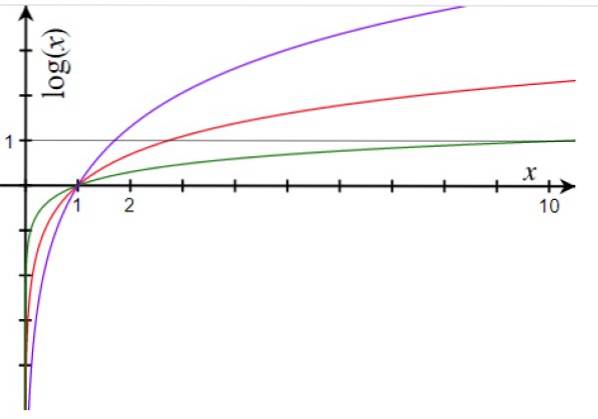
Hovedegenskapene til den logaritmiske funksjonen er:
-Domenet er alle realer større enn 0, inkludert ikke 0. Med andre ord er det ingen logaritme på 0 eller negative tall i noen base. I intervallform:
Sol F = (0, ∞ +)
-Logaritmen til et tall kan være negativ, positiv eller 0, så dets område eller område er:
Rgo F = (-∞, ∞ +)
-Den logaritmiske funksjonen øker alltid for a> 1 og synker for a<1.
-Det omvendte av f (x) = loggtil x er den eksponensielle funksjonen.
Faktisk er logaritmefunksjonen den omvendte funksjonen til den potensielle funksjonen:
F-1(x) = aY
Siden logaritmen i basen til av et tall x, Det er tallet Y som basen skal heves til til å få x.
-Logaritmen til basen er alltid 1. Dermed er grafen til f (x) = loggtil x krysser alltid x-aksen på punktet (1,0)
-Den logaritmiske funksjonen er transcendent og det kan ikke uttrykkes som et polynom eller som en kvotient av disse. I tillegg til logaritmen inkluderer denne gruppen blant annet de trigonometriske og eksponensielle funksjonene.
Artikkelindeks
- 1 Eksempler
- 2 Fordelene med logaritmer
- 2.1 Eksempel
- 3 Søknadsøvelse: Richter-skalaen
- 3.1 Løsning
- 4 Referanser
Eksempler
Den logaritmiske funksjonen kan etableres ved forskjellige baser, men de mest brukte er 10 og og, hvor og er Euler-tallet lik 2.71828 ... .
Når basen 10 brukes, kalles logaritmen en desimal logaritme, vulgær logaritme, Briggs eller bare logaritme.
Og hvis tallet e blir brukt, kalles det en naturlig logaritme, av John Napier, den skotske matematikeren som oppdaget logaritmer..
Notasjonen som brukes for hver enkelt er følgende:
-Desimal logaritme: logg10 x = logg x
-Naturlig logaritme: ln x
Når en annen base skal brukes, er det helt nødvendig å indikere det som et abonnement, fordi logaritmen til hvert tall er forskjellig avhengig av basen som skal brukes. For eksempel, hvis det er logaritmer i base 2, skriv:
y = loggto x
La oss se på logaritmen til tallet 10 i tre forskjellige baser, for å illustrere dette punktet:
logg 10 = 1
ln 10 = 2.30259
Loggto 10 = 3.32193
Vanlige kalkulatorer har bare desimallogaritmer (log-funksjon) og naturlig logaritme (ln-funksjon). På Internett er det kalkulatorer med andre baser. I alle fall kan leseren med hjelp bekrefte at verdiene ovenfor er sanne:
101 = 10
og2.3026 = 10.0001
to3.32193 = 10.0000
Små desimalforskjeller skyldes antall desimaler tatt ved beregning av logaritmen.
Fordelene med logaritmer
Blant fordelene med å bruke logaritmer er den enkle de gir å jobbe med store tall, ved hjelp av logaritmen deres i stedet for tallet direkte.
Dette er mulig fordi logaritmefunksjonen vokser saktere når tallene blir større, som vi kan se i grafen.
Så selv med veldig store tall er logaritmene deres mye mindre, og det er alltid enklere å manipulere små tall..
Videre har logaritmer følgende egenskaper:
-Produkt: logg (a.b) = logg a + logg b
-Quotient: logg (a / b) = logg - logg b
-Makt: logg ab = b.logg a
Og på denne måten blir produktene og kvotientene tillegg og subtraksjoner av mindre tall, mens potensasjonen blir et enkelt produkt selv om kraften er høy..
Derfor tillater logaritmer oss å uttrykke tall som varierer i veldig store verdiområder, for eksempel lydens intensitet, pH i en løsning, lysstyrken til stjerner, den elektriske motstanden og intensiteten til jordskjelv på Richter-skalaen..

La oss se et eksempel på håndtering av egenskapene til logaritmer:
Eksempel
Finn verdien av x i følgende uttrykk:
logg (5x +1) = 1 + logg (2x-1)
Svar
Vi har her en logaritmisk ligning, siden det ukjente er i logaritmens argument. Det løses ved å legge igjen en enkelt logaritme på hver side av likestillingen.
Vi begynner med å plassere alle ordene som inneholder "x" til venstre for likestillingen, og de som bare inneholder tall til høyre:
logg (5x + 1) - logg (2x-1) = 1
Til venstre har vi subtraksjon av to logaritmer, som kan skrives som logaritmen til et kvotient:
logg [(5x + 1) / (2x-1)] = 1
Til høyre er imidlertid tallet 1, som vi kan uttrykke som logg 10, som vi så tidligere. Deretter:
logg [(5x + 1) / (2x-1)] = logg 10
For at likestilling skal oppfylles, argumenter av logaritmene må være like:
(5x + 1) / (2x-1) = 10
5x + 1 = 10 (2x - 1)
5x + 1 = 20 x - 10
-15 x = -11
x = 11/15
Søknadsøvelse: Richter-skalaen
I 1957 skjedde et jordskjelv i Mexico med styrke 7,7 på Richter-skalaen. I 1960 skjedde et nytt jordskjelv av større styrke i Chile, på 9,5.
Beregn hvor mange ganger jordskjelvet i Chile var mer intenst enn det i Mexico, vel vitende om størrelsen MR på Richter-skalaen er den gitt av formelen:
MR = logg (104 JEG)
Løsning
Størrelsen på Richters skala av et jordskjelv er en logaritmisk funksjon. Vi skal beregne intensiteten til hvert jordskjelv, siden vi har Richter-størrelsene. La oss gjøre det trinn for trinn:
-Mexico: 7,7 = logg (104 JEG)
Siden det motsatte av logaritmefunksjonen er det eksponentielle, bruker vi dette på begge sider av likheten med den hensikt å løse for I, som finnes i logaritmens argument..
Siden de er desimallogaritmer, er basen 10. Da:

10 7.7 = 104 Jeg
Intensiteten til jordskjelvet i Mexico var:
JegM = 10 7.7 / 104 = 103.7
-chili: 9,5 = logg (104 JEG)
Den samme prosedyren tar oss til intensiteten av det chilenske jordskjelvet jegCh:
JegCh = 10 9.5 / 104 = 105.5
Nå kan vi sammenligne begge intensitetene:
JegCh / JEGM = 105.5 / 103.7 = 101.8 = 63,1
JegCh = 63,1. JegM
Jordskjelvet i Chile var omtrent 63 ganger mer intenst enn det i Mexico. Siden størrelsen er logaritmisk, vokser den saktere enn intensiteten, så en forskjell på 1 i størrelsen betyr en 10 ganger større amplitude av den seismiske bølgen.
Forskjellen mellom størrelsen på begge jordskjelv er 1,8, derfor kan vi forvente en forskjell i intensiteter nærmere 100 enn til 10, slik det faktisk skjedde..
Faktisk, hvis forskjellen hadde vært nøyaktig 2, ville det chilenske jordskjelvet vært 100 ganger mer intenst enn det meksikanske..
Referanser
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Figuera, J. 2000. Matematikk 1.. Diversifisert år. CO-BO utgaver.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Larson, R. 2010. Beregning av en variabel. 9. plass. Utgave. Mcgraw hill.
- Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Utgave. Cengage læring.



Ingen har kommentert denne artikkelen ennå.