
Definisjon, funksjoner, eksempler
EN surjective funksjon er ethvert forhold der hvert element som tilhører kodene er et bilde av minst ett element i domenet. Også kjent som funksjon på, er en del av klassifiseringen av funksjoner med hensyn til måten elementene deres er relatert til.
For eksempel en funksjon F: A → B definert av F (x) = 2x
Som lyder "F hva med TIL før B definert av F (x) = 2x "
Det er på tide å definere start- og ferdigsett A og B.
A: 1, 2, 3, 4, 5 Nå skal verdiene eller bildene som hvert av disse elementene viser når de blir evaluert i F, vil være elementene i kodene.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Dermed danner helheten B: 2, 4, 6, 8, 10
Det kan da konkluderes med at:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 definert av F (x) = 2x Det er en surjective funksjon
Hvert element i kodene må skyldes minst én operasjon av den uavhengige variabelen gjennom den aktuelle funksjonen. Det er ingen begrensning av bilder, et element i kodene kan være et bilde av mer enn ett element i domenet og fortsatt prøve et surjective funksjon.
Bildet viser 2 eksempler med surjective funksjoner.
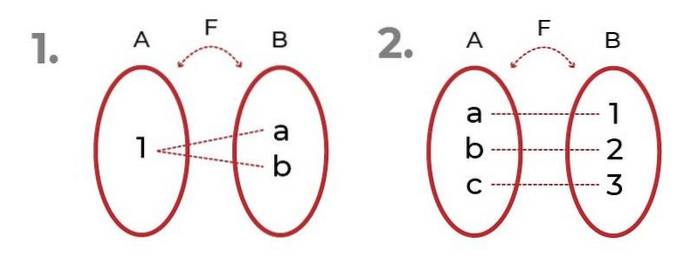
I den første observeres det at bildene kan henvises til det samme elementet, uten at det går på bekostning av surjectivity av funksjonen.
I det andre ser vi en rettferdig fordeling mellom domene og bilder. Dette gir opphav til bijektiv funksjon, der kriteriene for injeksjonsfunksjon og adjektivfunksjon.
En annen metode for å identifisere surjective funksjoner, er å sjekke om kodene er lik funksjonens rekkevidde. Dette betyr at hvis ankomstsettet er lik bildene som tilbys av funksjonen når man vurderer den uavhengige variabelen, funksjonen er adjektiv.
Artikkelindeks
- 1 eiendommer
- 1.1 Funksjonskondisjonering
- 2 Eksempler: løste øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 2.3 Øvelse 3
- 2.4 Øvelse 4
- 2.5 Øvelse 4
- 2.6 Øvelse 5
- 3 Foreslåtte øvelser
- 4 Referanser
Eiendommer
Å overveie surjective til en funksjon må følgende oppfylles:
Være F: DF → CF
∀ b ℮ CF OG til ℮ DF / F (a) = b
Dette er den algebraiske måten å fastslå det på for alle "b" som tilhører CF det er et “a” som tilhører DF slik at funksjonen F evaluert i "a" er lik "b".
Surjektivitet er en egenart ved funksjoner, der kodene og rekkevidden er like. Dermed utgjør elementene som evalueres i funksjonen ankomstsettet.
Funksjonskondisjonering
Noen ganger en funksjon som ikke er det surjective, det kan bli utsatt for visse betingelser. Disse nye forholdene kan gjøre det til et surjective funksjon.
Alle slags modifikasjoner av domenet og kodene til funksjonen er gyldige, der målet er å oppfylle surjektivitetsegenskapene i den tilsvarende relasjonen.
Eksempler: øvelser løst
For å oppfylle vilkårene for surjectivity forskjellige kondisjoneringsteknikker må brukes, dette for å sikre at hvert element i kodene er innenfor settet med bilder av funksjonen.
Øvelse 1
- La funksjonen F: R → R definert av linjen F (x) = 8 - x
A: [Alle reelle tall]
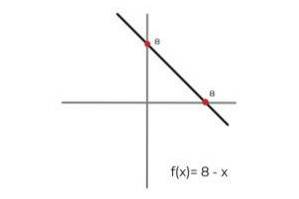
I dette tilfellet beskriver funksjonen en kontinuerlig linje, som dekker alle reelle tall i både domenet og området. Fordi rekkevidden til funksjonen RF tilsvarer kodene R Det kan konkluderes med at:
F: R → R definert av linjen F (x) = 8 - x er en surjective funksjon.
Dette gjelder for alle lineære funksjoner (Funksjoner hvis største grad av variabelen er en).
Øvelse 2
- Studer funksjonen F: R → R definert av F (x) = xto : Definer om det er en surjective funksjon. Hvis ikke, vis forholdene som er nødvendige for å gjøre det til en forventning.
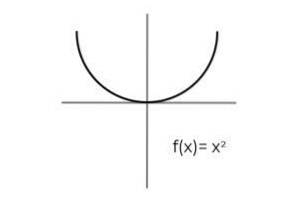
Det første du bør vurdere er kodemannen til F, som består av de reelle tallene R. Det er ingen måte for funksjonen å returnere negative verdier, som ekskluderer de virkelige negativene fra de mulige bildene.
Konditionering av kodene til intervallet [0 , ∞ ]. Det unngås å la elementene i kodene være urelaterte F.
Bildene gjentas for par av elementer av den uavhengige variabelen, for eksempel x = 1 Y x = - 1. Men dette påvirker bare injeksjonsevne av funksjonen, ikke er et problem for denne studien.
På denne måten kan det konkluderes med at:
F: R →[0, ∞ ) definert av F (x) = xto Det er en surjective funksjon
Øvelse 3
- Definer vilkårene for kodene de vil gjøre surjectives til funksjonene
F: R → R definert av F (x) = Sen (x)
F: R → R definert av F (x) = Cos (x)
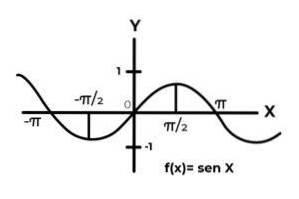
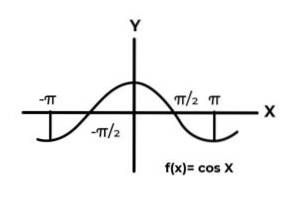
Oppførselen til de trigonometriske funksjonene er lik den for bølger, og det er veldig vanlig å finne repetisjoner av den avhengige variabelen mellom bildene. I de fleste tilfeller er funksjonens rekkevidde begrenset til en eller flere sektorer av den virkelige linjen.
Dette er tilfelle av Sine og Cosine funksjonene. Der deres verdier svinger i intervallet [-1, 1]. Dette intervallet må forutsette kodene for å oppnå funksjonens surjektivitet.
F: R →[-elven] definert av F (x) = Sen (x) Det er en surjective funksjon
F: R →[-elven]definert av F (x) = Cos (x) Det er en adjektivfunksjon
Øvelse 4
- Studer funksjonen
F: [0, ∞ ) → R definert av F (x) = ± √x betegne om det er en surjective funksjon
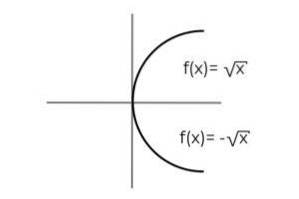
Funksjonen F (x) = ± √x Den har det spesielle at den definerer to avhengige variabler til hver verdi av "x". Det vil si at området mottar to elementer for hver som er laget i domenet. En positiv og negativ verdi må bekreftes for hver verdi av "x".
Når man observerer startsettet, bemerkes det at domenet allerede er begrenset, dette for å unngå ubestemthet som produseres når man vurderer et negativt tall innenfor en jevn rot.
Når du verifiserer funksjonsområdet, bemerkes det at hver verdi av kodene tilhører området.
På denne måten kan det konkluderes med at:
F: [0, ∞ ) → R definert av F (x) = ± √x Det er en surjective funksjon
Øvelse 4
- Studer funksjonen F (x) = Ln x angi om det er en surjective funksjon. Beting ankomst- og avgangssett for å tilpasse funksjonen til surjectivitetskriteriene.
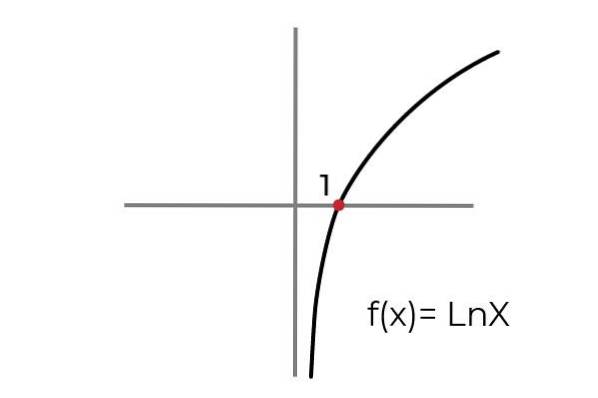
Som vist i grafen funksjonen F (x) = Ln xden er definert for verdier på "x" større enn null. Mens verdiene til "og" eller bildene kan ha noen reell verdi.
På denne måten kan vi begrense domenet til F (x) = til intervall (0 , ∞ )
Så lenge funksjonens rekkevidde kan holdes som settet med reelle tall R.
Med tanke på dette kan det konkluderes med at:
F: [0, ∞ ) → R definert av F (x) = Ln x Det er en surjective funksjon
Øvelse 5
- Studer funksjonen for absolutt verdi F (x) = | x | og angi ankomst- og avgangssett som oppfyller kriteriene for surjektivitet.
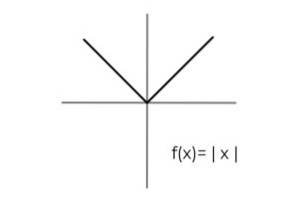
Domenet til funksjonen holder for alle reelle tall R. På denne måten må den eneste betingelsen utføres i kodene, med tanke på at absoluttverdifunksjonen bare tar positive verdier..
Vi fortsetter med å etablere kodene til funksjonen som tilsvarer den til den samme
[0 , ∞ )
Nå kan det konkluderes med at:
F: [0, ∞ ) → R definert av F (x) = | x | Det er en surjective funksjon
Foreslåtte øvelser
- Sjekk om følgende funksjoner er overlappende:
- F: (0, ∞ ) → R definert av F (x) = Logg (x + 1)
- F: R → R definert av F (x) = x3
- F: R →[1, ∞ ) definert av F (x) = xto + 1
- [0, ∞ ) → R definert av F (x) = Logg (2x + 3)
- F: R → R definert av F (x) = Sek x
- F: R - 0 → R definert av F (x) = 1 / x
Referanser
- Introduksjon til logikk og kritisk tenking. Merrilee H. Laks. University of Pittsburgh
- Problemer i matematisk analyse. Piotr Biler, Alfred Witkowski. Universitetet i Wroclaw. Polen.
- Elementer av abstrakt analyse. Mícheál O'Searcoid PhD. Institutt for matematikk. University college Dublin, Beldfield, Dublind 4
- Introduksjon til logikk og metodikk for deduktive vitenskaper. Alfred Tarski, New York Oxford. Oxford University press.
- Prinsipper for matematisk analyse. Enrique Linés Escardó. Redaksjonell Reverté S. A 1991. Barcelona Spania.


Ingen har kommentert denne artikkelen ennå.