
Euklidisk geometrihistorie, grunnleggende konsepter og eksempler

De euklidisk geometri tilsvarer studien av egenskapene til geometriske rom der Euklids aksiomer er oppfylt. Selv om dette begrepet noen ganger brukes til å dekke geometrier som har høyere dimensjoner med lignende egenskaper, er det generelt synonymt med klassisk geometri eller plangeometri..
I III-tallet a. C. Euclid og disiplene hans skrev Elementer, et verk som omfattet datidens matematiske kunnskap utstyrt med en logisk-deduktiv struktur. Siden ble geometri en vitenskap, i utgangspunktet for å løse klassiske problemer og utviklet seg til å være en formativ vitenskap som hjelper til å resonnere..

Artikkelindeks
- 1 Historie
- 2 grunnleggende
- 2.1 Vanlige forestillinger
- 2.2 Postulater eller aksiomer
- 3 eksempler
- 3.1 Første eksempel
- 3.2 Andre eksempel
- 3.3 Tredje eksempel
- 4 Referanser
Historie
For å snakke om historien til euklidisk geometri, er det viktig å starte med euklid av Alexandria og Elementer.
Da Egypt ble igjen i hendene på Ptolemaios I, etter Alexander den store død, begynte han sitt prosjekt på en skole i Alexandria.
Blant vismennene som underviste på skolen var Euklid. Det spekuleres i at fødselen hans stammer fra omtrent 325 f.Kr. C. og hans død 265 a. C. Vi kan med sikkerhet vite at han gikk på Platons skole.
I mer enn tretti år underviste Euclid i Alexandria og bygde sine berømte elementer: han begynte å skrive en uttømmende beskrivelse av matematikken i sin tid. Euklids lære ga utmerkede disipler, som Archimedes og Apollonius av Perga.
Euclid var tiltalt for å strukturere de forskjellige oppdagelsene til de gamle grekerne i Elementer, men i motsetning til sine forgjengere begrenser den seg ikke til å bekrefte at en teorem er sant; Euclid tilbyr en demonstrasjon.
De Elementer de er et kompendium med tretten bøker. Etter Bibelen er det den mest utgitte boka, med mer enn tusen utgaver.
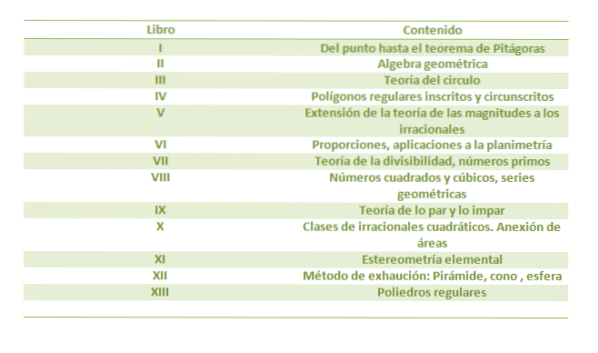
De Elementer er Euklids mesterverk innen geometri, og tilbyr en endelig behandling av geometrien til to dimensjoner (planet) og tre dimensjoner (rom), dette er opprinnelsen til det vi nå kjenner som euklidisk geometri.
Enkle konsepter
Elementene består av definisjoner, vanlige forestillinger og postulater (eller aksiomer) etterfulgt av teoremer, konstruksjoner og bevis..
- Et poeng er det som ikke har deler.
- En linje er en lengde uten bredde.
- En rett linje er en som ligger likt i forhold til punktene som er i dette.
- Hvis to linjer er kuttet slik at de tilstøtende vinklene er like, kalles vinklene rette vinkler og linjene kalles vinkelrett.
- Parallelle linjer er de som, når de er i samme plan, aldri krysser hverandre.
Etter disse og andre definisjoner presenterer Euclid oss en liste med fem postulater og fem forestillinger..
Vanlige forestillinger
- To ting som er lik en tredjedel er like hverandre.
- Hvis de samme tingene blir lagt til de samme tingene, er resultatene de samme.
- Hvis like ting trekkes fra like ting, er resultatene like.
- Ting som samsvarer med hverandre er like hverandre.
- Totalen er større enn en del.
Postulater eller aksiomer
- Én og bare en linje går gjennom to forskjellige punkter.
- Rette linjer kan utvides på ubestemt tid.
- En sirkel kan tegnes med hvilket som helst senter og hvilken som helst radius.
- Alle rette vinkler er like.
- Hvis en rett linje krysser to rette linjer, slik at de innvendige vinklene på samme side blir mindre enn to rette vinkler, vil de to linjene krysse på den siden..
Dette siste postulatet er kjent som det parallelle postulatet, og det ble omformulert som følger: "For et punkt utenfor en linje kan det trekkes en parallell til den gitte linjen".
Eksempler
Her er noen teoremer om Elementer de skal tjene til å vise egenskaper til geometriske rom der de fem postulatene til Euklid oppfylles; I tillegg vil de illustrere den logisk-deduktive resonnementet som denne matematikeren brukte.
Første eksempel
Proposisjon 1.4. (LAL)
Hvis to trekanter har to sider og vinkelen mellom dem er like, så er de andre sidene og de andre vinklene like..
Demonstrasjon
La ABC og A'B'C 'være to trekanter med AB = A'B', AC = A'C 'og vinklene BAC og B'A'C' er like. La oss flytte trekanten A'B'C 'slik at A'B' sammenfaller med AB og den vinkelen B'A'C 'sammenfaller med vinkelen BAC.
Så linje A'C 'sammenfaller med linje AC, slik at C' sammenfaller med C. Deretter, etter postulat 1, må linje BC falle sammen med linje B'C '. Derfor sammenfaller de to trekantene, og følgelig er vinklene og sidene like.
Andre eksempel
Proposisjon 1.5. (Pons Asinorum)
Hvis en trekant har to like sider, er de motsatte vinklene til disse sidene like..
Demonstrasjon
Anta at trekanten ABC har like sider AB og AC.
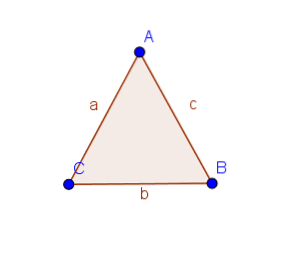
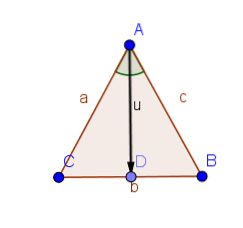
Så trekantene ABD og ACD har to like sider, og vinklene mellom dem er like. Således, ved proposisjon 1.4, er vinklene ABD og ACD like.
Tredje eksempel
Proposisjon 1.31
Du kan konstruere en linje parallelt med en linje gitt av et gitt punkt.
Bygning
Gitt en linje L og et punkt P, trekkes en linje M gjennom P og krysser L. Deretter trekkes en linje N gjennom P som krysser L. Nå trekkes en linje N gjennom P som krysser M, og danner en vinkel lik den som L danner med M.

Bekreftelse
N er parallell med L.
Demonstrasjon
Anta at L og N ikke er parallelle og krysser ved et punkt A. La B være et punkt i L utover A. Tenk på linjen O som passerer gjennom B og P. Deretter krysser O M i vinkler som legger opp til mindre enn to rett.
Så med 1,5 må linjen O skjære linjen L på den andre siden av M, så L og O krysser hverandre på to punkter, noe som strider mot Postulat 1. Derfor må L og N være parallelle.
Referanser
- Euklidiske elementer av geometri. Det nasjonale autonome universitetet i Mexico
- Euklid. De seks første bøkene og den ellevte og tolvte av Euklids elementer
- Eugenio Filloy Yague. Didaktikk og historie med euklidisk geometri, Grupo Editorial Iberoamericano
- K. Ribnikov. Matematikkens historie. Mir Editorial
- Viloria, N., & Leal, J. (2005) Plane Analytical Geometry. Redaksjonelt Venezolana C.A.


Ingen har kommentert denne artikkelen ennå.