Magnetiske induksjonsformler, hvordan det beregnes og eksempler

De magnetisk induksjon eller magnetisk flytdensitet er en endring av miljøet forårsaket av tilstedeværelsen av elektriske strømmer. De endrer naturen til rommet som omgir dem, og skaper en landsbygda vektor.

Vektoren magnetisk induksjon, magnetisk flytdensitet Eller rett og slett magnetfelt B, den har tre karakteristiske egenskaper: en intensitet uttrykt med en numerisk verdi, en retning og også en sans gitt på hvert punkt i rommet. Den er uthevet med fet skrift for å skille den fra rent numeriske eller skalære mengder.

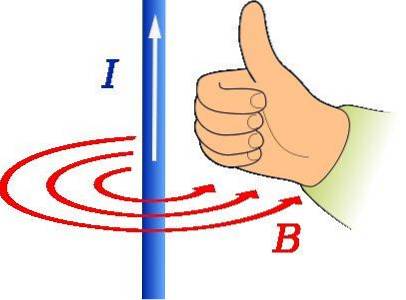
Høyre tommelfingerregel brukes til å finne retningen og retningen til magnetfeltet forårsaket av en strømførende ledning, som vist i figuren ovenfor.

Tommelen på høyre hånd skal peke i strømens retning. Deretter indikerer rotasjonen av de fire gjenværende fingrene formen på B, som i figuren er representert av de konsentriske røde sirkler.

I et slikt tilfelle, adressen til B er tangensiell til omkretsen konsentrisk med ledningen og er mot klokken.

De magnetisk induksjon B I det internasjonale systemet måles Tesla (T), men det er oftere å måle det i en annen enhet kalt Gauss (G). Begge enhetene ble kåret henholdsvis til ære for Nikola Tesla (1856-1943) og Carl Friedrich Gauss (1777-1855) for deres ekstraordinære bidrag til vitenskapen om elektrisitet og magnetisme..

Artikkelindeks

• 1 Hva er egenskapene til magnetisk induksjon eller magnetisk flytdensitet?
• 2 Biot-Savarts lov
• 3 formler
• 4 Hvordan beregnes det?
  • 4.1 Eksempel
• 5 Referanser

Hva er egenskapene til magnetisk induksjon eller magnetisk flytdensitet?

Et kompass som er plassert i nærheten av strømførende ledning vil alltid stemme overens med B. Den danske fysikeren Hans Christian Oersted (1777-1851) var den første som la merke til dette fenomenet tidlig på 1800-tallet.

Og når strømmen opphører, peker kompasset igjen mot geografisk nord, som alltid. Ved å endre kompassets posisjon nøye, oppnås et kart over magnetfeltets form.

Dette kartet er alltid i form av sirkler konsentriske til ledningen, som beskrevet i begynnelsen. På denne måten kan du visualisere B.

Selv om ledningen ikke er rett, vektoren B den vil danne konsentriske sirkler rundt den. For å bestemme formen på feltet, kan du bare forestille deg veldig små ledningssegmenter, så små at de ser rett ut og er omgitt av konsentriske sirkler..

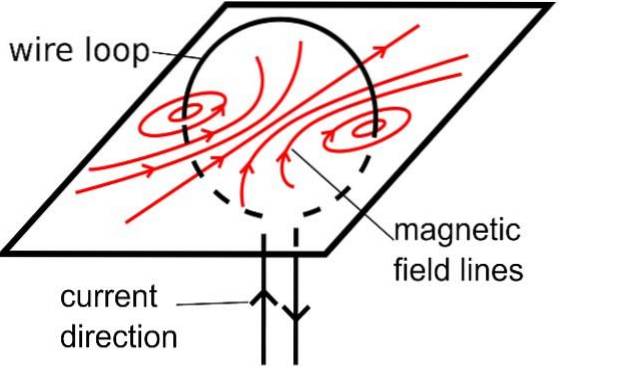
Dette peker på en viktig egenskap av magnetfeltlinjer. B: de har ingen begynnelse eller slutt, de er alltid lukkede kurver.

Biot-Savarts lov

1800-tallet markerte begynnelsen på tiden for elektrisitet og magnetisme i vitenskapen. Rundt året 1820 oppdaget de franske fysikerne Jean Marie Biot (1774-1862) og Felix Savart (1791-1841) loven som bærer navnet deres, og som lar oss beregne vektoren B.

De gjorde følgende observasjoner om bidraget til magnetfeltet produsert av et ledningssegment med differensiell lengde dl som bærer en elektrisk strøm Jeg:

• Størrelsen på B avtar med den omvendte firkanten av avstanden til ledningen (dette er fornuftig: borte fra ledningen intensiteten av B må være mindre enn nær punkter).
• Størrelsen på B er proporsjonal med intensiteten til strømmen Jeg som går gjennom ledningen.
• Adressen til B er tangensiell for radiusomkretsen r sentrert på ledningen og sansen for B er gitt, som vi sa, av regelen om høyre tommel.

Tverrproduktet eller tverrproduktet er det passende matematiske verktøyet for å uttrykke det siste punktet. For å etablere et vektorprodukt trengs to vektorer, som er definert som følger:

• dl er vektoren hvis størrelse er lengden på differensialsegmentet dl
• r er vektoren som går fra ledningen til det punktet hvor du vil finne feltet

Formler

Alt dette kan kombineres til et matematisk uttrykk:

Konstanten av proporsjonalitet som er nødvendig for å etablere likeverd er magnetisk permeabilitet av ledig plass μ_eller  = 4π.10^-7 T.m / A

Dette uttrykket er Biot og Savart-loven, som lar oss beregne magnetfeltet til et nåværende segment.

Et slikt segment må igjen være en del av en større og mer lukket krets: en strømfordeling.

Forutsetningen om at kretsen er lukket er nødvendig for at en elektrisk strøm skal kunne strømme. Elektrisk strøm kan ikke strømme i åpne kretser.

Til slutt, for å finne det totale magnetiske feltet for nevnte strømfordeling, blir alle bidragene til hvert differensialsegment lagt til dl. Dette tilsvarer integrering over hele distribusjonen:

For å anvende Biot-Savart-loven og beregne den magnetiske induksjonsvektoren, er det nødvendig å vurdere noen veldig viktige viktige punkter:

• Tverrproduktet mellom to vektorer resulterer alltid i en annen vektor.

• 

• Det er praktisk å finne vektorproduktet før for å overføre til oppløsningen til integralet, så løses integralet av hver av komponentene oppnådd separat.
• Det er nødvendig å tegne et bilde av situasjonen og etablere et passende koordinatsystem.
• Når det forekommer noen symmetri, bør den brukes til å spare beregningstid.
• Når det er trekanter, er den pythagoreiske teoremet og cosinussetningen til stor hjelp for å etablere det geometriske forholdet mellom variablene.

Hvordan beregnes det?

Med et praktisk eksempel på beregning av B for en rett ledning, gjelder disse anbefalingene.

Eksempel

Beregn magnetfeltvektoren som en veldig lang rettlinjetråd produserer ved et punkt P i rommet, i henhold til figuren vist.

Fra figuren må du:

• Ledningen er rettet i vertikal retning, med strøm I som strømmer oppover. Denne retningen er + y i koordinatsystemet, hvis opprinnelse er ved punkt O.

• 

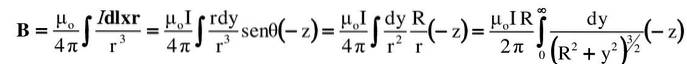
• I et slikt tilfelle, i henhold til regelen om høyre tommel, B på punkt P er det rettet mot innsiden av papiret, det er derfor det er betegnet med en liten sirkel og et "x" i figuren. Denne adressen blir tatt som -z.
• Den rette trekanten hvis ben er Y Y R, relatere begge variablene i henhold til Pythagoras teorem: r^to= R^to+Y^to

Alt dette er erstattet i integralen. Tverrproduktet eller krysset er angitt med sin størrelse pluss retning og dens sans:

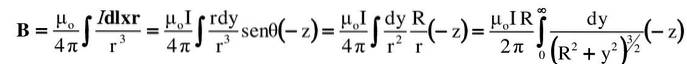
Den foreslåtte integralen finnes i en tabell over integraler, eller den løses ved en passende trigonometrisk erstatning (leseren kan sjekke resultatet ved hjelp av y = Rtg θ):

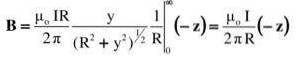
Resultatet stemmer overens med det som var forventet: feltets størrelse avtar med avstanden R og øker proporsjonalt med intensiteten til strømmen I.

Selv om en uendelig lang ledning er en idealisering, er uttrykket oppnådd en veldig god tilnærming for feltet av en lang ledning..

Med Biot og Savarts lov er det mulig å finne magnetfeltet til andre høysymmetriske distribusjoner, for eksempel en sirkulær sløyfe som bærer strøm eller bøyde ledninger som kombinerer rettlinjede og krøllete segmenter..

Selvfølgelig, for å analytisk løse den foreslåtte integralen, må problemet ha en høy grad av symmetri. Ellers er alternativet å løse integralet numerisk.

Referanser

1. Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 2. Mexico. Cengage Learning Editors. 367-372.