
Konvergerende linseegenskaper, typer og løst trening
De konvergerende linser Det er de som er tykkere i den midtre delen og tynnere i kantene. Som en konsekvens konsentrerer (konvergerer) de lysstrålene som faller på dem parallelt med hovedaksen på et enkelt punkt. Dette punktet kalles fokus, eller bildefokus, og er representert med bokstaven F. Konvergerende eller positive linser danner det som kalles virkelige bilder av gjenstander..
Et typisk eksempel på en konvergerende linse er et forstørrelsesglass. Imidlertid er det vanlig å finne denne typen linser i mye mer komplekse enheter som mikroskop eller teleskoper. Faktisk er et grunnleggende sammensatt mikroskop et som består av to konvergerende linser som har liten brennvidde. Disse linsene kalles objektive og okulære.

Konvergerende linser brukes i optikk til forskjellige bruksområder, selv om det kanskje er mest kjent å korrigere synsfeil. Dermed er de indikert for å behandle hyperopi, presbyopi og også noen typer astigmatisme som hyperopisk astigmatisme.
Artikkelindeks
- 1 Funksjoner
- 2 Konvergerende linseelementer
- 3 Bildedannelse i konvergerende linser
- 4 typer konvergerende linser
- 5 Forskjell med divergerende linser
- 6 Gaussiske ligninger av tynne linser og forstørrelse av en linse
- 6.1 Gaussisk ligning
- 6.2 Forstørre et objektiv
- 7 Øvelse løst
- 8 Referanser
Kjennetegn
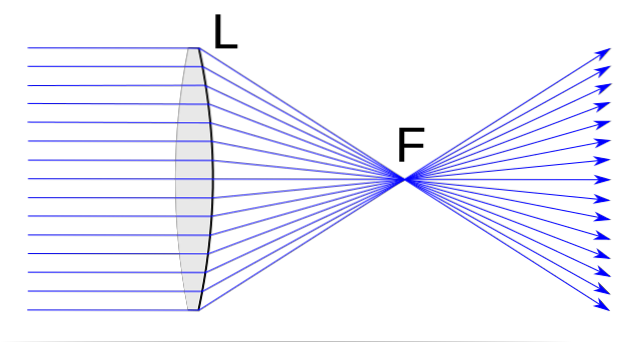
Konvergerende linser har en rekke definerende egenskaper. I alle fall er det kanskje den viktigste vi allerede har avansert i definisjonen. Dermed er konvergerende linser preget av å avbøye enhver stråle som faller på dem i fokus parallelt med hovedaksen.
Videre, gjensidig, brytes enhver innfallende stråle som passerer fokus parallelt med den optiske aksen til linsen..
Konvergerende linseelementer
For studien er det viktig å vite hvilke elementer som utgjør linser generelt og konvergerende linser spesielt..
Generelt kalles det det optiske sentrum for en linse til det punktet hvor hver stråle som passerer gjennom den ikke opplever noe avvik..
Hovedaksen er linjen som forbinder det optiske sentrum, og hovedfokuset, som vi allerede har kommentert, er representert med bokstaven F.
Hovedfokuset er punktet der alle strålene som treffer linsen er parallelle med hovedaksen..
Brennvidden er avstanden mellom det optiske sentrum og fokuset..
Krumningssentrene er definert som sentrene til kulene som lager linsen; krumningsradiene er radiene til kulene som gir opphav til linsen.
Og til slutt kalles linsens sentrale plan det optiske planet..
Bildedannelse i konvergerende linser
Når det gjelder dannelsen av bilder i konvergerende linser, må en rekke grunnleggende regler tas i betraktning, som forklares nedenfor..
Hvis strålen treffer linsen parallelt med aksen, konvergerer den nye strålen på bildefokuset. Omvendt, hvis en hendelsesstråle passerer gjennom objektfokuset, kommer strålen frem i en retning parallell med aksen. Til slutt brytes strålene som går gjennom det optiske senteret uten å oppleve noen form for avbøyning..
Som en konsekvens kan følgende situasjoner oppstå i en konvergerende linse:
- At objektet er plassert i forhold til det optiske planet i en avstand større enn dobbelt brennvidde. I dette tilfellet er det produserte bildet ekte, invertert og mindre enn objektet..
- At objektet er plassert i en avstand fra det optiske planet som tilsvarer det dobbelte av brennvidden. Når dette skjer, er bildet som oppnås, et reelt bilde, invertert og i samme størrelse som objektet.
- At objektet er i en avstand fra det optiske planet mellom en og to brennvidder. Deretter produseres et bilde som er ekte, invertert og større enn det opprinnelige objektet..
- At objektet er plassert i en avstand fra det optiske planet som er mindre enn brennvidden. I så fall vil bildet være virtuelt, direkte og større enn objektet.
Typer av konvergerende linser
Det er tre forskjellige typer konvergerende linser: bikonvekse linser, plano-konvekse linser og konkave-konvekse linser..
Biconvex linser, som navnet antyder, består av to konvekse overflater. Konvekse fly har i mellomtiden en flat og en konveks overflate. Og til slutt består konkave konvekse linser av en litt konkav og en konveks overflate..
Forskjell med divergerende linser

Divergerende linser, derimot, skiller seg fra konvergerende linser ved at tykkelsen avtar fra kantene mot midten. Dermed, i motsetning til hva som skjedde med konvergerende linser, blir lysstrålene som treffer parallelt med hovedaksen i denne typen linser skilt. På denne måten danner de det som kalles virtuelle bilder av objekter.
I optikk brukes divergerende eller negative linser, som de også er kjent, hovedsakelig for å korrigere nærsynthet.
Gaussiske ligninger av tynne linser og forstørrelse av et objektiv
Generelt er typen linser som studeres det som kalles tynne linser. Disse er definert som de som har en liten tykkelse sammenlignet med krumningsradiene på overflatene som begrenser dem.
Denne typen linser kan studeres med den Gaussiske ligningen og med ligningen som gjør det mulig å bestemme forstørrelsen til et objektiv.
Gauss-ligning
Den Gaussiske ligningen for tynne linser kan brukes til å løse mange problemer innen grunnleggende optikk. Derav dens store betydning. Uttrykket er følgende:
1 / f = 1 / p + 1 / q
Hvor 1 / f er det som kalles kraften til en linse og f er brennvidden eller avstanden fra det optiske sentrum til fokus F. Måleenheten for en linses kraft er diopteren (D), hvor 1 D = 1 m-1. På den annen side er p og q henholdsvis avstanden som et objekt er lokalisert til og avstanden som dets bilde blir observert.
Forstørrelse av et objektiv
Den laterale forstørrelsen av en tynn linse oppnås med følgende uttrykk:
M = - q / p
Hvor M er forstørrelsen. Fra verdien av økningen kan en rekke konsekvenser trekkes:
Ja | M | > 1, størrelsen på bildet er større enn objektet
Ja | M | < 1, el tamaño de la imagen es menor que el del objeto
Hvis M> 0 er bildet riktig og på samme side av linsen som objektet (virtuelt bilde)
Ja M < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)
Treningen løst
En kropp er plassert en meter fra en konvergerende linse, som har en brennvidde på 0,5 meter. Hvordan vil kroppsbildet se ut? Hvor langt borte vil du være?
Vi har følgende data: p = 1 m; f = 0,5 m.
Vi plugger disse verdiene i den Gaussiske ligningen for tynne linser:
1 / f = 1 / p + 1 / q
Og følgende gjenstår:
1 / 0,5 = 1 + 1 / q; 2 = 1 + 1 / q
Vi isolerer 1 / q
1 / q = 1
For å løse for q og få:
q = 1
Derfor erstatter vi i ligningen forstørrelsen av en linse:
M = - q / p = -1 / 1 = -1
Derfor er bildet reelt siden q> 0, invertert fordi M < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.
Referanser
- Lys (n.d.). På Wikipedia. Hentet 18. mars 2019 fra es.wikipedia.org.
- Lekner, John (1987). Teori om refleksjon, om elektromagnetiske og partikkelbølger. Springer.
- Lys (n.d.). I Wikipedia. Hentet 20. mars 2019 fra en.wikipedia.org.
- Linse (n.d.). På Wikipedia. Hentet 17. mars 2019 fra es.wikipedia.org.
- Objektiv (optikk). I Wikipedia. Hentet 19. mars 2019 fra en.wikipedia.org.
- Hecht, Eugene (2002). Optikk (4. utg.). Addison Wesley.
- Tipler, Paul Allen (1994). Fysisk. 3. utgave. Barcelona: Jeg snudde meg.



Ingen har kommentert denne artikkelen ennå.