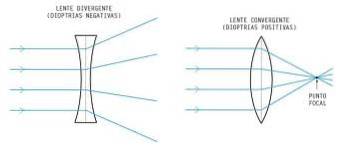
De divergerende linser De er de som er tynnere i den sentrale delen og tykkere i kantene. Som en konsekvens skiller de (avviker) lysstrålene som treffer dem parallelt med hovedaksen. Forlengelsene sine ender sammen i bildefokuset til venstre for linsen.
Ulike linser, eller negative som de også er kjent, danner det som kalles virtuelle bilder av objekter. De har forskjellige applikasjoner. Spesielt i oftalmologi brukes de til å korrigere nærsynthet og noen typer astigmatisme.
Så hvis du er nærsynt og bruker briller, har du et perfekt eksempel på en divergerende linse for hånden..
Artikkelindeks
Som forklart tidligere er divergerende linser smalere i sin sentrale del enn ved kantene. I tillegg er i denne typen linser alltid en av overflatene konkave. Dette gir denne typen linser en rekke egenskaper.
Til å begynne med resulterer forlengelsen av strålene som påvirker dem i virtuelle bilder som ikke kan samles på noen form for skjerm. Dette er slik, fordi strålene som passerer gjennom linsen ikke konvergerer på noe tidspunkt, siden de divergerer i alle retninger. I tillegg, avhengig av linsens krumning, vil strålene åpne i større eller mindre grad..
En annen viktig egenskap ved denne typen linser er at fokuset er til venstre for linsen, slik at det er mellom det og objektet..
I tillegg, i divergerende linser, er bildene mindre enn objektet og ligger mellom objektet og fokuset..
Når du studerer dem, er det viktig å vite hvilke elementer som utgjør linser generelt og divergerende linser spesielt..
Punktet der strålene ikke avbøyes, kalles det optiske senteret til en linse. Hovedaksen på sin side er linjen som går sammen med nevnte punkt og hovedfokus, hvor sistnevnte er representert med bokstaven F.
Navnet på hovedfokuset er det punktet hvor alle strålene som treffer linsen finnes parallelt med hovedaksen..
På denne måten kalles avstanden mellom det optiske sentrum og fokus brennvidden..
Krumningssentrene er definert som sentrene til kulene som lager linsen; Krumningsradiene er dermed radiusene til kulene som gir opphav til linsen. Og til slutt kalles linsens sentrale plan det optiske planet.For å grafisk bestemme dannelsen av et bilde i en tynn linse, er det bare nødvendig å vite retningen som to av de tre strålene vil følge
hvis bane er kjent.
En av dem er den som treffer linsen parallelt med linsens optiske akse. Dette, når det er brutt i linsen, vil passere gjennom bildefokuset. Den andre av strålene hvis vei er kjent, er den gjennom det optiske sentrum. Dette vil ikke se banen endret.
Den tredje og siste er den som passerer gjennom objektfokuset (eller forlengelsen krysser objektfokuset) som etter refraksjon vil følge en retning parallell med den optiske aksen til linsen..
På denne måten vil generelt en eller annen type bilde dannes i linsene avhengig av posisjonen til objektet eller kroppen i forhold til linsen..
Imidlertid, i det spesielle tilfellet med divergerende linser, uansett kroppens posisjon foran linsen, vil bildet som skal dannes ha visse egenskaper. Og det er at i divergerende linser vil bildet alltid være virtuelt, mindre enn kroppen og riktig.
Det faktum at de kan skille lyset som passerer gjennom dem, gir divergerende linser noen interessante kvaliteter innen optikk. På denne måten kan de korrigere nærsynthet og noen spesifikke typer astigmatisme.
Divergerende oftalmiske linser skiller lysstrålene slik at de er lenger fra hverandre når de når menneskets øye. Når de krysser hornhinnen og linsen, går de lenger og kan nå netthinnen og forårsake synsproblemer hos personer med nærsynthet..
Som vi allerede har diskutert, har konvergerende linser minst en konkav overflate. På grunn av dette er det tre typer divergerende linser: biconcave, plano-konkav og konveks-konkav..
Divergerende bikonkave linser består av to konkave overflater, plano-konkave linser har en konkav og en flat overflate, mens i konveks-konkav eller divergerende menisk er den ene overflaten litt konveks og den andre er konkav..
I konvergerende linser, i motsetning til hva som skjer i divergerende linser, reduseres tykkelsen fra midten mot kantene. I denne typen linser konsentreres eller konvergerer lysstrålene som faller parallelt med hovedaksen på et enkelt punkt (i fokus). På denne måten lager de alltid ekte bilder av gjenstandene.
I optikk brukes konvergente eller positive linser hovedsakelig for å korrigere hyperopi, presbyopi og noen typer astigmatisme.
Den typen linser som oftest blir studert, kalles tynne linser. Dette definerer alle linser hvis tykkelse er veldig liten sammenlignet med krumningsradiene på overflatene som begrenser dem..
Studien av denne typen linser kan utføres hovedsakelig gjennom to ligninger: den Gaussiske ligningen og ligningen som gjør det mulig å bestemme forstørrelsen av linsen..
Betydningen av den Gaussiske ligningen for tynne linser ligger i det store antallet grunnleggende optiske problemer som det lar seg løse. Uttrykket er følgende:
1 / f = 1 / p + 1 / q
Der 1 / f er kraften til linsen og f er brennvidden eller avstanden fra det optiske sentrum til fokus F. Måleenheten for en linses styrke er diopteren (D), verdien er 1 D = 1 m-1. På den annen side er henholdsvis p og q avstanden som et objekt er lokalisert til og avstanden det blir observert av.
En kropp er plassert 40 centimeter fra en divergerende linse på -40 centimeter brennvidde. Beregn høyden på bildet hvis høyden på objektet er 5 cm. Bestem også om bildet er rett eller invertert.
Vi har følgende data: h = 5 cm; p = 40 cm; f = -40 cm.
Disse verdiene er erstattet i den gaussiske ligningen for tynne linser:
1 / f = 1 / p + 1 / q
Og du får:
1 / -40 = 1/40 + 1 / q
Fra hvor q = - 20 cm
Deretter erstatter vi resultatet oppnådd tidligere i ligningen for forstørrelse av en linse:
M = - q / p = - -20 / 40 = 0,5
Å oppnå at verdien av økningen er:
M = h '/ h = 0,5
Å løse for h ', som er verdien av høyden på bildet, får vi:
h '= h / 2 = 2,5 cm.
Bildens høyde er 2,5 cm. Dessuten er bildet rett siden M> 0 og redusert siden absoluttverdien til M er mindre enn 1.
Ingen har kommentert denne artikkelen ennå.