De Coulomb lov det er den fysiske loven som styrer samspillet mellom elektrisk ladede gjenstander. Det ble bekjentgjort av den franske forskeren Charles Augustin de Coulomb (1736-1806), takket være resultatene av hans eksperimenter med torsjonsbalansen.
I 1785 eksperimenterte Coulomb utallige tider med små elektrisk ladede kuler, for eksempel å flytte to kuler nærmere eller lenger fra hverandre, og varierte størrelsen på ladningen og også deres tegn. Observer og registrer alltid hvert svar nøye.
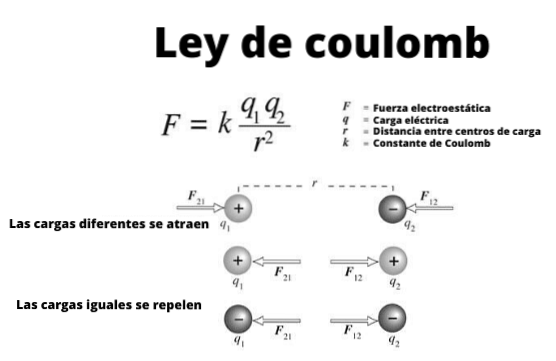
Disse små kulene kan betraktes som punktbelastning, det vil si objekter hvis dimensjoner er ubetydelige. Og de oppfyller, som det er kjent siden de gamle grekernes tid, at ladninger av samme tegn frastøter og de av et annet tegn tiltrekker seg..
Med dette i tankene fant Charles Coulomb følgende:
-Den attraktive eller frastøtende kraften mellom topunktsladninger er direkte proporsjonal med produktet av ladningens størrelse.
-Denne styrken er alltid rettet langs linjen som slutter seg til anklagene.
-Til slutt er kraftens størrelse omvendt proporsjonal med kvadratet av avstanden mellom ladningene.
Artikkelindeks
Takket være disse observasjonene konkluderte Coulomb med at størrelsen på styrken F mellom to punkts kostnader hva1 Y hvato, skilt en avstand r, er matematisk gitt som:
Siden kraften er en vektorstørrelse, defineres en enhetsvektor for å uttrykke den fullstendig r i retning av linjen som forbinder ladningene (en enhetsvektor har størrelsesorden lik 1).
I tillegg kalles den proporsjonalitetskonstanten som er nødvendig for å transformere det forrige uttrykket til en likhet, kog eller bare k: den elektrostatisk konstant eller Coulomb er konstant.
Til slutt er Coulombs lov etablert for poenggebyr, gitt av:
Kraft, som alltid i International System of Units, kommer i newton (N). Når det gjelder anklagene, heter enheten coulomb (C) til ære for Charles Coulomb, og til slutt kommer avstanden r i meter (m).
Ser vi nøye på ovenstående ligning, er det klart at den elektrostatiske konstanten må ha enheter N.mto / Cto, for å få newton som et resultat. Verdien av konstanten ble bestemt eksperimentelt som:
kog = 8,89 x 10 9 N.mto / Cto ≈ 9 x 10 9 N.mto / Cto
Figur 1 illustrerer samspillet mellom to elektriske ladninger: når de har samme tegn, frastøter de, ellers tiltrekker de seg.
Merk at Coulombs lov er i samsvar med Newtons tredje lov eller handlings- og reaksjonslov, derfor størrelsen på F1 Y Fto de er de samme, retningen er den samme, men sansene er motsatte.
For å løse problemer med interaksjoner mellom elektriske ladninger, må følgende tas i betraktning:
- Ligningen gjelder utelukkende når det gjelder punktladninger, det vil si elektrisk ladede gjenstander, men med svært små dimensjoner. Hvis de lastede objektene har målbare dimensjoner, er det nødvendig å dele dem i veldig små belastninger og deretter legge til bidragene til hver av disse lastene, som det kreves en integrert beregning for..
- Den elektriske kraften er en vektormengde. Hvis det er mer enn to samvirkende ladninger, vil nettokraften på ladningen qJeg er gitt av superposisjonsprinsippet:
Fnett = Fi1 + Fi2 + Fi3 + Fi4 +… = ∑ Fij
Hvor abonnementet j er lik 1, 2, 3, 4 ... og representerer hver av de gjenværende ladningene.
- Du bør alltid være i samsvar med enhetene. Det hyppigste er å jobbe med den elektrostatiske konstanten i SI-enheter, da er det nødvendig å sørge for at ladningene er i coulomb og avstandene i meter.
- Til slutt gjelder ligningen når ladningene er i statisk likevekt.
I den følgende figuren er det topunktsladninger + q og + 2q. En tredje punktladning -q plasseres ved P. Det blir bedt om å finne den elektriske kraften på denne ladningen på grunn av tilstedeværelsen av de andre.
Det første er å etablere et passende referansesystem, som i dette tilfellet er den horisontale aksen eller x-aksen. Opprinnelsen til et slikt system kan være hvor som helst, men for enkelhets skyld vil det plasseres på P, som vist i figur 4a:
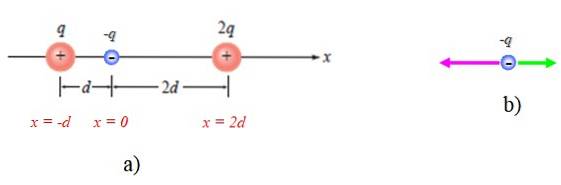
Et diagram over kreftene på -q er også vist, idet man tar i betraktning at den tiltrekkes av de to andre (figur 4b).
La oss ringe F1 kraften som utøves av ladning q på ladning -q, er rettet langs x-aksen og peker i negativ retning, derfor:
Analogt beregnes det Fto:
Merk at størrelsen på Fto er halvparten av det for F1, selv om belastningen er dobbelt. For å finne nettokraften, til slutt tilsettes de vektorielt F1 Y Fto:
Fnett = (-k + k / 2). (qto / dto) (x) N = - (k / 2). (Qto / dto) (x) N
To polystyrenkuler med samme masse m = 9,0 x 10-8 kg har samme positive ladning Q og er suspendert av en silketråd med lengden L = 0,98 m. Kulene er atskilt med en avstand på d = 2 cm. Beregn verdien av Q.
Uttalelsessituasjonen er beskrevet i figur 5a.
Vi velger en av kulene, og på den tegner vi det isolerte kroppsdiagrammet, som inkluderer tre krefter: vekt W, spenning i tauet T og elektrostatisk frastøting F, slik det ser ut i figur 5b. Og nå trinnene:
Verdien av θ / 2 beregnes med trekanten i figur 5c:
θ / 2 = lysbue (1 x 10-to/0,98) = 0,585º
Deretter må vi bruke Newtons andre lov og sette den lik 0, siden ladningene er i statisk likevekt. Viktigere, spenningen T er skrå og har to komponenter:
∑Fx = -T.sin θ + F = 0
∑FY = T.cos θ - W = 0
Vi løser størrelsen på spenningen fra den siste ligningen:
T = W / cos θ = mg / cos θ
Denne verdien erstattes av den første ligningen for å finne størrelsen på F:
F = T sin θ = mg (sin θ / cos θ) = mg. tg θ
Siden F = k Qto / dto, tømmer Q:
Q = 2 × 10-elleve C.
Det er enkelt å kontrollere Coulombs lov ved å bruke en torsjonsbalanse som den som Coulomb brukte i laboratoriet sitt..
Det er to små hyllebærkuler, hvorav den ene i midten av vekten er opphengt av en tråd. Eksperimentet består i å berøre de utslippte hyllebærkulene med en annen metallkule ladet med Q-ladning.
Straks fordeles ladningen likt mellom de to hyllebærkulene, men da de er ladninger av samme tegn, frastøter de hverandre. En kraft virker på den suspenderte sfæren som forårsaker vridning av tråden som den henger fra og umiddelbart beveger seg bort fra den faste sfæren.
Så ser vi at den svinger noen ganger til den når likevekt. Deretter balanseres torsjonen på stangen eller tråden som holder den av den elektrostatiske frastøtningskraften.
Hvis kulene opprinnelig var på 0 °, vil den bevegelige kulen nå ha rotert en vinkel θ. Rundt skalaen er det et bånd gradert i grader for å måle denne vinkelen. Ved å tidligere bestemme torsjonskonstanten, blir den avstøtende kraften og verdien av ladningen som ervervet av hyllebærkulene enkelt beregnet.
Ingen har kommentert denne artikkelen ennå.