
Grashofs rettssaker, mekanismer, eksempler, applikasjoner
De Grashofs lov stater som: I en flat mekanisme med fire leddstenger med en av dem fast, kan minst en av stengene gjøre en hel sving, forutsatt at summen av den korteste stangen og den lengste stangen er mindre enn eller lik summen av de andre to.
Det er fem flate firestangs- eller koblingsmekanismer som overholder Grashofs lov (Et eksempel er vist i figur 1). For at stolpene eller koblingene til mekanismene som overholder loven skal gjøre en fullstendig sving, er det nødvendig at hver stolpe i en reell ordning opptar forskjellige parallelle plan.
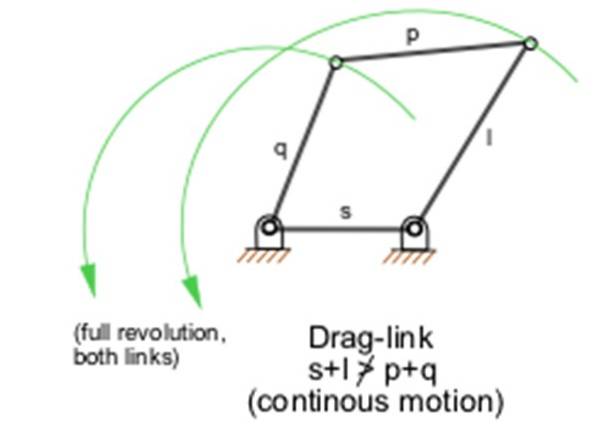
Grashofs lov er en enkel regel som lar deg designe en mekanisme som krever full rotasjon, enten fordi en motor vil være tilkoblet eller tvert imot fordi du vil transformere en oscillerende bevegelse til en roterende, på en slik måte at den er matematisk og fysisk levedyktig.
Artikkelindeks
- 1 Grensesaker
- 1.1 Typer av bevegelse
- 2 Mekanismer som er i samsvar med Grashofs lov
- 2.1 - Dobbel sveivmekanisme
- 2.2 - Flere mekanismer som overholder Grashofs lov
- 3 applikasjoner
- 3.1 Vev-vippemekanisme
- 3.2 Artikulert parallellogrammekanisme
- 3.3 Artikulert anti-parallellogrammekanisme
- 4 Referanser
Grensesaker
Anta at de fire leddstengene har følgende lengder ordnet fra minst til størst i henhold til:
s> p> q> l
Grashofs lov sier at for minst en bar eller lenke for å fullføre en revolusjon eller sving, må vilkåret være oppfylt:
s + l <= p + q
Denne ulikheten har følgende implikasjoner:
- Den eneste linjen eller lenken som kan gi full revolusjoner med hensyn til en annen er den korteste linjen.
- Hvis den kortere stangen går for fullt i forhold til en annen, vil den også gjøre full sving med hensyn til alle de andre.
Typer bevegelse
Bevegelsen av det leddede firsidene som overholder Grashofs lov kan være av følgende typer:
- Dobbel sving eller sveiv, hvis den korteste stangen er den faste, og de tilstøtende stengene gjør fullstendige svinger.
- Frem og tilbake, hvis den korte linjen ligger ved siden av den faste linjen.
- Dobbelt vippebryter, så lenge den korteste stangen er overfor den faste.
Når likheten er oppfylt i Grashof-formelen, er vi i det begrensende tilfellet der summen av den korteste linjen med den lengste linjen er lik summen av de to andre.
I dette tilfellet kan mekanismen ta en konfigurasjon der de fire stolpene er justert. Og det er i denne posisjonen, de ikke-faste skjøtene kan likegyldig gå den ene eller den andre, noe som får mekanismen til å låse seg..
Mekanismer som oppfyller Grashof-tilstanden er mer pålitelige og får mindre belastning på leddene og leddene, i den grad de er lenger fra det begrensende tilfellet av likhet.
Mekanismer som overholder Grashofs lov
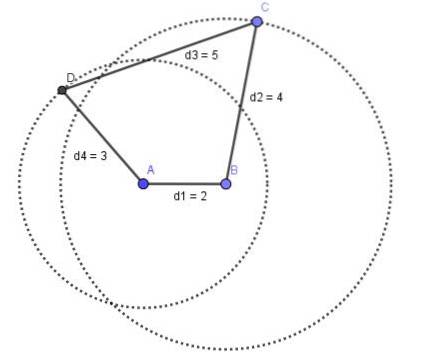
Vi vil betegne sammenhengende ledd med A, B, C og D, deretter:
- A og B er faste dreietaster.
- AB = d1 (fast stang)
- BC = d2
- CD = d3
- DA = d4
- Dobbel sveivmekanisme
Stolpene b2 og b4 roterer helt og Grashofs lov er oppfylt:
d1 + d3 <= d2+d4.
- Flere mekanismer som overholder Grashofs lov
Kjennetegnene til andre mekanismer som overholder Grashofs lov er nevnt og beskrevet nedenfor:
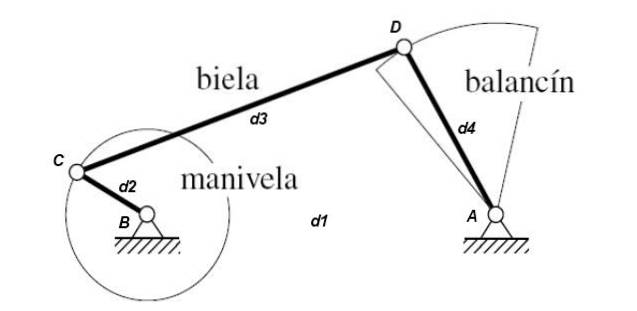
Veivmekanisme - vippe
D2 + d3 er oppfylt <= d1 + d4
Den kortere stangen d2 roterer helt og motsatt stang d4 gjør en vippebevegelse.
Dobbel vippemekanisme
- Den faste linjen AB er større enn motsatt CD og oppfyller at:
d1 + d3 <= d2 + d3
- For den kortere stangen (motsatt av den faste stangen), er den i stand til å gjøre en hel sving.
Leddet parallellogrammekanisme
- Stolpene AD og BC er like lange og alltid parallelle.
- På den annen side er stolpene AB og CD like lange og alltid parallelle.
- Når det gjelder motsatte stenger, har de samme lengde og d1 + d2 = d3 + d4 er oppfylt, ifølge Grashofs lov.
- Til slutt svinger stolpene AD og BC helt i samme retning.
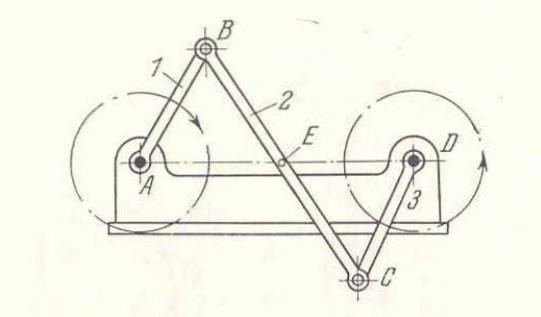
Artikulert antiparallelogram
- Stolpene AD og BC er like lange og ikke parallelle.
- For stenger AB og CD må de være like lange og ikke parallelle.
- På den annen side har motsatte stenger samme lengde, to av dem krysses.
- I denne mekanismen må følgende vilkår være oppfylt:
d1 + d2 = d3 + d4
- Rotasjonen av stolpene AD og BC er fullført, men i motsatt retning.
applikasjoner
Mekanismer som overholder Grashofs lov har flere anvendelser:
Veivmekanisme - Rocker
Den brukes på pedalsymaskinen, nyttig på de stedene der det ikke er strøm, der pedalen gjør en gyngende eller gyngende bevegelse, som overføres til et hjul som er forbundet med en remskive til symaskinen.
Et annet eksempel å nevne er vindusviskermekanismen. I dette er en motor koblet til veivstangen som utfører komplette svinger, og overfører en vippebevegelse til stangen som beveger systemets første børste..
En annen anvendelse av veiv-vippemekanismen er vippearmer for å pumpe olje fra bakken.

En motor er koblet til sveiven som roterer helt og overfører bevegelsen til pumpehodet eller vippearmen..
Leddet parallellogrammekanisme
Denne mekanismen pleide å brukes til å koble hjulene til damplokomotiver, slik at begge hjulene roterer i samme retning og med samme hastighet..
Hovedkarakteristikken for denne mekanismen er at stangen som forbinder begge hjulene har samme lengde som separasjonen av akslene..
Strømaftageren er et tegneinstrument som brukes til å kopiere og forstørre bilder. Den er basert på en firestangsmekanisme, der det er fire skjøter som danner toppunktene til et parallellogram..
Leddet anti-parallellogrammekanisme
Det er mekanismen som brukes i tennisballkastmaskinen, der hjulene som driver og lanserer ballen kreves for å rotere i motsatt retning..
Referanser
- Clemente C. Virtuelt laboratorium av en sveiv - vippemekanisme. Gradsarbeid i maskinteknikk. Universitetet i Almería. (2014). Gjenopprettet fra: repositorio.ual.es
- Hurtado F. Grashofs lov. Gjenopprettet fra: youtube.com
- Mech Designer. Kinematikk Grashof-kriterium. Gjenopprettet fra: mechdesigner.support.
- Shigley, J. Teori om maskiner og mekanismer. Mc-Graw Hill.
- Vi er F1. Fire-bar mekanismen analyse. Gjenopprettet fra: youtube.com
- UNAM. Utvikling av en firestangsmekanisme for bruk i undervisningen. Gjenopprettet fra: ptolomeo.unam.mx
- Wikipedia. Fire-bar kobling. Gjenopprettet fra: en.wikipedia.com
- Wikipedia. Grashofs lov. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.