
Ortogonale matriseegenskaper, bevis, eksempler

Den har en ortogonal matrise når nevnte matrise multiplisert med dens transponere resulterer i identitetsmatrisen. Hvis det inverse av en matrise er lik transponeringen, er den opprinnelige matrisen ortogonal.
Ortogonale matriser har den karakteristikken at antall rader er lik antall kolonner. Radvektorene er også ortogonale enhetsvektorer, og de transponerende radvektorene er også.
Når en ortogonal matrise multipliseres med vektorene i et vektorrom, produserer den en isometrisk transformasjon, altså en transformasjon som ikke endrer avstandene og bevarer vinklene.
En typisk representant for ortogonale matriser er rotasjonsmatriser. Transformasjonene av ortogonale matriser på et vektorrom kalles ortogonale transformasjoner.
De geometriske transformasjonene av rotasjon og refleksjon av punkter representert ved deres kartesiske vektorer utføres ved å påføre ortogonale matriser på de opprinnelige vektorene for å oppnå koordinatene til de transformerte vektorene. Det er av denne grunn at ortogonale matriser blir mye brukt i beregningsgrafisk prosessering..
Artikkelindeks
- 1 eiendommer
- 2 Demo
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 3.3 Eksempel 3
- 3.4 Eksempel 4
- 4 Referanser
Eiendommer
En matrise M er ortogonal hvis den multipliseres med dens transponering MT returnerer identitetsmatrisen Jeg. På samme måte resulterer produktet i transponering av en ortogonal matrise av den opprinnelige matrisen i identitetsmatrisen:
M MT = MT M = jeg
Som en konsekvens av forrige uttalelse har vi at transponering av en ortogonal matrise er lik dens inverse matrise:
MT = M-1.
Settet med dimensjonære ortogonale matriser n x n danner gruppen ortogonale O (n). Og delmengden av O (n) av ortogonale matriser med determinant +1 danner Gruppe av enhetlige spesialmatriser SU (n). Gruppematriser SU (n) er matriser som produserer lineære rotasjonstransformasjoner, også kjent som rotasjonsgruppe.
Demonstrasjon
La oss vise at en matrise er ortogonal hvis, og bare hvis radvektorene (eller kolonnevektorene) er ortogonale mot hverandre og av norm 1.
Anta at radene i en ortogonal matrise n x n er n ortonormale vektorer med dimensjonen n. Hvis betegnet med v1, vto,…., Vn n-vektorene er fornøyde:
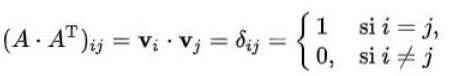
Hvor det er tydelig at settet med radvektorer er et sett med ortogonale vektorer med norm.
Eksempler
Eksempel 1
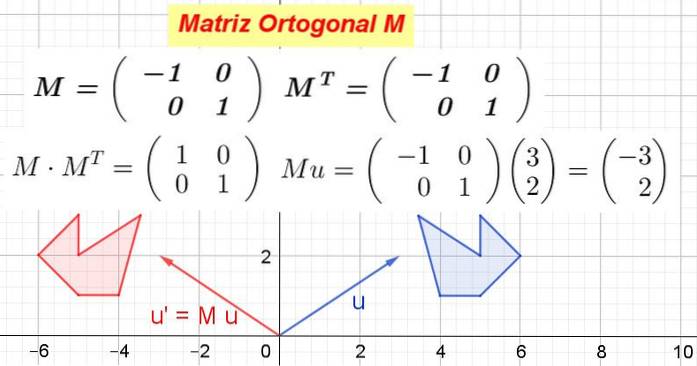
Vis at 2 x 2-matrisen som i første rad har vektoren v1= (-1 0) og i sin andre rad vektoren v2= (0 1) er en ortogonal matrise.
Løsning: Matrisen er bygget M og dens transponering beregnes MT:
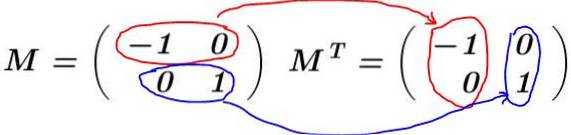
I dette eksemplet er matrisen M den er selvtransponert, det vil si at matrisen og dens transponering er identiske. Det multipliserer M ved å transponere MT:
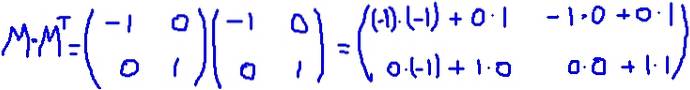
Det er bekreftet at M MT er lik identitetsmatrisen:
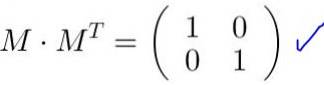
Når matrisen M multipliseres med koordinatene til en vektor eller et punkt, det oppnås nye koordinater som tilsvarer transformasjonen som matrisen lager på vektoren eller punktet.
Figur 1 viser hvordan M transformere vektor eller på eller' og også hvordan M forvandle den blå polygonen til den røde polygonen. Hva M er ortogonal det er da en ortogonal transformasjon, som bevarer avstandene og vinklene.
Eksempel 2
Anta at du har en 2 x 2 matrise definert i realene gitt av følgende uttrykk:
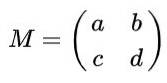
Finn de virkelige verdiene til til, b, c Y d slik at matrisen M være en ortogonal matrise.
Løsning: Per definisjon er en matrise ortogonal hvis den multipliseres med dens transponering, oppnås identitetsmatrisen. Husk at den transponerte matrisen er hentet fra originalen, og bytter rader mot kolonner, oppnås følgende likhet:
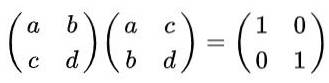
Gjennomføring av matrisemultiplikasjonen vi har:
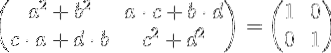
Ligning av elementene i venstre matrise med elementene i identitetsmatrisen til høyre, får vi et system med fire ligninger med fire ukjente a, b, c og d.
Vi foreslår følgende uttrykk for a, b, c og d når det gjelder trigonometriske forhold sinus og cosinus:
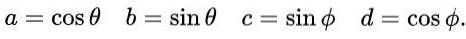
Med dette forslaget og på grunn av den grunnleggende trigonometriske identiteten, blir den første og tredje ligningen automatisk tilfredsstilt i likheten mellom matriseelementene. Den tredje og fjerde ligningen er den samme, og i matrixlikhet etter å ha erstattet de foreslåtte verdiene ser det slik ut:
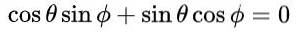
som fører til følgende løsning:
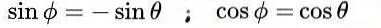
Til slutt oppnås følgende løsninger for den ortogonale matrisen M:
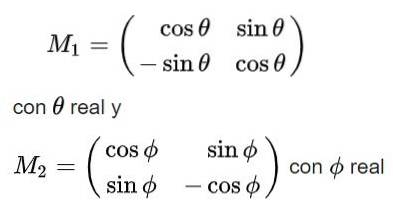
Merk at den første av løsningene har determinant +1 så den tilhører gruppen SU (2), mens den andre løsningen har determinant -1 og derfor ikke tilhører denne gruppen.
Eksempel 3
Gitt følgende matrise, finn verdiene til a og b slik at vi har en ortogonal matrise.
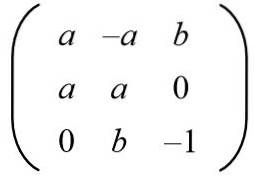
Løsning: For at en gitt matrise skal være ortogonal, må produktet med dens transponering være identitetsmatrisen. Deretter utføres matriksproduktet til den gitte matrisen med den transponerte matrisen, noe som gir følgende resultat:
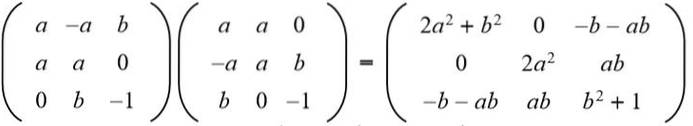
Deretter blir resultatet likestilt med 3 x 3 identitetsmatrisen:
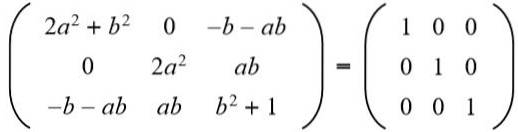
I andre rad tredje kolonne har vi (a b = 0), men til det kan ikke være null, for i så fall ville ikke likeverdigheten til elementene i andre rad og andre kolonne bli oppfylt. Da nødvendigvis b = 0. Erstatter b for verdien 0 vi har:
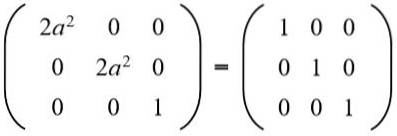
Deretter er ligningen løst: 2a ^ 2 = 1, hvis løsninger er: + ½√2 og -½√2.
Tar den positive løsningen for til følgende ortogonale matrise oppnås:
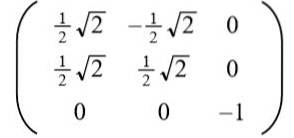
Leseren kan enkelt verifisere at radvektorene (og også kolonnevektorene) er ortogonale og enhetlige, det vil si ortonormale.
Eksempel 4
Bevis at matrisen TIL hvis radvektorer er v1 = (0, -1 0), v2 = (1, 0, 0) Y v3 = (0 0 -1) er en ortogonal matrise. Finn i tillegg hvordan vektorene til den kanoniske basen transformeres Jeg J K til vektorer u1, u2 Y u3.
Løsning: Det skal huskes at elementet (i, j) i en matrise multiplisert med dens transponering, er prikkproduktet til vektoren i rad (i) med kolonnen (j) i transponeringen. Videre er dette produktet lik Kronecker-deltaet i tilfelle matrisen er ortogonal:
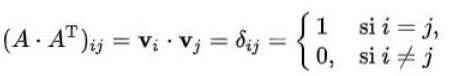
I vårt tilfelle ser det slik ut:
v1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1
v2 • v2 = 1 × 1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1
v1 • v2 = 0x1 + (-1) x0 + 0x0 = 0
v2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0
v2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0
v3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0
v1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0
v3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0
Som det er vist at det er en ortogonal matrise.
Hva mer u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) og til slutt u3 = A k = (0, 0, -1)
Referanser
- Anthony Nicolaides (1994) Determinants & Matrices. Bestå publikasjon.
- Birkhoff og MacLane. (1980). Modern Algebra, red. Vicens-Vives, Madrid.
- Casteleiro Villalba M. (2004) Introduksjon til lineær algebra. ESIC-redaksjon.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Students Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy press begrenset.
- Wikipedia. Ortogonal matrise. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Ortogonal matrise. Gjenopprettet fra: en.wikipedia.com



Ingen har kommentert denne artikkelen ennå.