De Bohr atommodell er den danske fysikeren Niels Bohr (1885-1962) sin oppfatning av atomets struktur, utgitt i 1913. I Bohr-atomet opptar elektronene rundt kjernen bare visse tillatte baner, takket være en begrensning som kalles kvantisering.
For Bohr var ikke bildet av atomet som et miniatyr solsystem, med elektroner som kretser rundt kjernen, ikke helt i samsvar med det faktum at elektriske ladninger, når de akselereres, utstråler energi..
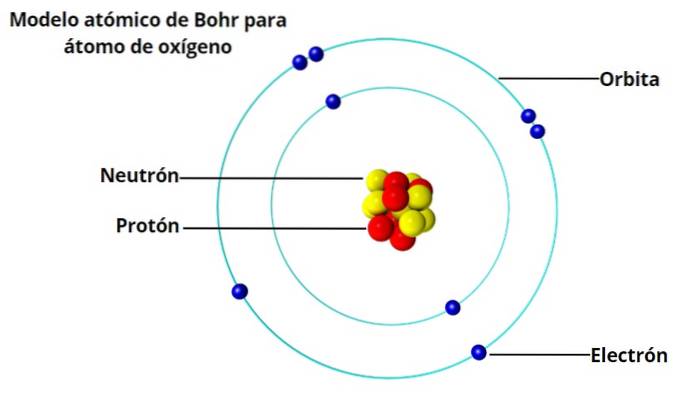
Et slikt atom ville ikke være stabilt, fordi det ville ende opp med å kollapse før eller senere fordi elektronene ville spiralere mot kjernen. Og da hadde de karakteristiske lysmønstrene som hydrogen og andre gasser avgir ved oppvarming, vært kjent i 50 år..
Mønsteret eller spekteret består av en serie lyse linjer med visse veldig spesifikke bølgelengder. Og hydrogenatomet kollapser ikke fra å avgi lys.
For å forklare hvorfor atomet er stabilt til tross for at det er i stand til å utstråle elektromagnetisk energi, foreslo Bohr at vinkelmoment bare kunne vedta visse verdier, og derfor også energi. Dette er hva som menes med kvantisering.
Ved å akseptere at energien ble kvantifisert, ville elektronen ha den nødvendige stabiliteten for ikke å skynde seg mot kjernen som ødelegger atomet..
Og atomet utstråler bare lysenergi når elektronen overgår fra en bane til en annen, alltid i diskrete mengder. På denne måten blir tilstedeværelsen av utslippsmønstre i hydrogen forklart..
Bohr komponerte således en visjon om atomet ved å integrere kjente konsepter fra klassisk mekanikk med nylig oppdagede, som Plancks konstant, fotonet, elektronet, atomkjernen (Rutherford hadde vært Bohrs mentor) og de nevnte problemspektrene..
Artikkelindeks
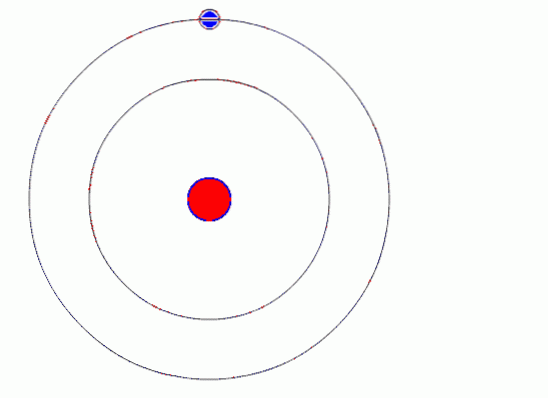
Bohrs atommodell antar at elektronen beveger seg i en sirkulær bane rundt kjernen ved virkningen av Coulombs elektrostatiske tiltrekningskraft og foreslår at elektronens vinkelmoment blir kvantifisert.
La oss se hvordan vi kan integrere begge begrepene i matematisk form:
La L være størrelsen på vinkelmomentet, m massen til elektronet, v elektronens hastighet og r baneens radius. For å beregne L har vi:
L = m⋅r⋅v
Bohr foreslo at L var lik heltallsmultipler av konstant h / 2π, hvor h er Planck er konstant, introdusert for kort tid siden av fysikeren Max Planck (1858-1947) da han løste problemet med energien som sendes ut av en svart kropp, en teoretisk gjenstand som absorberer alt innfallende lys.
Verdien er h = 6,626 × 10−34 J ・ s, mens en h / 2π er betegnet som ħ, det som leses "H bar".
Derfor forblir vinkelmomentet L:
m⋅r⋅v = nħ, med n = 1,2, 3 ...
Og fra denne tilstanden blir radiene til banene som er tillatt for elektronet utledet, som vi vil se nedenfor.
I det følgende vil vi anta det enkleste av atomene: hydrogen, som består av et enkelt proton og et elektron, begge med en ladning på størrelse e.
Den sentripetale kraften som holder elektronet i sin sirkulære bane, tilveiebringes av elektrostatisk tiltrekning, hvis størrelse F er:
F = keto/ rto
Hvor k er den elektrostatiske konstanten i Coulombs lov og r elektron-protonavstanden. Å vite at sentripetal akselerasjon i sirkelbevegelsec er gitt av forholdet mellom kvadratet av hastigheten og avstanden r:
tilc = vto / r
I følge Newtons andre lov er nettokraften produktet av massen m og akselerasjonen:
mvto/ r = keto/ rto
Forenkling av radius r får vi:
m⋅vtor = keto
Ved å kombinere dette uttrykket med vinkelmomentet har vi et ligningssystem gitt av:
1) mvtor = keto
2) r = n ħ/ mv
Tanken er å løse systemet og bestemme r, radiusen til den tillatte bane. Litt elementær algebra fører til svaret:
r = (nħ)to / k⋅m⋅eto
Med n = 1, 2, 3, 4, 5 ...
For n = 1 har vi den minste av radiene, kalt Bohr radius tileller med en verdi på 0,529 × 10−10 m. Radiene til de andre banene uttrykkes i form av tileller.
På denne måten introduserer Bohr det viktigste kvantetallet n, bemerker at de tillatte radiene er en funksjon av Plancks konstant, den elektrostatiske konstanten og massen og ladningen til elektronet.
Bohr kombinerer dyktig Newtons mekanikk med nye funn som kontinuerlig skjedde i andre halvdel av det nittende og begynnelsen av det tjuende århundre. Blant dem det revolusjonerende begrepet "kvante", som Planck selv hevdet ikke var veldig overbevist om.
Gjennom sin teori var Bohr i stand til å forklare seriene i hydrogenspekteret tilfredsstillende og forutsi energiutslipp i det ultrafiolette og infrarøde området, som ennå ikke hadde blitt observert..
Vi kan oppsummere postulatene slik:
Elektronen kretser rundt kjernen i en stabil sirkulær bane, med jevn sirkelbevegelse. Bevegelsen skyldes den elektrostatiske tiltrekningen som kjernen utøver på den.
Elektronens vinkelmoment blir kvantisert i henhold til uttrykket:
L = mvr = nħ
Der n er et helt tall: n = 1, 2, 3, 4 ..., noe som fører til at elektronet bare kan være i bestemte definerte baner, hvis radier er:
r = (n ħ)to / k m eto
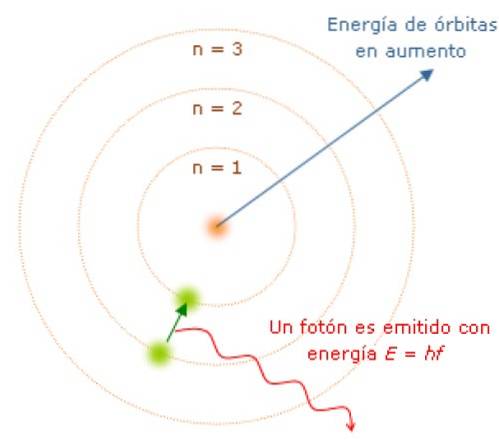
Siden vinkelmomentet er kvantifisert, er også energien E. Det kan vises at E er gitt av:
Elektron volt, eller eV, er en annen enhet for energi, mye brukt i atomfysikk. Det negative tegnet i energien sikrer banens stabilitet, noe som indikerer at det må gjøres arbeid for å skille elektronet fra denne posisjonen..
Mens elektronet er i sin bane, absorberer eller avgir det ikke lys. Men når den hopper fra en bane med høyere energi til en lavere, gjør den det..
Frekvensen f for det sendte lyset avhenger av forskjellen mellom energinivået i banene:
E = hf = Eførste - Eendelig
Bohr-modellen har visse begrensninger:
-Den brukes bare med hell på hydrogenatomet. Forsøk på å bruke den på mer komplekse atomer lyktes ikke.
-Det svarer ikke på hvorfor noen baner er stabile og andre ikke. Det faktum at energien i atomet ble kvantifisert fungerte veldig bra, men modellen ga ingen grunn, og det var noe som forårsaket forskere ubehag..
-En annen viktig begrensning er at den ikke forklarte tilleggslinjene som sendes ut av atomer i nærvær av elektromagnetiske felt (Zeeman-effekt og Stark-effekt). Eller hvorfor noen linjer i spekteret var mer intense enn andre.
-Bohr-modellen tar heller ikke hensyn til relativistiske effekter, som det er nødvendig å ta hensyn til, siden det ble eksperimentelt bestemt at elektroner er i stand til å nå hastigheter som er ganske nær lysets i vakuum..
-Det forutsetter at det er mulig å vite nøyaktig posisjonen og hastigheten til elektronet, men det som faktisk beregnes er sannsynligheten for at elektronet opptar en viss posisjon.
Til tross for sine begrensninger var modellen svært vellykket på den tiden, ikke bare for å integrere nye funn med allerede kjente elementer, men også fordi den reiste nye spørsmål, noe som gjorde det klart at veien til en tilfredsstillende forklaring av atomet lå i kvantemekanikken..
Schrödingers atommodell.
Atomic de Broglie-modellen.
Chadwick Atomic Model.
Heisenberg atommodell.
Perrins atommodell.
Thomsons atommodell.
Dalton atommodell.
Dirac Jordan atommodell.
Atomic model of Democritus.
Atomisk modell av Leucippus.
Sommerfeld atommodell.
Nåværende atommodell.
Ingen har kommentert denne artikkelen ennå.