
Pendelbevegelse
Hva er pendelbevegelsen?
De pendelbevegelse Det er en frem og tilbake bevegelse laget av en mer eller mindre tung gjenstand, kalt en pendel, suspendert av et tau eller en lysstang, festet i den andre enden.
Pendelen får en innledende impuls og får svinge, på denne måten beskriver objektet buer frem og tilbake. Dette er prinsippet om hvordan pendelklokker, svinger, gyngestoler og metronomer pendel, brukes til å markere tidene i musikk.
Det sies at rundt 1581 observerte Galileo Galilei oscillasjonen av en lampe i katedralen i Pisa, og observerte at selv om amplituden til kandelabers svingning avtok på grunn av friksjon med luften, ikke varigheten av lampesyklusen..
Dette fanget Galileo oppmerksomhet, som bestemte seg for å fortsette med studien og bestemte at pendelens periode ikke avhenger av massen, men av kvadratroten til akkordens lengde, som det vil bli vist senere..
Pendelbevegelsesegenskaper
En pendel er veldig enkel å bygge, siden det er nok med en loddrett som henger fra en bomullstråd og holdes i den andre enden med fingrene eller ved å feste den til en støtte som et spiker..
Etter den lille innledende impulsen er vekten ansvarlig for å holde pendelen svingende, selv om friksjonen reduserer bevegelsens amplitude, til den til slutt opphører helt..
Hovedkarakteristikken for pendelbevegelsen er å være repeterende, da det er en frem og tilbake bevegelse. Nå, for å lette studien, er det praktisk å gjøre noen forenklinger for å fokusere på en enklere modell, kalt enkel pendel.
Den enkle pendelen

Det er et ideelt system som består av en rørledning, betraktet som en punktmasse m, festet til et lett, uforlengbart tau med lengde L. Egenskapene til dette systemet er:
- Ha en repeterende og periodisk bevegelse, bestående av å gå frem og tilbake en bue med radius omkrets lik L.
- Tar ikke hensyn til friksjon.
- Bevegelsesområdet er lite (< 5º).
- Perioden er uavhengig av massen m, og avhenger bare av lengden L pendel.
Formler og ligninger
Følgende er et diagram over den enkle pendelen, som to krefter virker på: vekten P av størrelsesorden mg, som er rettet vertikalt nedover og spenningen T På tauet. Friksjon blir ikke vurdert.
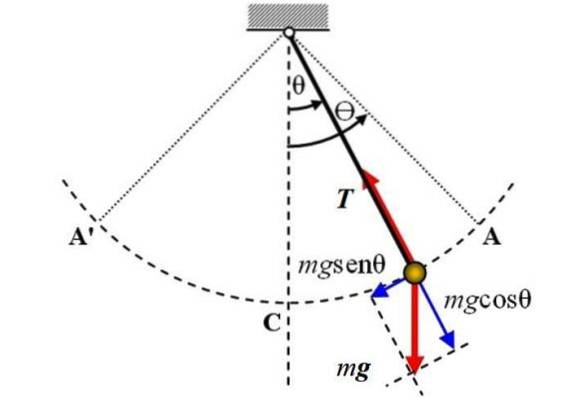
Referanseaksen er den vertikale aksen og sammenfaller med posisjonen θ = 0, derfra måles vinkelforskyvningen θ, enten i en eller annen retning. + Tegnet kan tilordnes til høyre skift i figuren.
For å studere pendelens bevegelse velges et koordinatsystem med opprinnelsen ved selve pendelen. Dette systemet har en tangentiell koordinat til omkretsbuen A'CA beskrevet av pendelen, samt en radiell koordinat, rettet mot sentrum av banen..
I øyeblikket vist i figuren beveger pendelen seg til høyre, men den tangensielle komponenten av tyngdekraften, kalt Ft, er ansvarlig for å få ham tilbake. Det kan ses av figuren at denne komponenten har motsatt retning av bevegelse.
Når det gjelder spenningen i tauet, er det balansert med komponenten av vekten mgcosθ.

Vinkelforskyvning
Vi må uttrykke ligningen i form av en enkelt variabel, og huske at vinkelforskyvningen θ og den buede buen er relatert av ligningen:
s = L.θ
Massen avbrytes på begge sider, og hvis amplituden er liten, vil vinkelen θ også, så følgende tilnærming er gyldig:
sen θ ≈ θ
Med dette oppnås følgende differensialligning for variabelen θ (t):


Denne ligningen er veldig enkel å løse, siden løsningen er en funksjon hvis andre derivat er selve funksjonen. Det er tre alternativer: et cosinus, en sinus eller en eksponentiell. Cosinusfunksjonen er valgt for vinkelforskyvningen θ (t), siden den er en velkjent og brukervennlig funksjon.
Leseren kan verifisere, ved å skille to ganger, at følgende funksjon tilfredsstiller differensiallikningen:
θ (t) = θm cos (ωt + φ)
Hvor θm er den maksimale vinkelen som pendelen beveger seg i forhold til vertikal og vinkelfrekvensen ω er:

Periodens ligning
Perioden T for bevegelsen er tiden det tar å utføre en syklus og er definert som:

Erstatter ω:

Som nevnt ovenfor avhenger ikke perioden av pendelens masse, men bare av lengden..
Eksempler på pendelbevegelse
Pulsmåling
Galileo hadde ideen om å måle hjerterytmen til mennesker, justere lengden på pendelen for å få perioden til å falle sammen med hjerterytmen til en person.
Pendelklokken
Dette er utvilsomt et av de mest kjente eksemplene på pendelbevegelse. Å lage pendelklokke handler like mye om vitenskap som om kunst. Den nederlandske fysikeren Christian Huygens (1629-1695) utviklet den første pendelklokken i 1656, basert på studien utført av Galileo for mange år siden..
Foucaults pendel

Det er en noe annen pendel enn den som er beskrevet ovenfor, siden den er i stand til å rotere i et hvilket som helst vertikalt plan. Den ble opprettet av den franske fysikeren Léon Foucault (1819-1868) og brukes til å visualisere jordens rotasjon.
Treningen løst
En enkel pendel passerer hvert 0,5 s gjennom likevektsposisjonen. Hva er lengden på tråden?
Løsning
Siden perioden er tiden det tar å fullføre en komplett syklus, der den går gjennom likevektsposisjonen to ganger: den ene går og den andre tilbake, deretter:
T = 2 × 0,5 s = 1 s
Fra:

Lengden L på tråden er ryddet:

Tråden er 0,25 m eller 25 cm lang.
Referanser
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 2. Dynamikk. Redigert av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysikk. 2. plass. Ed. McGraw Hill.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
- Katz, D. 2013. Fysikk for forskere og ingeniører. Fundamenter og forbindelser. Cengage læring.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.



Ingen har kommentert denne artikkelen ennå.