Relativ bevegelse i en dimensjon, i to dimensjoner, øvelser

De relativ bevegelse av en partikkel eller en gjenstand er den som observeres med hensyn til et bestemt referansepunkt som observatøren har valgt, som kan være fast eller i bevegelse. Hastighet refererer alltid til noe koordinatsystem som brukes til å beskrive det.

For eksempel er passasjeren til en bil i bevegelse og som sover komfortabelt i setet i ro i forhold til sjåføren, men ikke for en observatør som står på fortauet og ser bilen gå forbi..

Da er bevegelsen alltid relativ, men det hender at koordinat- eller referansesystemet generelt velges med opprinnelse i jorden eller bakken, et sted som anses som stasjonært. På denne måten er bekymringen fokusert på å beskrive bevegelsen til objektet som studeres..

Er det mulig å beskrive hastigheten på den sovende copiloten sammenlignet med en passasjer som reiser i en annen bil? Svaret er ja. Det er frihet til å velge verdien av (x_eller, Y_eller, z_eller): opprinnelsen til referansesystemet. Valget er vilkårlig og avhenger av observatørens preferanse, samt hvor enkelt det er å løse problemet..

Artikkelindeks

• 1 Relativ bevegelse i en dimensjon
  • 1.1 - Arbeidet eksempel 1
• 2 Relativ bevegelse i to og tre dimensjoner
  • 2.1 -Løst øvelse 2 
  • 2.2 -Løst øvelse 3
• 3 Referanser

Relativ bevegelse i en dimensjon

Når bevegelsen skjer langs en rett linje, har mobilene hastigheter i samme retning eller i motsatt retning, begge sett av en observatør som står på jorden (T). Flytter observatøren seg med hensyn til mobilene? Ja, med samme hastighet som de har, men i motsatt retning.

Hvordan beveger den ene mobilen seg i forhold til den andre? For å finne ut av blir hastighetene lagt til vektorielt.

-Arbeidet eksempel 1

Henvis til figuren som vises, angi den relative hastigheten til bil 1 i forhold til bil 2 i hver situasjon.

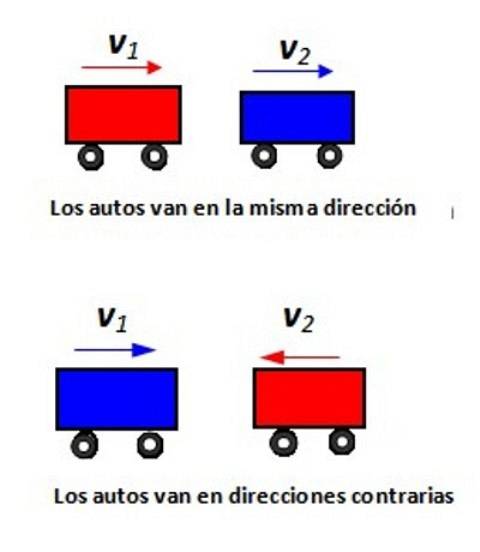
Løsning

Vi vil tildele et positivt tegn til hastighetene til høyre og et negativt tegn til venstre. Hvis en mobil går til høyre i 80 km / t, ser en passasjer på denne mobilen observatøren på jorden bevege seg i - 80 km / t.

Anta at alt skjer langs x-aksen. I den følgende figuren beveger den røde bilen seg i +100 km / t (sett fra T) og er i ferd med å passere den blå bilen som kjører i +80 km / t (sett også fra T). Hvor raskt nærmer en passasjer i den blå bilen seg til den røde bilen?

Etikettene er: v _1/2 hastighet på bil 1 i forhold til bil 2, v_{1 / T} bilens hastighet med hensyn til T, v_{T / 2} hastighet av T med hensyn til 2. Vektortilsetning:

v_1/2 = v_{1 / T} + v_{T / 2} = (+100 km / t - 80 km / t) x= 20 km / t x

Vi kan klare oss uten vektornotasjonen. Legg merke til abonnementene: Hvis du multipliserer de to til høyre, bør du få den til venstre.

Og når de går den andre veien? Nå v_{1 / T} = + 80 km / t og v_{2 / T} = -100 km / t, derfor v_{T / 2} = + 100 km / t. Passasjeren til den blå bilen vil se den røde bilen nærme seg:

v_{1/2 =} v_{1 / T} + v_{T / 2} = +80 km / t +100 km / t = 180 km / t

Relativ bevegelse i to og tre dimensjoner

I følgende ordning, r er flyets posisjon sett fra systemet X og Z, rer posisjonen fra systemet X og Z ' Y R er systemets posisjon med en premie i forhold til systemet uten premie. De tre vektorene danner en trekant der R + r'= r, Og dermed r'= r - R.

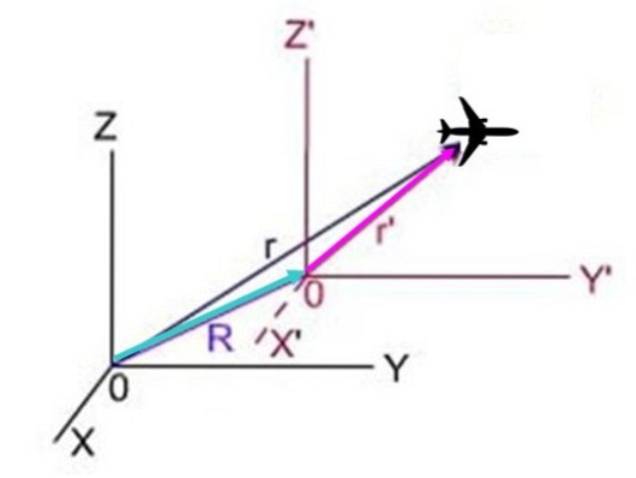
Siden derivatet med hensyn til posisjonstid er nøyaktig hastigheten, resulterer det:

v'= v - eller

I denne ligningen v'er flyets hastighet i forhold til systemet X og Z ', v er hastigheten i forhold til systemet X og Z Y eller er den primære systemets konstante hastighet med hensyn til det ikke-primede systemet.

-Trening løst 2 

Et fly er på vei nordover med flyhastighet på 240 km / t. Plutselig begynner vinden å blåse fra vest til øst med en hastighet på 120 km / avhengig av jorden.

Finn: a) Hastigheten til flyet i forhold til bakken, b) Avviket som piloten opplever c) Korreksjonen som piloten må gjøre for å kunne sikte direkte nordover og den nye hastigheten i forhold til bakken, en gang korreksjonen er gjort.

Løsning

a) Det er følgende elementer: plan (A), bakken (T) og vind (V).

I koordinatsystemet der nord er + y-retningen og vest-øst-retningen er + x, har vi de oppgitte hastighetene og deres respektive etikett (abonnement):

v _AV = 240 km / t (+Y); v _{V / T} = 120 km / t (+x); v _{A / T} = ?

Den riktige vektorsummen er:

v _{A / T} = v _AV + v _{V / T} = 240 km / t (+Y) + 120 km / t (+x)

Størrelsen på denne vektoren er: v _{A / T} = (240 ^to+ 120^to)^1/2 km / t = 268,3 km / t

b) θ = arctg (v _AV / v _{V / T}) = arctg (240/120) = 63,4 º Nord for Øst eller 26,6 º Nordøst.

c) For å fortsette nordover med denne vinden, må du peke flyets bue mot nordvest, slik at vinden skyver deg direkte mot nord. I dette tilfellet vil flyets hastighet sett fra bakken være i + y-retningen, mens hastigheten på flyet i forhold til vinden vil være nordvest (det trenger ikke nødvendigvis å være 26,6º).

Av Pythagoras teorem:

v _{A / T} = (240 ^to- 120^to)^1/2 km / t = 207,8 km / t

α = arctg (v _{V / T} / v _{A / T} ) = arctg (120 / 207.8) = 30º nordvest

-Trening løst 3

Det tar en person to minutter å gå ned en stasjonær rulletrapp. Hvis stigen fungerer, tar det personen 1 minutt å gå ned mens han står stille. Hvor lang tid tar det for personen å gå ned med stigen i gang?

Løsning

Det er tre elementer å vurdere: personen (P), stigen (E) og bakken (S), hvis relative hastigheter er:

v_{P / E} : personens hastighet med hensyn til stigen; v_{DET ER}: stigens hastighet i forhold til bakken; v_{P / S}: personens hastighet i forhold til bakken.

Som sett fra bakken av en fast observatør, har personen som stiger ned stigen (E) en hastighet v _{P / S} gitt av:

v _{P / S} = v_{P / E} + v_{DET ER}

Den positive retningen er å gå ned stigen. Være t  tiden det tar å gå ned og L avstand. Størrelsen på personens hastighet v _{P / S} Det er:

v_{P / S} = L / t

t₁ er tiden det tar å gå ned med stigen stoppet: v _{P / E} = L / t₁

Og T_to den som tar deg stille ned på trappen i bevegelse: v _{DET ER} = L / t_to

Kombinere uttrykkene:

L / t = L / t₁ + L / t_to

Erstatte numeriske verdier og løsning t:

1 / t = 1 / t₁ + 1 / t_to = 1/2 + 1/1 = 1,5

Så t = 1 / 1,5 minutter = 40 sekunder.

Referanser

1. Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Volum 3. Utgave. Kinematikk. 199-232.
3. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. 6^th. Ed. Prentice Hall. 62-64.
4. Relativ bevegelse. Gjenopprettet fra: courses.lumenlearning.com
5. Wilson, J. 2011. Fysikk 10. Pearson Education. 166-168.