Vinkler i omkretsstyper, egenskaper, løste øvelser

Kalt omkretsvinkler de der noen av elementene er eller krysser hverandre ved en gitt omkrets. Blant dem er følgende:

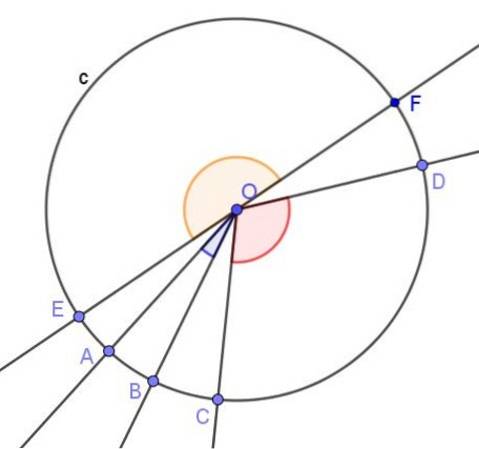
1.- The sentral vinkel, hvis toppunkt er i midten av omkretsen og dets sider er sekant for den, som vi ser på følgende bilde:

2.- The innskrevet vinkel, hvis toppunkt er på omkretsen og dens sider er sekant eller tangent til omkretsen.

3.- Utenfor vinkel, hvis toppunkt er utenfor omkretsen, men sidene er sekant eller tangent til omkretsen.

4.- The innvendig vinkel, med toppunktet inne i omkretsen og sidene er skille til det.

Alle disse vinklene har visse forhold til hverandre, og dette fører oss til viktige egenskaper mellom vinklene som tilhører en gitt sirkel.

Artikkelindeks

• 1 eiendommer
  • 1.1 - Sentral vinkel
  • 1.2 - Innskrevet vinkel
  • 1.3 - Utvendig vinkel
  • 1.4 - Innvendig vinkel
• 2 Løst øvelser
  • 2.1 - Øvelse 1
  • 2.2 - Øvelse 2
• 3 Referanser

Eiendommer

- Sentral vinkel

Den sentrale vinkelen er definert som den som har toppunktet i sentrum av omkretsen og dens sider krysser omkretsen.

Tiltaket i radianer av en sentral vinkel er kvotienten mellom den underliggende buen, det vil si omkretsbuen mellom sidene av vinkelen og radiusen av omkretsen. 

Hvis omkretsen er enhetlig, det vil si av radius 1, er målet på den sentrale vinkelen lengden på buen, som tilsvarer antall radianer.

Hvis du vil måle den sentrale vinkelen i grader, multipliserer du målingen i radianer med faktoren 180º / π.

Vinkelmåleinstrumenter, som for eksempel vinkelmåler og goniometer, bruker alltid en sentral vinkel og lengden på den subtente buen.

De er kalibrert i seksagesimale grader, noe som betyr at når en vinkel måles med dem, i bakgrunnen er det som måles lengden på buen som er undertrykket av den sentrale vinkelen.

Eiendom

Tiltaket for en sentral vinkel i radianer er lik lengden på den nedadgående eller avlyttende buen delt på lengden på radiusen.

- Innskrevet vinkel

Den innskrevne vinkelen til en sirkel er en som har toppunktet på omkretsen og dens stråler er sekant eller tangent til den.. 

Dens egenskaper er:

Eiendommer

-Den innskrevne vinkelen er konveks eller plan.

-Når en innskrevet vinkel krysser samme bue som den sentrale vinkelen, vil målet på den første vinkelen være halvparten av den andre..

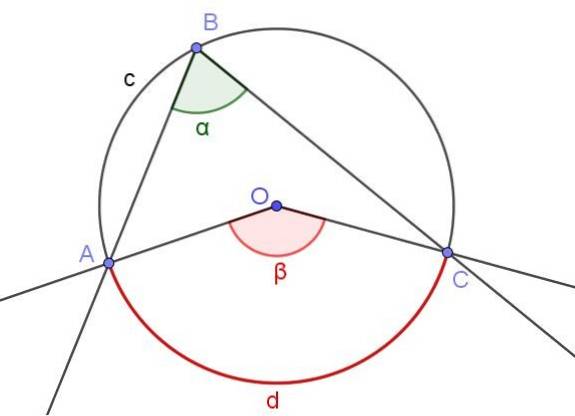
Figur 3 viser to vinkler ∠ABC og ∠AOC som krysser samme omkretsbue A⌒C.

Hvis målingen på den innskrevne vinkelen er α, er målingen β av den sentrale vinkelen dobbelt så stor som målingen for den innskrevne vinkelen (β = 2 α) fordi begge understreker den samme målebuen d.

- Utenfor vinkel

Det er vinkelen hvis toppunkt er utenfor omkretsen, og hver av sidene kutter omkretsen på ett eller flere punkter.

Eiendom

-Målene er lik halvforskjellen (eller forskjellen delt på 2) av de sentrale vinklene som fanger opp de samme buene.

For å sikre at målingen er positiv, må semiforskjellen alltid være den for den største sentrale vinkelen minus tiltaket for den minste sentrale vinkelen, som illustrert i følgende figur.

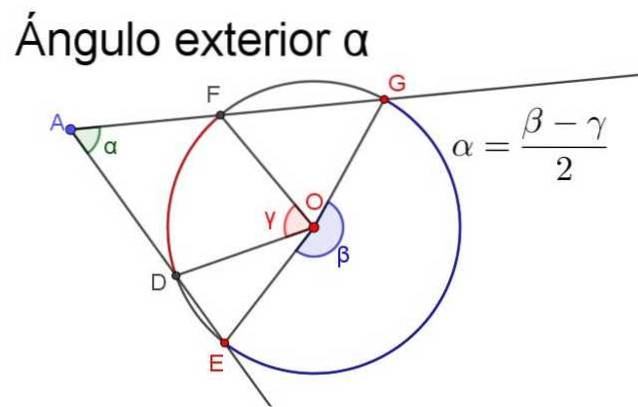
- Indre vinkel

Den indre vinkelen er den som har toppunktet inne i omkretsen, og sidene krysser omkretsen.

Eiendom 

Målene er lik halvsummen av den sentrale vinkelen som understreker den samme buen, pluss den sentrale vinkelen som legger den samme buen som forlengelsesvinkelen (dette er den indre vinkelen som dannes av strålene som er komplementære til den opprinnelige innvendige vinkelen ).

Følgende figur illustrerer og klargjør egenskapen til den innvendige vinkelen.

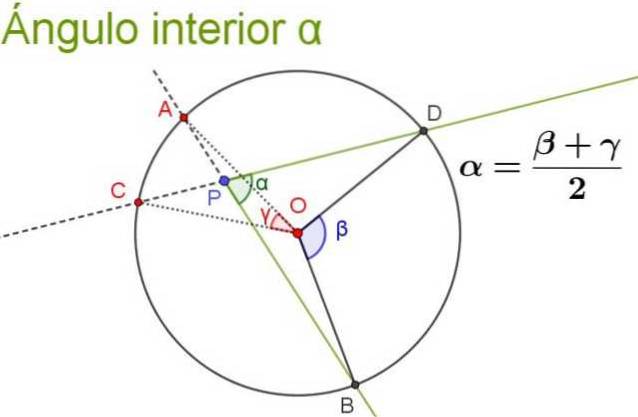
Løst øvelser

- Øvelse 1

Anta en innskrevet vinkel der en av sidene passerer gjennom sentrum av sirkelen, som vist i figur 6. Radien til sirkelen er OA = 3 cm og buen d har en lengde på π / 2 cm. Bestem verdien av vinklene α og β.

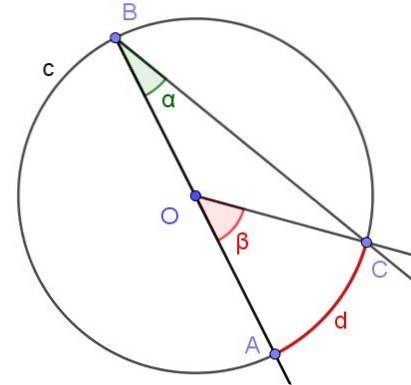
Løsning

I dette tilfellet dannes den likebenede trekanten COB, siden [OC] = [OB]. I en likeverdig trekant er vinklene ved siden av basen like, derfor ∠BCO = ∠ABC = α. På den annen side ∠COB = 180º - β. Tatt i betraktning summen av de indre vinklene til trekanten COB, har vi:

α + α + (180 º - β) = 180 º

Fra hvilket det følger at 2 α = β, eller hva som er ekvivalent α = β / 2, som egenskapen (3) i forrige avsnitt er bekreftet med, at målingen på den innskrevne vinkelen er halvparten av den sentrale vinkelen, når begge vinkler undertrykke samme akkord [AC].

Nå fortsetter vi med å bestemme de numeriske verdiene: vinkelen β er sentral og dens mål i radianer er kvotienten mellom buen d og radiusen r = OA, så dens mål er:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30 º.

På den annen side hadde det allerede blitt uttalt at α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Øvelse 2

I figur 7 er vinklene α₁ og β_to de har samme mål. Videre vinkelen β₁ måler 60º. Bestem vinklene β og α.

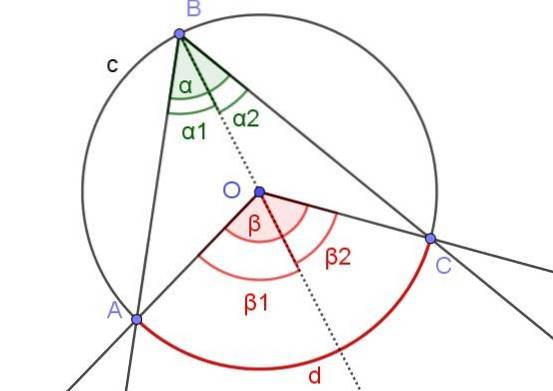
Løsning

I dette tilfellet har vi en innskrevet vinkel ∠ABC der sentrum O av omkretsen er innenfor vinkelen.

På grunn av egenskapen (3) har vi α_to = β_to / 2 og α₁ = β₁ /to. Hva:

α = α₁ + α_to og β = β₁ + β_to

Derfor følger det at:

α = α₁ + α_to = β₁ / 2 + β_to / 2 = (β₁ + β_to) / 2 = β / 2.

I følge egenskapene:

α = β / 2

Siden vi blir fortalt at β₁ = 60º da:

α₁ = β₁ / 2 = 60º / 2 = 30º.

De forteller oss også at α₁ = β_to så det følger at:

β_to = 30º.

Vinkelen β resulterer:

β₁ + β_to = 60º + 30º = 90º.

Og siden α = β / 2, da:

α = 90º / 2 = 45º. 

For å konkludere:

β = 90º og α = 45º.

Referanser

1. Baldor, A. 1973. Geometri og trigonometri. Mellomamerikansk kulturforlag.
2. E. A. 2003. Elementer av geometri: med øvelser og kompassgeometri. University of Medellin.
3. Geometri 1. ESO. Vinkler på omkretsen. Gjenopprettet fra: edu.xunta.es.
4. All vitenskap. Løste problemer med vinkler i omkretsen. Gjenopprettet fra: francesphysics.blogspot.com
5. Wikipedia. Innskrevet vinkel. Gjenopprettet fra: es.wikipedia.com