
Vinkler motsatt av vertexen (med øvelse løst)
De Motsatte vinkler ved toppunktet er de som oppfyller følgende: sidene til en av dem er forlengelsene av sidene til den andre vinkelen. De grunnleggende setning av vinklene motsatt av toppunktet sier slik: to vinkler motsatt av toppunktet har samme mål.
Språk blir ofte misbrukt ved å si at vinklene overfor toppunktet er like, noe som ikke er riktig. Bare fordi to vinkler har samme mål, betyr ikke det at de er like. Det er som å si at to barn som er i samme høyde er like.
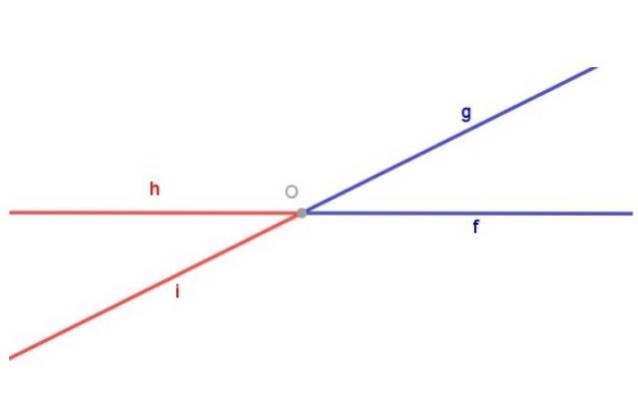
Husk at en vinkel er definert som den geometriske figuren som består av to stråler med samme opprinnelse.
Figur 1 viser vinkelen tåke (blå) sammensatt av strålen [Av) og strålen [Og) av vanlig opprinnelse ELLER. Figur 1 viser også vinkelen hoi (rød) sammensatt av strålen [Jeg hørte) og strålen [Åh) begge med opprinnelse ELLER.
To vinkler motsatt av toppunktet er to forskjellige geometriske figurer. For å markere dette, er vinkelen farget i figur 1 tåke blå, mens vinkelen hoi har blitt farget rødt.
De blå og røde vinklene i figur 1 er motsatte i toppunktet fordi: strålen [Av) av den blå vinkelen er forlengelsen av strålen [Åh) av den røde vinkelen og strålen [Og) av den blå vinkelen er forlengelsen av strålen [Jeg hørte) av den røde vinkelen.
Artikkelindeks
- 1 Viktige begreper om vinkler
- 1.1 Sider og hjørner av en vinkel
- 1.2 Vinkler dannet av to kryssende linjer
- 2 Vinkelrette linjer og rett vinkel
- 2.1 Stråler på samme linje og plan vinkel
- 2.2 Nullvinkel og full vinkel
- 3 Vinkelmåling
- 3.1 Sexagesimalt system
- 4 Vertex Angles Theorem
- 4.1 Demo
- 5 Øvelse løst
- 5.1 Løsning
- 6 Referanser
Viktige konsepter om vinkler
Sider og hjørner av en vinkel
Den geometriske figuren som består av to stråler med felles opprinnelse er en vinkel. Følgende bilde viser vinkelen POQ dannet av de to strålene [OP) Y [OQ] av vanlig opprinnelse ELLER:
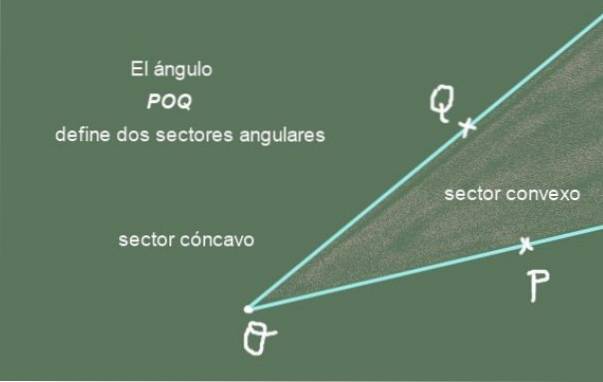
Strålene [OP) Y [OQ] er vinkelsider POQ, mens det felles punktet O kalles vinkel toppunkt.
Vinkelsektor: En vinkel deler planet som inneholder det i to vinkelsektorer. En av dem er den konvekse vinkelsektoren og den andre er den konkave vinkelsektoren. Foreningen av de to sektorene gir hele planet.
Figur 2 viser vinkelen POQ og de to vinkelsektorene. Den konvekse vinkelsektoren er den med spiss form, mens den konkave er vinkelsektoren til planet som mangler den konvekse sektoren.
Vinkler dannet av to linjer som krysser hverandre
To kryssende linjer i et plan danner fire vinkler og deler planet i fire vinkelsektorer.
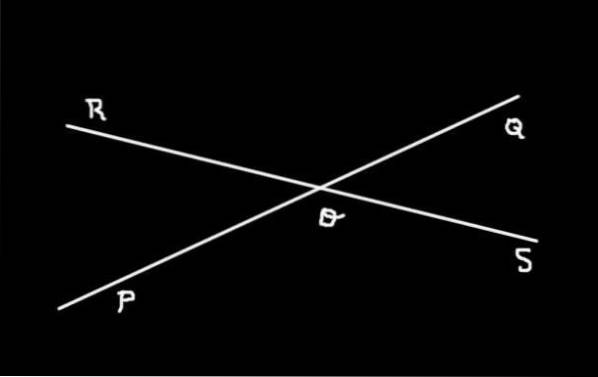
Figur 3 viser de to linjene (PQ) Y (RS) som blir fanget opp i ELLER. Der kan man se at fire vinkler bestemmes:
-SOQ, QOR, ROP Y POS
Vinklene SOQ Y QOR, QOR Y ROP, ROP Y POS, POS Y SOQ De er tilstøtende vinkler hverandre, mens SOQ Y ROP de er motsatt i toppunktet. De er også Motsatte vinkler ved toppunktet Vinklene QOR Y POS.
Vinkelrette linjer og rette vinkler
To secant linjer (kryssende linjer) er Vinkelrette rette linjer hvis de bestemmer fire vinkelsektorer med like mål. Hvis hver av de fire sektorene er symmetriske med den tilstøtende vinkelsektoren, har de samme mål.
Hver av vinklene som bestemmer de to vinkelrette linjene kalles rett vinkel. Alle rette vinkler har samme mål.
Stråler på samme linje og plan vinkel
Gitt en linje og et punkt på den, er to stråler definert. Disse to strålene definerer to plane vinkler.
I figur 3 kan du se linjen (RS) og poenget ELLER som tilhører (RS). Vinkelen SOR er en plan vinkel. Det kan også anføres at vinkelen ROS er en plan vinkel. Alle planvinkler har samme mål.
Null vinkel og full vinkel
En enkelt stråle definerer to vinkler: en av dem er den for den konvekse vinkelsektoren null vinkel og den andre, den konkave vinkelsektoren er full vinkel. I figur 3 kan du se null vinkel SOS og full vinkel SOS.
Vinkelmåling
Det er to tallsystemer som ofte brukes til å gi mål på en vinkel.
En av dem er det seksagesimale systemet, det vil si basert på tallet 60. Det er en arv fra de gamle mesopotamiske kulturene. Det andre systemet for vinkelmåling er radiansystemet, basert på tallet π (pi) og er et arv fra de gamle greske vismennene som utviklet geometri.
Sexagesimal system
Null vinkel: i sexagesimal-systemet måler nullvinkelen 0º (null grader).
Full vinkel: det tildeles tiltaket 360º (tre hundre og seksti grader).
Planvinkel: i sexagesimal-systemet måler vinkelen 180 ° (hundre og åtti grader).
Rett vinkel: to vinkelrette linjer deler planet i fire like vinkler, kalt rette vinkler. Mål på rett vinkel er den fjerde delen av den komplette vinkelen, det vil si 90 ° (nitti grader).
Vinkelmåler eller goniometer
Vinkelmåleren er instrumentet som brukes til å måle vinkler. Den består av en halvcirkel (vanligvis klar plast) delt inn i 180 vinklede seksjoner. Siden en halvcirkel danner en plan vinkel, er målet mellom to påfølgende seksjoner 1º.
Goniometeret ligner vinkelmåler og består av en sirkel delt inn i 360 vinkelsnitt.
En vinkel der sidene starter fra midten av goniometeret, krysser to sektorer, og målene for denne vinkelen i grader er lik antall n snitt mellom de to skjæringssektorene, i dette tilfellet vil målet være nº (det står "Jan grader”).
Vertex Angels Theorem
Formelt settes setningen slik:
Hvis to vinkler er loddrett motsatt, har de samme mål.
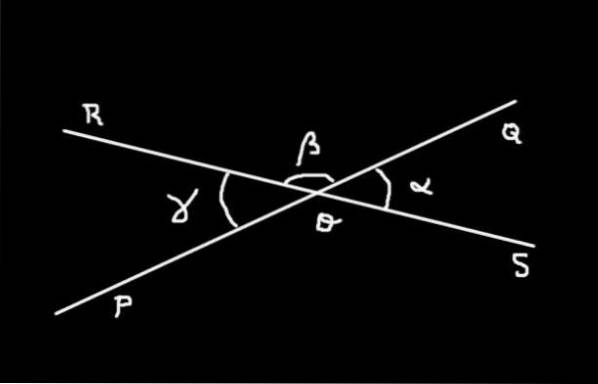
Demonstrasjon
Vinkelen SOQ har mål α; vinkelen QOR har mål β og vinkel ROP har mål γ. Summen av vinkelen SOQ mer ham QOR danner planvinkelen SOR måler 180º.
Det er:
α + β = 180º
På den annen side og bruker samme resonnement med vinklene QOR Y ROP du har:
β + γ = 180º
Hvis vi observerer de to foregående ligningene, er den eneste måten at begge oppfylles, at α er lik γ.
Hva SOQ har mål α og er motsatt av toppunktet til ROP av mål γ, og siden α = γ, konkluderes det med at vinklene motsatt toppunktet har samme mål.
Treningen løst
Med henvisning til figur 4: Anta at β = 2 α. Finn mål på vinklene SOQ, QOR Y ROP i seksagesimale grader.
Løsning
Som summen av vinkelen SOQ mer ham QOR danner planvinkelen SOR du har:
α + β = 180º
Men de forteller oss at β = 2 α. Ved å erstatte denne verdien av β har vi:
α + 2 α = 180º
Nemlig:
3 α = 180º
Noe som betyr at α er den tredje delen av 180º:
α = (180º / 3) = 60º
Så måler du SOQ er α = 60º. Mål på QOR er β = 2 α = 2 * 60º = 120º. Endelig som ROP er motsatt av toppunkt til SOQ så ifølge den allerede bevist setning har de samme mål. Det vil si målet på ROP er γ = α = 60º.
Referanser
- Baldor, J. A. 1973. Plane and Space Geometry. Mellomamerikansk kultur.
- Matematiske lover og formler. Vinkelmålesystemer. Gjenopprettet fra: ingemecanica.com.
- Wikipedia. Motsatte vinkler ved toppunktet. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Transportør. Gjenopprettet fra: es.wikipedia.com
- Zapata F. Goniómetro: historie, deler, drift. Gjenopprettet fra: lifeder.com



Ingen har kommentert denne artikkelen ennå.