
Imaginære tallegenskaper, applikasjoner, eksempler
De imaginære tall er de som gir en løsning på ligningen der det ukjente, kvadrat, er lik et negativt reelt tall. Den imaginære enheten er i = √ (-1).
I ligningen: zto= - a, z er et imaginært tall som uttrykkes som følger:
z = √ (-a) = i√ (a)
Å være til et positivt reelt tall. Ja a = 1, deretter z = i, hvor Jeg er den tenkte enheten.
Generelt sett uttrykkes et rent imaginært tall z alltid i form:
z = y⋅i
Hvor Y er et reelt tall e Jeg er den tenkte enheten.
Akkurat som reelle tall er representert på en linje, kalt ekte rett, på en analog måte er de imaginære tallene representert på imaginær linje.
De imaginær linje er alltid vinkelrett (90 ° form) til ekte rett og de to linjene definerer et kartesisk plan kalt komplekst plan.
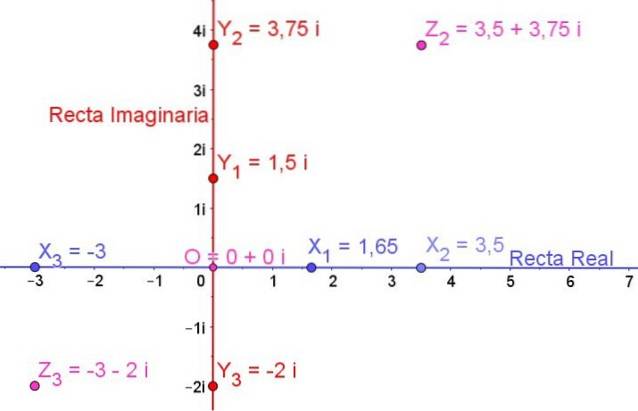
I figur 1 vises det komplekse planet, og på det er noen reelle tall representert, noen imaginære tall og også noen komplekse tall:
X1, Xto, X3 de er reelle tall
Y1, Yto, Y3 de er imaginære tall
Zto og Z3 de er komplekse tall
Tallet O er det virkelige null og det er også det imaginære null, så opprinnelsen O er det komplekse null uttrykt med:
0 + 0i
Artikkelindeks
- 1 eiendommer
- 1.1 Addisjon og subtraksjon av imaginær
- 1.2 Produkt av forestillinger
- 1.3 Produkt av et reelt tall av en annen imaginær
- 1.4 Empowerment of an imaginary
- 1.5 Summen av et reelt tall og et imaginært tall
- 2 Søknader
- 3 Øvelser med imaginære tall
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 3.3 - Øvelse 3
- 3.4 - Øvelse 4
- 3.5 - Øvelse 5
- 3.6 - Øvelse 6
- 4 Referanser
Eiendommer
Settet med imaginære tall er betegnet med:
I = …, -3i,…, -2i,…., - i,…., 0i,…., I,…., 2i,…., 3i,…
Og du kan definere noen operasjoner på dette numeriske settet. Det oppnås ikke alltid et imaginært tall fra disse operasjonene, så la oss se litt nærmere på dem:
Addisjon og subtraksjon av imaginær
Imaginære tall kan legges til og trekkes fra hverandre, noe som resulterer i et nytt imaginært tall. For eksempel:
3i + 2i = 5i
4i - 7i = -3i
Produkt av imaginær
Når produktet av et imaginært nummer med et annet er laget, er resultatet et reelt tall. La oss gjøre følgende for å sjekke det:
2i x 3i = 6 x ito = 6 x (√ (-1))to = 6 x (-1) = -6.
Og som vi kan se, er -6 et reelt tall, selv om det er oppnådd ved å multiplisere to rene imaginære tall.
Produkt av et reelt tall av en annen imaginær
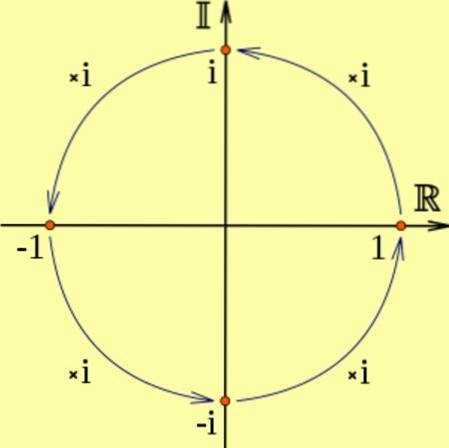
Hvis et reelt tall multipliseres med i, blir resultatet et imaginært tall, som tilsvarer en 90 graders rotasjon mot klokken.
Og det er at jegto tilsvarer to påfølgende rotasjoner på 90 grader, som tilsvarer å multiplisere med -1, det vil si ito = -1. Det kan sees i følgende diagram:
For eksempel:
-3 x 5i = -15i
-3 x i = -3i.
Empowerment of an imaginary
Du kan definere potensering av et imaginært tall til et heltall eksponent:
Jeg1 = i
Jegto = i x i = √ (-1) x √ (-1) = -1
Jeg3 = i x ito = -i
Jeg4 = ito x ito = -1 x -1 = 1
Jeg5 = i x i4 = i
Generelt må du Jegn = i ^ (n mod 4), hvor mod er resten av skillet mellom n Y 4.
Negativt heltalspotensiering kan også utføres:
Jeg-1 = 1 / i1 = i / (i x i1) = i / (ito) = i / (-1) = -i
Jeg-to = 1 / ito = 1 / (-1) = -1
Jeg-3= 1 / i3 = 1 / (- i) = (-1) / i = -1 x i-1 = (-1) x (-i) = i
Generelt sett er det imaginære tallet b⋅i hevet til kraften n:
(b⋅i) in = bn Jegn = bn i ^ (n mod 4)
Noen eksempler er følgende:
(5 i)12 = 512 Jeg12 = 512 Jeg0 = 512 x 1 = 244140625
(5 i)elleve = 5elleve Jegelleve = 5elleve Jeg3 = 5elleve x (-i) = -48828125 i
(-2 i)10 = -210 Jeg10 = 210 Jegto = 1024 x (-1) = -1024
Summen av et reelt tall og et imaginært tall
Når du legger til et reelt tall med et imaginært tall, er resultatet verken reelt eller imaginært, det er en ny type nummer som heter komplekst tall.
For eksempel, hvis X = 3,5 og Y = 3,75i, er resultatet det komplekse tallet:
Z = X + Y = 3,5 + 3,75 i
Merk at i summen kan ikke de virkelige og imaginære delene grupperes sammen, så et komplekst tall vil alltid ha en reell del og en imaginær del..
Denne operasjonen utvider settet med reelle tall til det bredeste av komplekse tall.
applikasjoner
Navnet på imaginære tall ble foreslått av den franske matematikeren René Descartes (1596-1650) som en hån eller uenighet med forslaget om det samme fra den italienske matematikeren Raffaelle Bombelli.
Andre store matematikere, som Euler og Leibniz, støttet Descartes i denne uenigheten og kalte imaginære tall amfibietall, som ble revet mellom å være og ingenting.
Navnet på imaginære tall forblir i dag, men deres eksistens og betydning er veldig reell og håndgripelig, siden de vises naturlig i mange fysikkfelt som:
-Relativitetsteorien.
-I elektromagnetisme.
-Kvantemekanikk.
Øvelser med imaginære tall
- Øvelse 1
Finn løsningene i følgende ligning:
zto + 16 = 0
Løsning
zto = -16
Tar kvadratrot i begge medlemmene har vi:
√ (zto ) = √ (-16)
± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i
Løsningene til den opprinnelige ligningen er med andre ord:
z = + 4i eller z = -4i.
- Øvelse 2
Finn resultatet av å heve den imaginære enheten til kraften 5 minus subtraksjonen til den imaginære enheten løftet til kraften -5.
Løsning
Jeg5 - Jeg-5 = i5 - 1 / i5 = i - 1 / i = i - (i) / (i x i) = i - i / (- 1) = i + i = 2i
- Øvelse 3
Finn resultatet av følgende operasjon:
(3i)3 + 9i
Løsning
33 Jeg3 - 9 = 9 (-i) + 9i = -9i + 9i = 0i
- Øvelse 4
Finn løsningene i følgende kvadratiske ligning:
(-2x)to + 2 = 0
Løsning
Ligningen omorganiseres som følger:
(-2x)to = -2
Deretter tas kvadratroten til begge medlemmene
√ ((- 2x)to) = √ (-2)
± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i
Deretter løser vi for x for å endelig oppnå:
x = ± √2 / 2 i
Det vil si at det er to mulige løsninger:
x = (√2 / 2) i
Eller denne andre:
x = - (√2 / 2) i
- Øvelse 5
Finn verdien av Z definert av:
Z = √ (-9) √ (-4) + 7
Løsning
Vi vet at kvadratroten til et negativt reelt tall er et imaginært tall, for eksempel er √ (-9) lik √ (9) x √ (-1) = 3i.
På den annen side er √ (-4) lik √ (4) x √ (-1) = 2i.
Så den opprinnelige ligningen kan erstattes av:
3i x 2i - 7 = 6 ito - 7 = 6 (-1) - 7 = -6 - 7 = -13
- Øvelse 6
Finn verdien av Z som følge av følgende inndeling av to komplekse tall:
Z = (9 - ito) / (3 + i)
Løsning
Telleren for uttrykket kan faktureres ved hjelp av følgende egenskap:
En forskjell i kvadrater er produktet av summen og forskjellen på binomialene uten kvadrat.
Deretter:
Z = [(3 - i) (3 + i)] / (3 + i)
Det resulterende uttrykket blir deretter forenklet og forlater
Z = (3 - i)
Referanser
- Earl, R. Komplekse tall. Gjenopprettet fra: maths.ox.ac.uk.
- Figuera, J. 2000. Matematikk 1.. Diversifisert. CO-BO utgaver.
- Hoffmann, J. 2005. Utvalg av matematikkemner. Monfort-publikasjoner.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Wikipedia. Fantasienummer. Gjenopprettet fra: en.wikipedia.org



Ingen har kommentert denne artikkelen ennå.