Endimensjonale bølger matematisk uttrykk og eksempler

De endimensjonale bølger De er de som forplanter seg i en enkelt retning, uavhengig av om vibrasjonen oppstår i samme retning av forplantning eller ikke. Et godt eksempel på dem er bølgen som beveger seg gjennom en stram streng som en gitar..

I en flat bølge kryss, partiklene vibrerer i vertikal retning (de går opp og ned, se den røde pilen i figur 1), men den er endimensjonal fordi forstyrrelsen bare beveger seg i én retning, etter den gule pilen.

Endimensjonale bølger vises ganske ofte i hverdagen. Følgende avsnitt beskriver noen eksempler på dem og også på bølger som ikke er endimensjonale, for å tydeliggjøre forskjellene.

Artikkelindeks

• 1 Eksempler på endimensjonale bølger og ikke-endimensjonale bølger
  • 1.1 Endimensjonale bølger
  • 1.2 Ikke-dimensjonale bølger
• 2 Matematisk uttrykk for en endimensjonal bølge
  • 2.1 En-dimensjonal bølgeligning
  • 2.2 Arbeidet eksempel
• 3 Referanser

Eksempler på endimensjonale bølger og ikke-dimensjonale bølger

Endimensjonale bølger

Her er noen eksempler på endimensjonale bølger som lett kan observeres:

- En lydpuls som beveger seg gjennom en rett stang, siden det er en forstyrrelse som forplanter seg hele stangen.

- En bølge som beveger seg gjennom en vannkanal, selv om forskyvningen av vannoverflaten ikke er parallell med kanalen.

- Bølger som forplanter seg på en overflate eller gjennom et tredimensjonalt rom, kan også være endimensjonale, så lenge bølgefrontene deres er planer parallelle med hverandre og bare beveger seg i en retning..

Ikke-dimensjonale bølger

Et eksempel på en ikke-dimensjonal bølge finnes i bølger som dannes på en stille vannflate når en stein faller. Det er en todimensjonal bølge med en sylindrisk bølgefront.

Et annet eksempel på en ikke-endimensjonal bølge er lydbølgen som en fyrverker genererer ved å eksplodere i en viss høyde. Dette er en tredimensjonal bølge med sfæriske bølgefronter.

Matematisk uttrykk for en endimensjonal bølge

Den mest generelle måten å uttrykke en endimensjonal bølge som forplanter seg uten demping i aksens positive retning x og med fart v er, matematisk:

y (x, t) = f (x - v.t)

I dette uttrykket Y representerer forstyrrelse i stillingen x Øyeblikkelig t. Formen på bølgen er gitt av funksjonen F. For eksempel er bølgefunksjonen vist i figur 1:  y (x, t) = cos (x - v t) og bølgebildet tilsvarer øyeblikket t = 0.

En bølge som denne, beskrevet av en cosinus eller sinusfunksjon, kalles harmonisk bølge. Selv om det ikke er den eneste bølgeformen som eksisterer, er den av største betydning, fordi enhver annen bølge kan representeres som en superposisjon eller sum av harmoniske bølger. Det handler om det kjente Fourier-setning, så brukt til å beskrive signaler av alle slag.

Når bølgen beveger seg i negativ retning av x-aksen, endres den ganske enkelt v til -v i argument, forlater:

y (x, t) = g (x + v t)

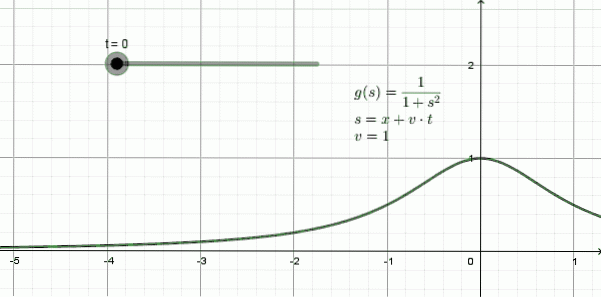
Figur 3 viser animasjonen av en bølge som beveger seg mot venstre: det er en form som kalles en funksjon lorentziana og henne matematisk uttrykk er:

y (x, t) = 1 / (1 + (x + 1)⋅t)^to

I dette eksemplet er forplantningshastigheten v = 1, -én enhet for hver tidsenhet-.

Endimensjonal bølgeligning

Bølge ligningen er en delvis avledet ligning, hvis løsning naturligvis er en bølge. Den etablerer det matematiske forholdet mellom den romlige delen og den tidsmessige delen av den, og har formen:

Arbeidet eksempel

Følgende er det generelle uttrykket y (x, t) for en harmonisk bølge:

y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)

a) Beskriv den fysiske betydningen av parametrene A, k, ω Y θo.

b) Hvilken betydning har ± tegnene i cosinusargumentet?

c) Bekreft at det gitte uttrykket faktisk er løsningen på bølgelikningen fra forrige avsnitt, og finn hastigheten v forplantning.

Løsning til)

Karakteristikken til bølgen finnes i følgende parametere:

-TIL representerer amplitude eller "bølgehøyde".

-hva er i bølgenummer og er relatert til bølgelengden λ gjennom k = 2π / λ.

-ω er fvinkelfrekvens og er relatert til periode T bølgesvingning av

ω = 2π / T.

-θo er den innledende fase, som er relatert til startpunktet for bølgen.

Løsning b)

Et negativt tegn tas hvis bølgen beveger seg i positiv retning av X-aksen og et positivt tegn ellers..

Løsning c)

Bekreft at det gitte uttrykket er en løsning av bølge ligningen er enkel: den delvise derivatet av funksjonen er tatt y (x, t) med hensyn til x to ganger, delvis avledet med hensyn til t to ganger, og kombiner deretter begge resultatene for å oppnå en likhet:

Andre avledet med hensyn til x: ∂^toy / ∂x^to= -K^to. TIL⋅cos (k⋅x ± ω⋅t + θo)

Andre avledede med hensyn til t: ∂^toy / ∂t^to= -Ω^to. TIL⋅cos (k⋅x ± ω⋅t + θo)

Disse resultatene er erstattet i bølge ligningen:

 -k^to. TIL⋅cos (k⋅x ± ω⋅t + θo) = (1 / v^to) (-ω^to. TIL⋅cos (k⋅x ± ω⋅t + θo))

Så mye TIL ettersom cosinus er forenklet, siden de vises på begge sider av likheten og argumentet til cosinus er det samme, reduseres uttrykket til:

-k^to = (1 / v^to) (-ω^to)

Som gjør det mulig å få en ligning for v i form av ω Y k:

v^to = ω^to / k^to

v = ± ω / k

Referanser

1. E-pedagogisk. Ligning av endimensjonale harmoniske bølger. Gjenopprettet fra: e-ducativa.catedu.es
2. Hjørnet av fysikk. Bølgeklasser. Gjenopprettet fra: fisicaparatontos.blogspot.com.
3. Figueroa, D. 2006. Waves and Quantum Physics. Serie: Physics for Science and Engineering. Redigert av Douglas Figueroa. Simon Bolivar University. Caracas Venezuela.
4. Physics Lab. Bølgebevegelse. Gjenopprettet fra: fisicalab.com.
5. Peirce, A. Forelesning 21: Den endimensjonale bølgelikningen: D'Alemberts løsning. Gjenopprettet fra: ubc.ca.
6. Bølge ligning. Gjenopprettet fra: en.wikipedia.com