De egenskaper av likhet referere til forholdet mellom to matematiske objekter, enten de er tall eller variabler. Det er betegnet med "=" symbolet, som alltid går midt i disse to objektene. Dette uttrykket brukes til å fastslå at to matematiske objekter representerer det samme objektet; i et annet ord, at to objekter er det samme.
Det er tilfeller der det er trivielt å bruke likeverd. For eksempel er det klart at 2 = 2. Men når det gjelder variabler, er det ikke lenger trivielt og har spesifikke bruksområder. Hvis vi for eksempel har at y = x og på den annen side x = 7, kan vi konkludere med at y = 7 også.
Ovennevnte eksempel er basert på en av egenskapene til likhet, som du vil se om kort tid. Disse egenskapene er essensielle for å løse ligninger (likheter som involverer variabler), som utgjør en veldig viktig del i matematikk..
Artikkelindeks
Den refleksive egenskapen, i tilfelle av likhet, sier at hvert tall er lik seg selv og uttrykkes som b = b for ethvert reelt tall b.
I det spesielle tilfellet av likhet synes denne egenskapen å være åpenbar, men i andre typer forhold mellom tall er det ikke. Med andre ord oppfyller ikke alle reelle tallforhold denne egenskapen. For eksempel et slikt tilfelle av forholdet "mindre enn" (<); ningún número es menor que sí mismo.
Den symmetriske egenskapen for likhet sier at hvis a = b, så b = a. Det spiller ingen rolle rekkefølgen som brukes i variablene, den vil bli bevart av likhetsforholdet.
En viss analogi av denne egenskapen med kommutativ egenskap kan observeres i tilfelle tillegg. På grunn av denne egenskapen tilsvarer det for eksempel å skrive y = 4 eller 4 = y.
Den transitive egenskapen på likhet sier at hvis a = b og b = c, så a = c. For eksempel 2 + 7 = 9 og 9 = 6 + 3; Derfor har vi den transitive egenskapen at 2 + 7 = 6 + 3.
En enkel applikasjon er følgende: anta at Julian er 14 år og at Mario er i samme alder som Rosa. Hvis Rosa er like gammel som Julian, hvor gammel er Mario?
Bak dette scenariet brukes den transitive egenskapen to ganger. Matematisk tolkes det slik: la “a” være Mario-alderen, “b” Rosa-alderen og “c” Julian-alderen. Det er kjent at b = c og at c = 14.
Ved den transitive egenskapen har vi at b = 14; det vil si at Rosa er 14 år gammel. Siden a = b og b = 14, ved å bruke den transitive egenskapen igjen, har vi at a = 14; det vil si at Marios alder også er 14 år gammel.
Den ensartede egenskapen er at hvis begge sider av en likhet legges til eller multipliseres med samme beløp, blir likheten bevart. For eksempel, hvis 2 = 2, så er 2 + 3 = 2 + 3, noe som er klart, siden 5 = 5. Denne egenskapen er mest nyttig når du prøver å løse en ligning.
Anta for eksempel at du blir bedt om å løse ligningen x-2 = 1. Det er praktisk å huske at å løse en ligning består i eksplisitt å bestemme variabelen (eller variablene) som er involvert, basert på et bestemt tall eller en tidligere spesifisert variabel..
Å gå tilbake til ligningen x-2 = 1, hva du trenger å gjøre er å finne eksplisitt hvor mye x er verdt. For dette må variabelen tømmes.
Det er feilaktig blitt undervist i at i dette tilfellet, siden tallet 2 er negativt, går det til den andre siden av likheten med et positivt tegn. Men det er ikke riktig å si det slik.
I utgangspunktet er det du gjør å bruke den uniforme eiendommen, som vi vil se nedenfor. Tanken er å fjerne "x"; la det være på den ene siden av ligningen. Etter konvensjon er det vanligvis igjen på venstre side.
For dette formålet er tallet å "eliminere" -2. Måten å gjøre det på vil være ved å legge til 2, siden -2 + 2 = 0 og x + 0 = 0. For å kunne gjøre dette uten å endre likestillingen, må den samme operasjonen brukes på den andre siden.
Dette gjør det mulig å realisere den uniforme egenskapen: siden x-2 = 1, hvis tallet 2 legges til på begge sider av likheten, sier den uniforme egenskapen at den ikke er endret. Så har vi den x-2 + 2 = 1 + 2, som tilsvarer å si at x = 3. Med dette ville ligningen bli løst.
På samme måte, hvis du vil løse ligningen (1/5) y-1 = 9, kan du fortsette å bruke den uniforme egenskapen som følger:
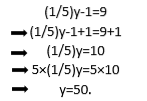
Mer generelt kan følgende uttalelser komme:
- Hvis a-b = c-b, så a = c.
- Hvis x-b = y, så x = y + b.
- Hvis (1 / a) z = b, så z = a ×
- Hvis (1 / c) a = (1 / c) b, så a = b.
Kanselleringsegenskapen er et spesielt tilfelle av den uniforme eiendommen, spesielt med tanke på subtraksjon og deling (som i utgangspunktet også tilsvarer addisjon og multiplikasjon). Denne eiendommen behandler denne saken separat.
For eksempel, hvis 7 + 2 = 9, så 7 = 9-2. Eller hvis 2y = 6, så y = 3 (delt med to på begge sider).
Analogt med den forrige saken kan følgende uttalelser fastslås gjennom kanselleringseiendommen:
- Hvis a + b = c + b, så a = c.
- Hvis x + b = y, så x = y-b.
- Hvis az = b, så z = b / a.
- Hvis ca = cb, så a = b.
Hvis vi vet verdien av et matematisk objekt, sier substitusjonsegenskapen at denne verdien kan erstattes i hvilken som helst ligning eller et uttrykk. For eksempel, hvis b = 5 og a = bx, og deretter erstatte verdien av "b" i den andre likheten, har vi at a = 5x.
Et annet eksempel er følgende: Hvis "m" deler "n" og også "n" deler "m", må den ha at m = n.
Å si at "m" deler "n" (eller tilsvarende, at "m" er en divisor av "n") betyr faktisk at divisjonen m ÷ n er nøyaktig; det vil si å dele "m" med "n" et helt tall, ikke et desimal. Dette kan uttrykkes ved å si at det eksisterer et helt tall "k" slik at m = k × n.
Siden "n" også deler "m", eksisterer det et helt tall "p" slik at n = p × m. På grunn av substitusjonsegenskapen har vi at n = p × k × n, og for at dette skal skje er det to muligheter: n = 0, i så fall vil vi ha identiteten 0 = 0; eller p × k = 1, derav identiteten n = n.
Anta at "n" ikke er null. Da nødvendigvis p × k = 1; derfor er p = 1 og k = 1. Ved å bruke substitusjonsegenskapen igjen, når vi erstatter k = 1 i likheten m = k × n (eller tilsvarende, p = 1 i n = p × m), får vi endelig at m = n, som var det vi ønsket å demonstrere.
Akkurat som tidligere ble det sett at hvis en operasjon som tillegg, multiplikasjon, subtraksjon eller divisjon gjøres i begge termer av en likhet, bevares den, på samme måte kan andre operasjoner som ikke endrer en likhet, brukes.
Nøkkelen er å alltid utføre den på begge sider av likestillingen og på forhånd sørge for at operasjonen kan utføres. Slik er tilfellet med empowerment; det vil si at hvis begge sider av en ligning heves til samme kraft, har vi fortsatt likhet.
For eksempel, siden 3 = 3, så 3to= 3to (9 = 9). Generelt gitt et helt tall "n", hvis x = y, så xn= ogn.
Dette er et spesielt tilfelle av empowerment og brukes når kraften er et ikke-helt rasjonelt tall, slik som ½, som representerer kvadratroten. Denne egenskapen sier at hvis den samme roten brukes på begge sider av en likhet (når det er mulig), er likheten bevart.
I motsetning til det forrige tilfellet, må man være forsiktig med pariteten til roten som skal brukes, siden det er velkjent at den jevne roten til et negativt tall ikke er godt definert.
I tilfelle at det radikale er jevnt, er det ikke noe problem. For eksempel hvis x3= -8, selv om det er en likhet, kan du ikke bruke en kvadratrot på begge sider, for eksempel. Men hvis du kan bruke en kuberot (som er enda mer praktisk hvis du eksplisitt vil vite verdien av x), og dermed oppnå at x = -2.
Ingen har kommentert denne artikkelen ennå.