
Kartografiske fremskrivninger hva de er for og typer

De kartografiske anslag er representasjoner på et plan av punktene som er på overflaten av jorden, som er buet. På denne måten konverteres koordinatene til et sted: breddegrad og lengdegrad, til et punkt med kartesiske koordinater x og y.
Selvfølgelig er dette ikke lett, da dette betyr "flating" av jordkulen, noe som ikke kan gjøres uten deformasjon. Dette er faktisk det som skjer på de fleste kart.
Leseren kan prøve å fjerne skallet midt i en appelsin og deretter prøve å gjøre det helt flatt. Den eneste måten å oppnå dette på er å bryte det i noen deler, men på denne måten er det klart at overflaten deformeres ganske mye..
Av denne grunn sammenfaller verken lengdene, retningene eller formene som er representert på kartene nøyaktig med de virkelige, eller i det minste ikke alle disse egenskapene samtidig. Når en av dem blir bevart, går den andre på en eller annen måte tapt, i det minste delvis. Avhengig av formålet med kartet, kan slike tap imidlertid være akseptable..
Til tross for dette har flate fremstillinger av jordoverflaten mange fordeler. For det første er kart bærbare og kan tas med mange steder uten å ta for mye plass.
I tillegg kan de lages spesielt for visse regioner og forstørre detaljene som anses som viktige, og minimere deformasjon. Dette er ikke gjennomførbart med en mer realistisk representasjon, som nødvendigvis er mindre: en klode å skalere..
Globus er bygget etter jordens form, men av størrelsesårsaker kan de ikke inneholde mye informasjon.
Artikkelindeks
- 1 Typer kartprojeksjoner
- 1.1 - I henhold til de bevarte egenskapene til projeksjonen
- 1.2 - I henhold til figuren som den er projisert på
- 2 Mest populære kartografiske anslag
- 2.1 Mercator-projeksjon
- 2.2 Lambert konisk projeksjon
- 3 Modifiserte kartprojeksjoner
- 3.1 Sinusformet projeksjon
- 3.2 Mollweide-projeksjon
- 3.3 God projeksjon
- 4 Referanser
Typer kartprojeksjoner
- I henhold til de bevarte egenskapene til projeksjonen
Avhengig av egenskapene som er bevart i projeksjonen, er det følgende typer kartografiske fremskrivninger:
-I henhold: opprettholder de eksisterende vinklene mellom to linjer på jordoverflaten, derfor er det en passende projeksjon for navigasjonskart
-Tilsvarende (like-areal): Denne projeksjonen holder terrengoverflatene riktige, selv om deformasjon kan oppstå og formene ikke lenger er like. Det er riktig projeksjon for pakkekart.
-Like langt: som navnet antyder, holdes avstandene mellom to punkter i denne projeksjonen identiske, sammenføyd av en bue på jordoverflaten og av en rett linje på kartet.
-Fylaktisk- Vinkler, overflater og avstander er ikke bevart i denne projeksjonen, men formforvrengning er minimal.
- I henhold til figuren som den er projisert på
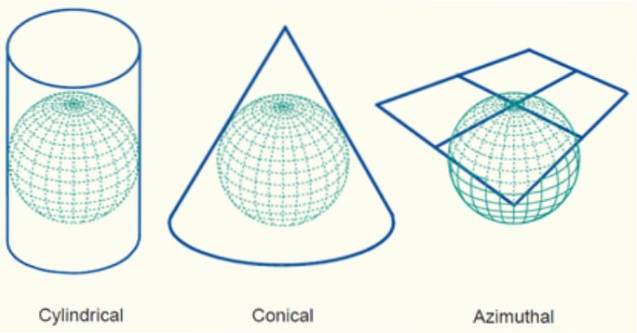
Det er mange, mange måter å lage fremskrivninger på. Et annet mye brukt kriterium er å klassifisere i henhold til planfiguren som den projiseres på, som for eksempel kan være et plan, en sylinder eller en kjegle..
Når du bruker et fly, kalles projeksjonen projeksjon av plan eller azimut, mens når en geometrisk figur brukes, er den en vekst, fordi den geometriske figuren kan utvikle seg senere til å bli et plan, som vi vil se nedenfor.
Plan- eller azimutale projeksjoner
De er bygget fra projeksjonen av jordoverflaten fra et punkt kjent som projeksjon toppunkt, mot et plan som tangerer jordoverflaten. Tangenspunktet kalles projeksjonssenter.
Denne typen projeksjon har flere varianter, avhengig av plasseringen av både projeksjonspunktet og tangenspunktet til planet..
Konisk projeksjon
Kjeglen og sylinderen er de geometriske figurene som mest brukes som hjelpemidler for å utvikle projeksjonen. I det første tilfellet, konisk projeksjon, sfæren er dekket av en kjegle, hvis symmetriakse går gjennom polene.
Nå, på jordoverflaten, trekkes buede linjer for å plassere hvert punkt: parallellene og meridianene. Når du projiserer på kjeglen, vises parallellene som konsentriske sirkler, mens meridianene vises som samtidige linjer i toppunktet til kjeglen.
Sylindrisk projeksjon
I sylindrisk projeksjon, jordoverflaten er dekket av en sylinder som tangerer sfæren, og sylinderen er parallell med aksen som går gjennom polene. Deretter forlenges sylinderen, hvor meridianene og parallellene forblir som rette linjer.
Linjene som tilsvarer meridianene vil være like store, men ikke de som tilsvarer parallellene, hvis avstand øker når lengdegraden øker..
Imidlertid kan sylinderen plasseres på en annen måte, og ikke nødvendigvis berøre jordoverflaten på ekvator, som vist på figuren. Sylinderen kan ha en diameter som er mindre enn jordens.
Mest populære kartprojeksjoner
Type projeksjoner beskrevet ovenfor kan kombineres for å danne nye projeksjoner. De mest kjente er kort beskrevet nedenfor..
Mercator-projeksjon
Det er blant de mest brukte anslagene for å representere verdenskart. Den ble oppfunnet av geografen Gerard Kremer, også kjent som Gerardus Mercator (1512-1594) i år 1569.
Det er en samsvarende sylindrisk projeksjon, det vil si at den respekterer vinklene, og det er derfor det er en projeksjon som er veldig verdsatt av seilere. Imidlertid bevarer den ikke områder, da denne typen projeksjon er passende for ekvatoriale områder. Utenfor disse breddegradene ser regionene mye større ut enn de egentlig er.
Til tross for disse ulempene er det projeksjonen som brukes i de mest populære kartapplikasjonene på internett..
Lambert konisk projeksjon
Denne projeksjonen ble skapt av den sveitsiske matematikeren Johann Lambert (1728-1777), som også viste at tallet π er irrasjonelt. Denne projeksjonen bevarer avstander veldig bra og er veldig egnet for å representere mellombreddegrader, men den er ikke egnet for ekvatoriale breddegrader på grunn av deformasjon..
Modifiserte kartprojeksjoner
Denne gruppen projeksjoner brukes til å representere jordoverflaten, og prøver å minimere deformasjoner. Blant de mest kjente er:
Sinusformet projeksjon
Denne projeksjonen gjør at parallellene kan være horisontale og like store, i motsetning til den sylindriske projeksjonen. Den sentrale meridianen er en linje vinkelrett på parallellene, men de andre meridianene kurver rundt.
Avstandene mellom parallellene, så vel som mellom parallellene og den sentrale meridianen er sanne, og den bevarer også områdene.
Mollweide projeksjon
Denne projeksjonen søker å bevare områdene. Her er ekvator dobbelt så lang som den sentrale meridianen. Meridianene har form av ellipser, og parallellene er horisontale linjer parallelt med ekvator, hvis separasjon avhenger av trofast bevaring av områdene, og er veldig passende for mellomstore breddegrader..
Goode projeksjon
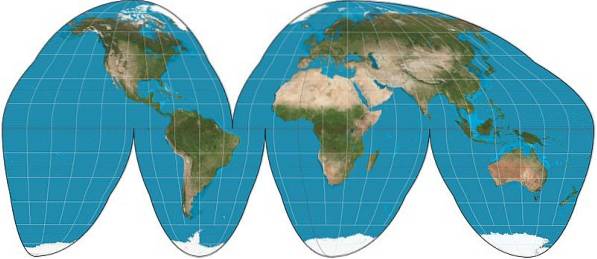
Dette er en projeksjon som, i motsetning til de forrige, er diskontinuerlig. I den er jordoverflaten representert i form av uregelmessige og forente områder, noe som minimerer forvrengningen på kontinentene. Ikke så i havoverflater, som er delt, som det fremgår av figuren.
Imidlertid har Goode-projeksjonen fordelen av å bevare formen på kontinentene og også områdene, og det er derfor den er mye brukt i økonomiske kart for å representere distribusjonen av produkter over hele verden..
Referanser
- Aguilar, A. 2004. Generell geografi. 2. plass. Utgave. Pearson Education.
- Gisgeography. Hva er kartprojeksjoner? Gjenopprettet fra: gisgeography.com
- Snaider, P. Kartografiske projeksjoner og referansesystemer. Gjenopprettet fra: hum.unne.edu.ar.
- USGS. Kartprojeksjoner. Gjenopprettet fra: icsm.gov.au
- Wikipedia. Liste over kartprojeksjoner. Gjenopprettet fra: en.wikipedia.com



Ingen har kommentert denne artikkelen ennå.