Hva er trekantetall? Eiendommer og demonstrasjoner

Det er kjent som trekantede tall til rekkefølgen av tall som oppnås ved å lage en ordning eller figur av punkter i form av en ligesidig trekant. De første i sekvensen er: 1, 3, 6, 10, 15, 21, ...

Det første trekantet tallet er 1, det andre er 3, fordi det oppnås ved å legge til en rad med to punkter til den forrige, for å danne en ensidig trekant av tre elementer.

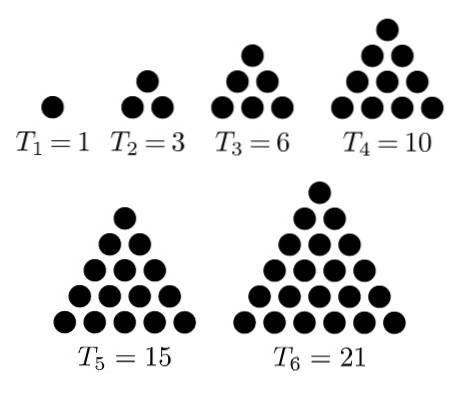
Den tredje er 6, som vises når du legger til en rad med tre punkter til forrige arrangement, på en slik måte at det dannes en trekant på tre punkter per side. 10 av sekvensen oppnås ved å legge til en annen rad i det forrige arrangementet slik at det dannes en trekant på fire punkter per side.

Formelen som gjør det mulig å finne elementet n av den trekantede sekvensen, kjent forrige trekantnummer er:

T_n = T_n-1 + n

Listen over de seks første trekantnumrene er oppnådd slik:

-Først: 1

-Sekund: 1 + 2 = 3

-Tredje: (1 +2) + 3 = 3 + 3 = 6

-Soverom: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Femte: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Sjette: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

Artikkelindeks

• 1 Egenskaper til trekantetall
• 2 demonstrasjoner
  • 2.1 - Demo 1
  • 2.2 - Demo 2
  • 2.3 - Demo 3
  • 2.4 - Demonstrasjon 5
• 3 Referanser

Egenskaper av trekantede tall

1. - Det niende trekantsnummeret Tn i sekvensen av trekanttall er halvparten av n multiplisert med n + 1:

T_n = ½ n (n + 1)

2. - Summen av det niende trekantnummeret med det forrige trekantnummeret, det vil si (n-1) -te, er n kvadrat:

T_n + T_n-1= n^to

3.- Forskjellen på det n-th trekantetallet minus den n-th trekantet minus en er n:

T_n - T_n-1 = n

4. - Summen av de første n trekanttallene kalles tetraedretallet Sn og er lik den sjette delen av produktet av n multiplisert med (n + 1) og ganget med (n + 2):

S_n= ⅙ n (n + 1) (n + 2)

5.- Hvert naturlige tall N er resultatet av summen av tre trekantede tall:

N = A1 + A1 + A3

Denne siste eiendommen eller teoremet ble oppdaget av den store matematikeren Carl Friedrich Gauss i 1796, som han bemerket i sin dagbok og plasserte den greske beundringen. Eureka! hva betyr det "Jeg har gjort det".

Det var det samme ordet som den greske arkimedes brukte lenge da han bestemte den tilsynelatende vekten til et nedsenket legeme..

I dette forholdet blir tallet null tatt som trekantet, og det kan være repetisjon.

Demonstrasjoner

- Demo 1

Bevis at det trekantede tallet n-th er:

T_n = ½ n (n + 1)

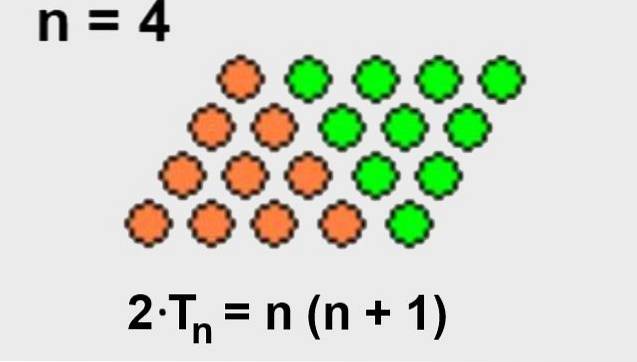
Det er lett å utlede formelen ovenfor, hvis vi innser at vi kan legge til like mange poeng i det trekantede arrangementet slik at det danner en firkant av punkter.

Siden det totale antall poeng i den firkantede ordningen er antall rader n multiplisert med antall kolonner (n + 1), da vil det trekantede arrangementet bare ha halvparten av punktene i det firkantede arrangementet.

Her er det illustrert i figur 2.

- Demo 2

Vis at summen av n-trekantnummer med n-th minus en trekantet tall er n kvadrat:

T_n + T_n-1= n^to

Det er allerede vist at det trekantede tallet n-th er gitt av:

T_n= ½ n (n + 1)

Derfor er det trekantede tallet over:

T_n-1 = ½ (n-1) ((n-1) + 1) = ½ n (n - 1)

Summen av begge er:

T_n + T_n-1 = ½ n (n + 1) + ½ n (n - 1)

Den vanlige faktoren ½ n er tatt for å oppnå:

T_n + T_n-1 = ½ n [(n + 1) + (n - 1)] = ½ n [n + 1 + n - 1]

Og straks forenkles uttrykket inne i braketten:

T_n + T_n-1 = ½ n [2 n] = ½ 2 n ⋅ n

Nå som vi husker at ½ ganger 2 er 1 og at n ganger n er n kvadrat, har vi:

T_n + T_n-1 = n^to

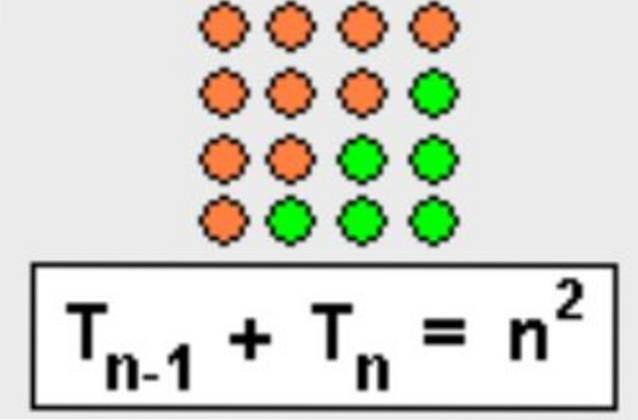
Denne egenskapen kan også demonstreres i geometrisk form, bare fullfør trekanten for å danne en firkant, som vist i figur 3.

- Demo 3

Forskjellen på det trekantede ordrenummeret n minus det trekantede ordrenummeret n-1 er n:

T_n - T_n-1 = n

Dette kan bevises ganske enkelt ved å huske at følgende trekantnummer er oppnådd fra forrige ved hjelp av formelen:

T_n = T_n-1 + n

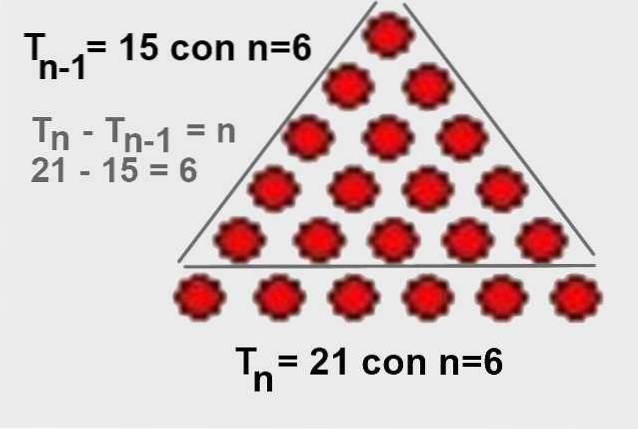
Og derfra er det tydelig at T_n - T_n-1 = n. Det er også enkelt å visualisere det grafisk, som vist i figur 4.

- Demo 5

Summen av de første n trekantnumrene Sn er lik en sjettedel av produktet av n multiplisert med (n + 1) og multiplisert med (n + 2):

S_n = ⅙ n (n + 1) (n + 2)

La oss bruke det trekantede antallet ordre n: T_n= ½ n (n + 1). Summen av den første n trekantede tall betegner det med S_n  

For eksempel, S₁ betyr summen av det første trekantet tallet, som utvilsomt vil være 1.

Deretter, la oss se om formelen vi prøver å teste er sant for n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Faktisk er formelen for n = 1 bekreftet. Det er lett å visualisere at summen av de første n + 1 trekantnumrene vil være summen av den første n pluss det neste trekantede tallet:

S_{n + 1} = S_n + T_{n + 1}

Anta nå at formelen for S_n er sant for n, så erstatter vi det i forrige uttrykk og legger til det trekantede rekkefølgen n + 1:

S_{n + 1} = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]

La oss se trinn for trinn hva du får:

-Vi utfører summen av de to brøkuttrykkene:

S_{n + 1} = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] / 12 

-Det er tatt fra tellerens fellesfaktor til 2 (n + 1) (n + 2) og forenkler:

S_{n + 1} = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Ovennevnte resultat stemmer overens med formelen for Sn hvis n erstattes av n + 1, noe som er vist ved induksjon formelen for summen av de første n trekantede begrepene.

Tetrahedral nummer

Resultatet som oppnås på denne måten kalles tetraedrisk antall ordre n, fordi det er som å samle trekantede lag som danner et tetraeder, som vist i den følgende animasjonen.

Referanser

1. Camacho J. Et uventet utseende av trekantede tall. Gjenopprettet fra: masscience.com
2. Claudio. Trekantetall. Gjenopprettet fra: ganske enkelt tall. blogspot. com
3. Wikipedia. Trekantetall. Gjenopprettet fra: es.wikipedia.com
4. Wikipedia. Trekantetall. Gjenopprettet fra: en.wikipedia.com
5. Wikipedia. Tretrahedral nummer. Gjenopprettet fra: en.wikipedia.com