
Høyrehåndsregel første og andre regel, applikasjoner, øvelser

De høyre håndregel er en mnemonisk ressurs for å etablere retning og følelse av vektoren som følge av et vektorprodukt eller kryssprodukt. Det er mye brukt i fysikk, siden det er viktige vektormengder som er resultatet av et vektorprodukt. Slik er for eksempel dreiemoment, magnetisk kraft, vinkelmoment og magnetisk moment.
La være to generiske vektorer til Y b hvis kryssprodukt er til x b. Modulen til en slik vektor er:
til x b = a.b. i α
Hvor α er minimumsvinkelen mellom til Y b, mens a og b representerer modulene. For å skille ut vektorene til modulene deres, brukes fete bokstaver.
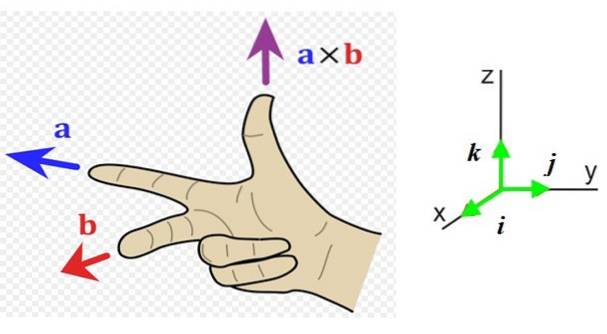
Nå må vi vite retningen og følelsen av denne vektoren, så det er praktisk å ha et referansesystem med de tre retningene i rommet (figur 1 til høyre). Enhetsvektorene Jeg, j Y k de peker henholdsvis mot leseren (utenfor siden), til høyre og opp.
I eksemplet i figur 1 til venstre, vektoren til hodet til venstre (retning Y negativ og pekefinger på høyre hånd) og vektoren b går til leseren (retning x positiv, langfinger på høyre hånd).
Den resulterende vektoren til x b har tommelretningen, opp i retningen z positivt.
Artikkelindeks
- 1 Andre regel på høyre hånd
- 1.1 Alternativ regel for høyre hånd
- 2 Søknader
- 2.1 Vinkelhastighet og akselerasjon
- 2.2 Vinkelmomentet
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referanser
Andre regel på høyre hånd
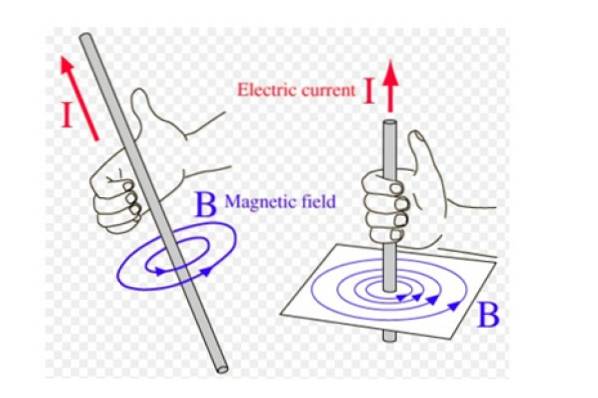
Denne regelen, også kalt høyre tommelfingerregel, Det brukes mye når det er størrelser hvis retning og retning roterer, for eksempel magnetfeltet B produsert av en tynn, rett ledning som bærer en strøm.
I dette tilfellet er magnetfeltlinjene konsentriske sirkler med ledningen, og rotasjonsretningen oppnås med denne regelen på følgende måte: høyre tommel peker i strømens retning og de resterende fire fingrene er buet i retning av landsbygda. Vi illustrerer konseptet i figur 2.
Alternativ høyre håndregel
Figuren nedenfor viser en alternativ form for høyre-regelen. Vektorene som vises i illustrasjonen er:
-Hastighet v av en punktladning q.
-Magnetfelt B der lasten beveger seg.
-FB kraften som magnetfeltet utøver på ladningen.
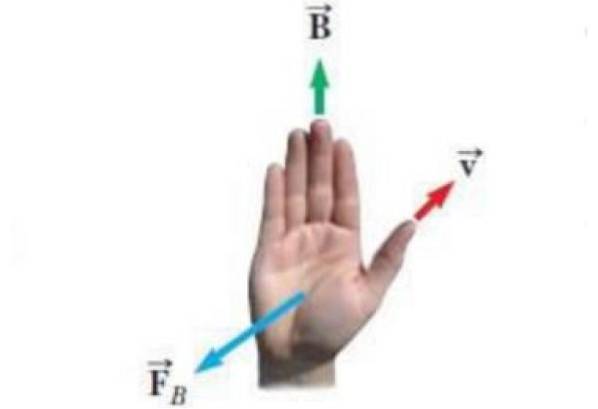
Ligningen for magnetkraften er FB = qv x B og regelen om høyre hånd for å kjenne retningen og følelsen av FB påføres slik: tommelen peker i henhold til v, de fire gjenværende fingrene plasseres i henhold til felt B. Deretter FB er en vektor som kommer ut av håndflaten, vinkelrett på den, som om den skyver belastningen.
Noter det FB Jeg vil peke i motsatt retning hvis ladningen q var negativ, siden vektorproduktet ikke er kommutativt. Faktisk:
til x b = - b x til
applikasjoner
Høyrehåndsregelen kan brukes på forskjellige fysiske størrelser, la oss kjenne noen av dem:
Vinkelhastighet og akselerasjon
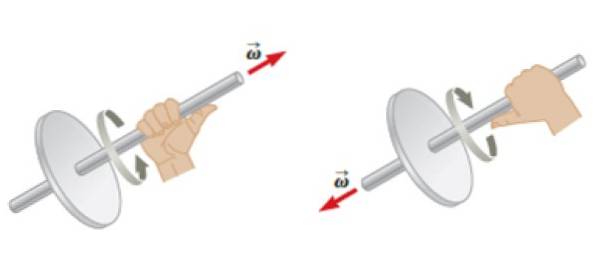
Begge vinkelhastighetene ω som vinkelakselerasjon α de er vektorer. Hvis et objekt roterer rundt en fast akse, er det mulig å tilordne retningen og følelsen av disse vektorene ved hjelp av høyre håndregel: de fire fingrene krølles etter rotasjonen, og tommelen gir umiddelbart retningen og følelsen av vinkelhastighet ω.
For sin del vinkelakselerasjonen α vil ha samme adresse som ω, men betydningen avhenger av om ω øker eller avtar i størrelse over tid. I det første tilfellet har begge samme retning og forstand, men i det andre vil de ha motsatte retninger..
Vinkelmoment
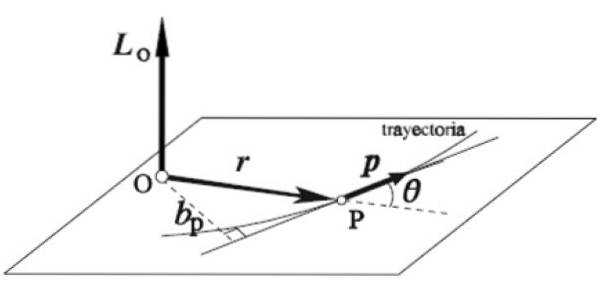
Vinkelmomentvektoren LELLER av en partikkel som roterer rundt en bestemt akse O er definert som vektorproduktet til dets øyeblikkelige posisjonsvektor r og det lineære momentum s:
L = r x s
Regelen på høyre hånd brukes på denne måten: pekefingeren er plassert i samme retning og følelse av r, langfingeren på den av s, begge på et horisontalt plan, som på figuren. Tommelen utvides automatisk vertikalt oppover, noe som indikerer retningen og følelsen av vinkelmoment LELLER.
Opplæring
- Øvelse 1
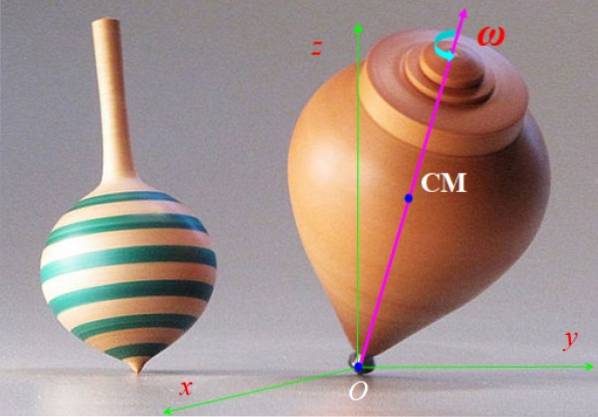
Toppen i figur 6 snurrer raskt med vinkelhastighet ω og symmetriaksen roterer saktere rundt den vertikale aksen z. Denne bevegelsen kalles presesjon. Beskriv kreftene som virker på snurretoppen og effekten de gir.
Løsning
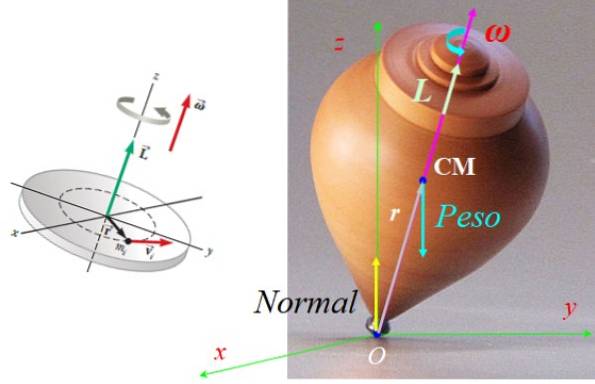
Kreftene som virker på toppen er normale N, påført på støttepunktet med bakken O pluss vekten Mg, påført i sentrum av massen CM, med g akselerasjonsvektoren for tyngdekraften, rettet vertikalt nedover (se figur 7).
Begge kreftene balanserer, derfor beveger ikke toppen seg. Vekten gir imidlertid et dreiemoment eller dreiemoment τ netto med hensyn til punkt O, gitt av:
τELLER = rELLER x F, med F = Mg.
Hva r og Mg de er alltid i samme plan som toppen roterer, i henhold til høyre styremoment τELLER ligger alltid på flyet xy, vinkelrett på begge deler r Hva g.
Noter det N produserer ikke et dreiemoment i forhold til O, fordi dens vektor r med hensyn til O er null. Dette dreiemomentet gir en endring i vinkelmomentet som får toppen til å gå foran Z-aksen..
- Øvelse 2
Angi retning og følelse av vinkelmomentvektoren L på toppen av figur 6.
Løsning
Ethvert punkt på toppen har masse mJeg, hastighet vJeg og posisjonsvektor rJeg, når den roterer rundt z-aksen. Vinkelmoment LJeg av nevnte partikkel er:
LJeg = rJeg x sJeg = rJeg x mJegvJeg
Gitt rJeg Y vJeg er vinkelrett, størrelsen på L Det er:
LJeg = mJegrJegvJeg
Lineær hastighet v er relatert til vinkelhastigheten ω gjennom:
vJeg = rJegω
Derfor:
LJeg = mJegrJeg (rJegω) = mJegrJegtoω
Den totale vinkelmomentet til snurretoppen L er summen av vinkelmomentet til hver partikkel:
L = (∑mJegrJegto ) ω
∑ mJegrJegto er treghetsøyeblikket I av toppen, da:
L= Jegω
Derfor L Y ω har samme retning og sans, som vist i figur 7.
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Kirkpatrick, L. 2007. Fysikk: En titt på verden. 6. forkortet utgave. Cengage læring.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1 og 2. 7.. Ed. Cengage Learning.



Ingen har kommentert denne artikkelen ennå.