
Aksiale symmetriegenskaper, eksempler og øvelser
De aksial symmetri Det skjer når punktene i en figur sammenfaller med punktene i en annen figur ved hjelp av en rett halveringslinje kalt symmetriaksen. Det kalles også radial, roterende eller sylindrisk symmetri..
Det brukes vanligvis i geometriske figurer, men det er lett å observere i naturen, siden det er dyr som sommerfugler, skorpioner, marihøner eller mennesker som presenterer aksial symmetri..

Artikkelindeks
- 1 Hvordan finne den aksiale symmetriske
- 2 Egenskaper for aksial symmetri
- 3 Eksempler på aksial symmetri
- 4 Aksiale symmetriøvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 4.3 Øvelse 3
- 4.4 Øvelse 4
- 5 Referanser
Hvordan finne aksial symmetrisk
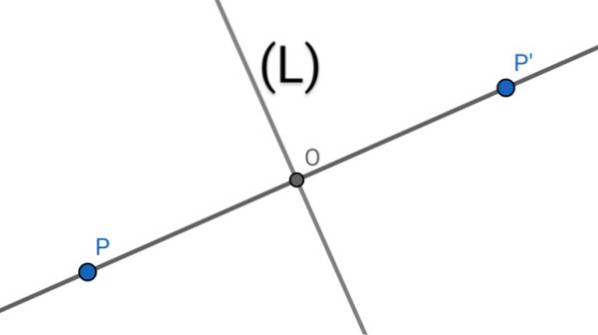
For å finne den aksiale symmetrien P 'til et punkt P i forhold til en linje (L), utføres følgende geometriske operasjoner:
1.- Vinkelrett på linjen (L) som går gjennom punkt P er tegnet.
2. - Avskjæringen av de to linjene bestemmer et punkt O.
3.- Lengden på segmentet PO måles, deretter kopieres denne lengden over linjen (PO) fra O i retning fra P til O som bestemmer punktet P '.
4.- Punkt P 'er den aksiale symmetriske for punktet P i forhold til aksen (L), siden linjen (L) er mediatrisen til segmentet PP', hvor O er midtpunktet til nevnte segment.
Egenskaper ved aksial symmetri
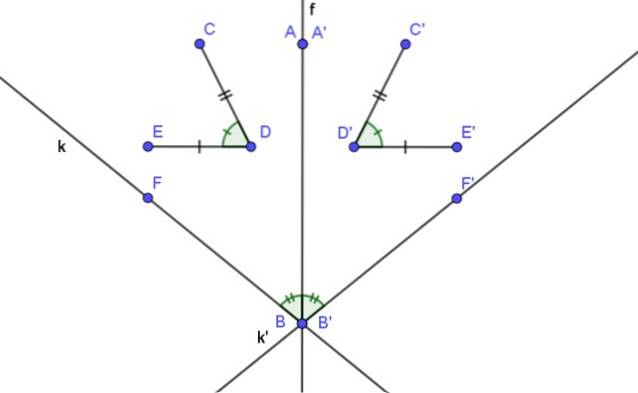
- Aksial symmetri er isometrisk, det vil si avstandene til en geometrisk figur og dens tilsvarende symmetri er bevart.
- Målene på en vinkel og symmetrisk er like.
- Den aksiale symmetrien til et punkt på symmetriaksen er selve punktet.
- Den symmetriske linjen til en linje parallell med symmetriaksen er også en linje parallell med aksen.
- En sekantlinje til symmetriaksen har som en symmetrisk linje en annen sekantlinje som i sin tur krysser symmetriaksen på samme punkt som den opprinnelige linjen.
- Det symmetriske bildet av en linje er en annen linje som danner en vinkel med symmetriaksen av samme mål som den opprinnelige linjen.
- Det symmetriske bildet av en linje vinkelrett på symmetriaksen er en annen linje som overlapper den første.
- En linje og dens aksiale symmetriske linje danner en vinkel hvis halveringslinje er symmetriaksen.
Eksempler på aksial symmetri
Naturen viser mange eksempler på aksial symmetri. For eksempel kan du se symmetri av ansikter, insekter som sommerfugler, refleksjonen på rolige vannflater og speil eller bladene til planter, blant mange andre..


Aksiale symmetriøvelser
Øvelse 1
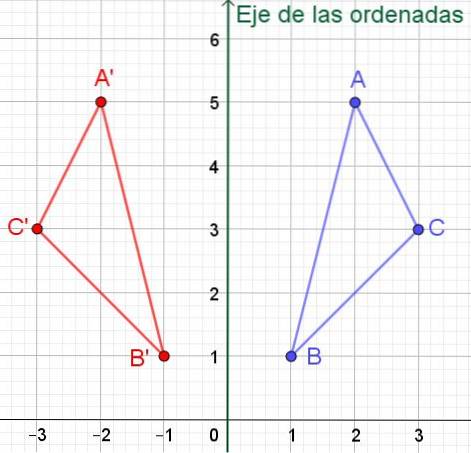
Vi har trekanten av hjørnene A, B og C hvis kartesiske koordinater er henholdsvis A = (2, 5), B = (1, 1) og C = (3,3). Finn de kartesiske koordinatene til trekanten symmetrisk rundt Y-aksen (ordinataksen).
Løsning: Hvis et punkt P har koordinater (x, y), er det symmetrisk rundt ordinataksen (Y-aksen) P '= (- x, y). Det vil si at verdien av abscissen endrer tegn, mens ordinatens verdi forblir den samme.
I dette tilfellet vil den symmetriske trekanten med hjørnene A ', B' og C 'ha koordinater:
A '= (- 2, 5); B '= (- 1, 1) og C' = (- 3, 3) som kan sees i figur 6.
Øvelse 2
Med henvisning til trekanten ABC og dens symmetriske A'B'C 'fra øvelse 1, sjekk at de tilsvarende sidene til den originale trekanten og dens symmetriske har samme lengde.
Løsning: For å finne avstanden eller lengden på sidene bruker vi den euklidiske avstandsformelen:
d (A, B) = √ ((Bx - Ax) ^ 2 + (By - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
Lengden på den tilsvarende symmetriske siden A'B 'beregnes nedenfor:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
På denne måten bekreftes det at aksial symmetri bevarer avstanden mellom to punkter. Prosedyren kan gjentas for de to andre sidene av trekanten og dens symmetriske for å sjekke invariansen i lengden. For eksempel | AC | = | A'C '| = √5 = 2.236.
Øvelse 3
I forhold til trekanten ABC og dens symmetriske A'B'C 'fra øvelse 1, sjekk at de tilsvarende vinklene til den opprinnelige trekanten og dens symmetriske har samme vinkelmål.
Løsning: For å bestemme målene for vinklene BAC og B'A'C ', skal skalarproduktet til vektorene beregnes først AB med AC og deretter prikkproduktet til A'B ' med A'C '.
Husker at:
A = (2, 5), B = (1, 1) og C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) og C' = (- 3, 3).
Det har:
AB = <1-2, 1-5> Y AC = <3-2, 3-5>
på samme måte
A'B ' = <-1+2, 1-5> Y AC = <-3+2, 3-5>
Deretter blir følgende skalære produkter funnet:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
på samme måte
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
Mål på vinkelen BAC er:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅ |AC |)) =
ArcCos (7 / (4,123⋅2,236)) = 40,6º
Tilsvarende er målingen på vinkelen B'A'C ':
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (|A'B '|⋅ |A'C '|)) =
ArcCos (7 / (4,123⋅2,236)) = 40,6º
Når man konkluderer med at aksial symmetri bevarer vinkelmålet.
Øvelse 4
La være et punkt P av koordinatene (a, b). Finn koordinatene til den aksiale symmetrien P 'i forhold til linjen y = x.
Løsning: Vi vil kalle (a ', b') koordinatene til det symmetriske punktet P 'med hensyn til linjen y = x. Midtpunktet M i segmentet PP 'har koordinater ((a + a') / 2, (b + b ') / 2) og er også på linjen y = x, så følgende likhet er sant:
a + a '= b + b'
På den annen side har segmentet PP 'skråning -1 fordi det er vinkelrett på linjen y = x med skråning 1, slik at følgende likhet gjelder:
b - b '= a' -a
Ved å løse de to foregående likhetene a 'og b' konkluderes det med at:
a '= b og at b' = a.
Det vil si, gitt et punkt P (a, b), er dens aksiale symmetri i forhold til linjen y = x P '(b, a).
Referanser
- Arce M., Blázquez S og andre. Transformasjoner av flyet. Gjenopprettet fra: educutmxli.files.wordpress.com
- Beregning cc. Aksial symmetri. Gjenopprettet fra: calculo.cc
- Superprof. Aksial symmetri. Gjenopprettet fra: superprof.es
- wikipedia. Aksial symmetri. Gjenopprettet fra: es.wikipedia.com
- wikipedia. Sirkulær symmetri. Gjenopprettet fra: en.wikipedia.com
Ingen har kommentert denne artikkelen ennå.