
Tørrstoffer med revolusjonsvolum, typer, løste øvelser
De solid av revolusjon Det er den tredimensjonale figuren som genereres ved å rotere en flat overflate rundt den aksiale aksen eller revolusjonsaksen. Figur 1 viser en animasjon av et solid revolusjon generert på denne måten.
Et annet veldig enkelt å visualisere eksempel består i å generere en høyre sirkulær sylinder, rotere et rektangel med høyde eller lengde h og radius r, rundt den positive x-aksen (figur 2). For å finne volumet er det en kjent formel:
V = areal av base x høyde
Andre faste revolusjoner er sfæren, den rette sirkulære kjeglen og forskjellige figurer, avhengig av overflaten som er satt i rotasjon og selvfølgelig den valgte aksen..
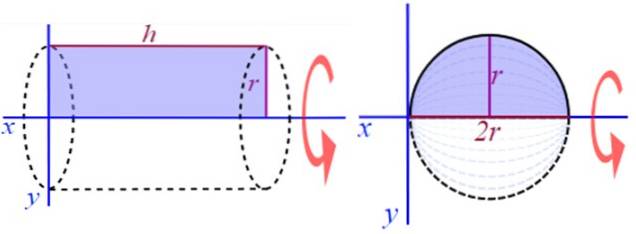
Hvis du for eksempel roterer halvcirkelen rundt en linje parallelt med diameteren, får du et solid hulrull.
For sylinderen, kjeglen, kulen, både solid og hul, er det formler for å finne volumet, som avhenger av radius og høyde. Men når de genereres av andre overflater, beregnes volumet av bestemte integraler.
Artikkelindeks
- 1 Typer av faste revolusjoner
- 1.1 Sfære
- 1.2 Kjegle
- 1.3 Sylinder
- 1.4 Toroid
- 2 Metoder for å beregne volumet av et solid revolusjon
- 2.1 Skive- eller vaskemetode
- 2.2 Lagmetode
- 3 Øvelsen løst
- 4 Referanser
Typer av faste revolusjoner
Tørrstoff i revolusjonen kan klassifiseres i henhold til kurven som genererer dem:
Sfære
Det er nok å rotere en halvcirkel rundt en akse som vil være diameteren på sfæren med radius R. Dens volum er:
Vsfære = (4/3) πR3
Kjegle
For å oppnå en kjegle med høyden H og radius R, er overflaten som skal roteres en rett trekant, rundt den aksiale aksen som går gjennom et av bena. Volumet er:
VKjegle = (1/3) πHRto
Sylinder
Ved å rotere et rektangel rundt en aksial akse som passerer gjennom en av sidene, som kan være kortsiden eller langsiden, får vi en høyre sirkulær sylinder med radius R og høyde H, hvis volum er:
Vsylinder = πRtoH
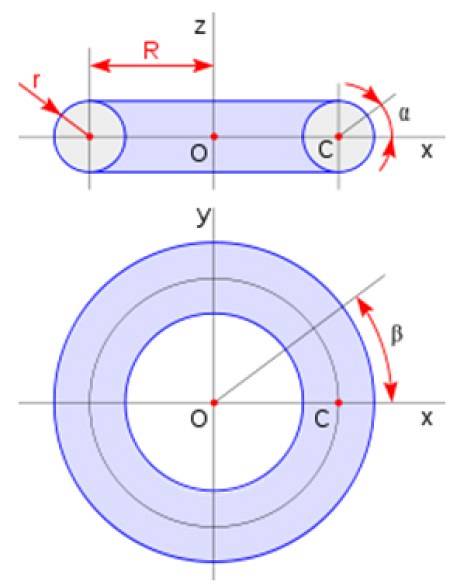
Toroid
Torus er formet som en smultring. Det oppnås ved å rotere et sirkulært område rundt en linje i planet som ikke krysser sirkelen. Volumet er gitt av:
Vtorus = 2πatoR
Hvor a er radiusen til tverrsnittet og R er radiusen til torusen i henhold til skjemaet presentert i figuren:
Metoder for å beregne volumet av et solid revolusjon
I integrert kalkulator er disse to metodene hyppige:
-Skiver og skiver
-Skjell
Skive- eller vaskemetode
Når du skjærer et revolusjonsfast stoff, kan tverrsnittet være en plate, hvis det faste stoffet er solidt, eller det kan være en slags vaskemaskin (en plate med et hull i midten), hvis det er et hul fast stoff..
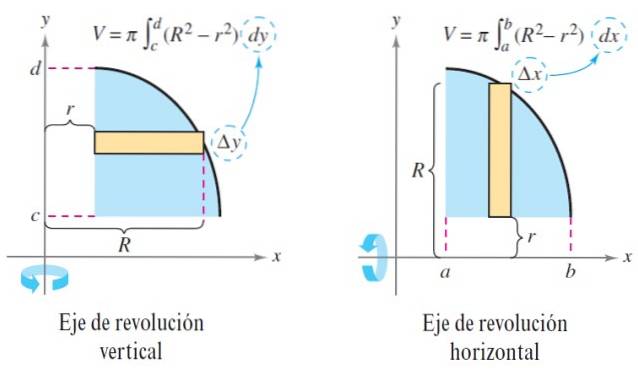
Anta at en plan region roteres rundt den horisontale aksen. Fra dette flate området tar vi et lite rektangel med bredden Δx, som roteres vinkelrett rundt aksialaksen.
Høyden på rektangelet er mellom den ytterste kurven R (x) og den innerste kurven r (x). De tilsvarer henholdsvis den ytre og indre radiusen..
Ved å gjøre denne rotasjonen genereres en vaskemaskin med volum AV, gitt av:
ΔV = Fullt volum - volum av hull (hvis noe)
Husk at volumet til en høyre sirkulær sylinder er π. radioto x høyde, vi har:
AV = π [Rto(x) - rto(x)] Δx
Det faste stoffet kan deles inn i en mengde små volumdeler AV. Hvis vi legger til dem alle, vil vi ha full volum.
For å gjøre dette får vi volumet AV til 0, som Δx også blir veldig lite med, og blir en differensial dx.
Så vi har en integral:
V = ∫tilb π [Rto(x) - rto(x)] dx
Hvis det faste stoffet er solid, er funksjonen r (x) = 0, delen av det faste stoffet som genereres, en disk og volumet forblir:
V = ∫tilb πRto(x) dx
Når revolusjonsaksen er loddrett, får ovenstående ligninger form:
V = ∫tilb π [Rto (y) - rto (y)] dy y V = ∫tilb πRto(y) dy
Lagmetode
Som navnet antyder, består denne metoden i å anta at det faste stoffet består av lag med differensiell tykkelse. Laget er et tynt rør som stammer fra rotasjonen av et rektangel parallelt med rotasjonsaksen.
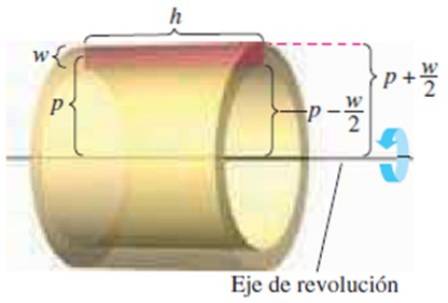
Vi har følgende dimensjoner:
-Høyden på rektangelet w
-Dens lengdegrad h
-Avstanden fra sentrum av rektangelet til rotasjonsaksen s
Å vite at volumet på laget er utvendig volum - innvendig volum:
π (p + w / 2)toh - π (p - w / 2)toh
Ved å utvikle bemerkelsesverdige produkter og forenkle får du:
Lagvolum = 2π⋅p⋅w⋅h
La oss nå lage høyden w på rektangelet Δy, som vist i følgende figur:
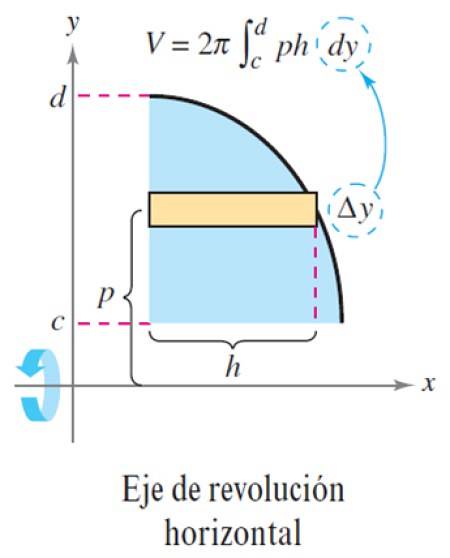
Med dette er volumet AV:
ΔV = 2π p x h x Δy
Og lage antall lag n er veldig stor, Δy blir en differensiell dy, som det totale volumet er integralet med:
V = ∫cd 2π p (y) h (y) dy
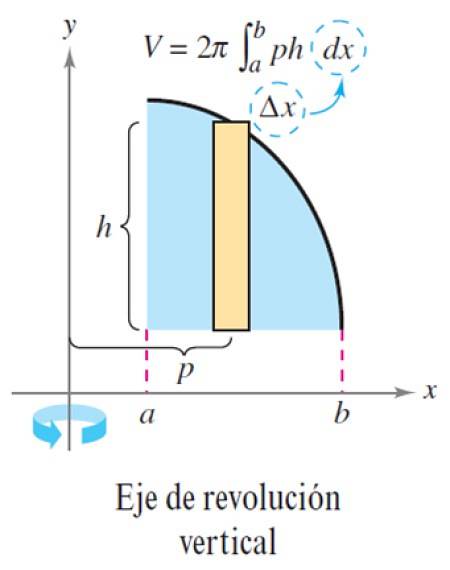
Fremgangsmåten som er beskrevet gjelder på samme måte når revolusjonsaksen er loddrett:
Treningen løst
Finn volumet som genereres av rotasjonen av planområdet mellom kurvene:
y = xto; y = 0; x = 2
Rundt y-aksen.
Løsning
-Det første vi må gjøre er å tegne grafen for regionen som vil generere revolusjonens faststoff og indikere rotasjonsaksen. Vi har det i følgende graf:
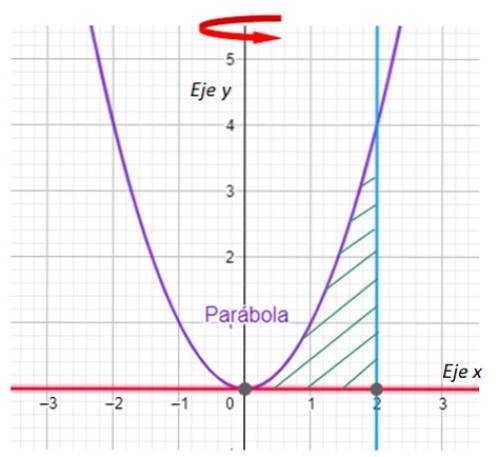
-Nå ser vi etter skjæringspunktene mellom kurven y = xto og linjen x = 2. For sin del er linjen y = 0 ingen ringere enn x-aksen.
Fra grafen er det lett å se at parabolen og linjen krysser hverandre ved punktet (2,4), som bekreftes ved å erstatte x = 2 i y = xto.
-Deretter velges en av metodene for å beregne volumet, for eksempel lagmetoden med vertikal revolusjonsakse:
V = ∫tilb 2π p (x) h (x) dx
Trinn 1: tegne rektangelet
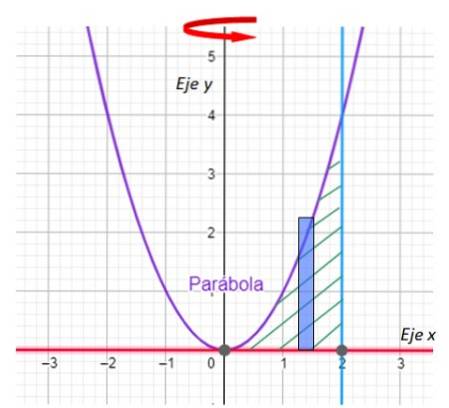
Viktig: I lagdelingsmetoden er langsiden av rektangelet parallelt med rotasjonsaksen.
Trinn 2: Bestem p (x)
Lagets radius er x
Trinn 3: Bestem h (x)
Rektanglets høyde bestemmes av parabolen xto.
Trinn 4: etablere og løse volumintegralen
Integrasjonsvariabelen er x, som varierer mellom 0 og 2, med dette har vi grensene for integrasjon. Erstatte uttrykkene for p (x) og h (x)

Referanser
- Larson, R. 2010. Beregning av en variabel. 9. plass. Utgave. Mcgraw hill.
- Purcell, E. 2007. Kalkulus med analytisk geometri. 9. plass. Utgave. Pearson Education.
- Wikipedia. Solid of Revolution. Gjenopprettet fra: en.wikipedia.org.
- Wikipedia. Toroid Gjenopprettet fra: es.wikipedia.org.
- Wolfram MathWorld. Solid of Revolution. Gjenopprettet fra: mathworld.wolfram.com.


Ingen har kommentert denne artikkelen ennå.