
Eksistens- og unikhetssetningssikkerhet, eksempler og øvelser
De Eksistens- og unikhetssetning etablerer de nødvendige og tilstrekkelige forhold slik at en førsteordens differensialligning, med en gitt starttilstand, har en løsning og at denne løsningen også er den eneste.
Teoremet gir imidlertid ingen teknikk eller indikasjon på hvordan man finner en slik løsning. Eksistens- og unikhetssetningen utvides også til differensialligninger med høyere orden med startbetingelser, som er kjent som Cauchy-problemet..
Den formelle uttalelsen om eksistens- og unikhetssetningen er som følger:
"For en differensialligning y '(x) = f (x, y) med opprinnelig tilstand y (a) = b, eksisterer minst en løsning i et rektangulært område av planet XY inneholder til poenget (a, b), Ja f (x, y) det er kontinuerlig i den regionen. Og hvis delderivatet av F med respekt for Y: g = ∂f / ∂og er kontinuerlig i det samme rektangulære området, så er løsningen unik i nabolaget (a, b) innhold i kontinuitetsregionen av F Y g."
Nytten av denne teoremet ligger først i å vite hvilke regioner i XY-planet en løsning kan eksistere i, og også å vite om løsningen som er funnet er den eneste mulige, eller om det er andre..
Vær oppmerksom på at i tilfelle unikhetsbetingelsen ikke er oppfylt, kan teoremet ikke forutsi hvor mange løsninger totalt Cauchy-problemet har: kanskje det er en, to eller flere.
Artikkelindeks
- 1 Bevis på eksistens- og unikhetssetningen
- 2 Eksempler
- 2.1 - Eksempel 1
- 2.2 - Eksempel 2
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referanser
Bevis på eksistens- og unikhetssetningen

For denne teoremet er to mulige bevis kjent, den ene er beviset for Charles Émile Picard (1856-1941) og den andre skyldes Giuseppe Peano (1858-1932) basert på verkene fra Augustin Louis Cauchy (1789-1857 ).
Det er bemerkelsesverdig at de mest strålende matematiske sinnene i det nittende århundre deltok i beviset på denne teoremet, så det kan være intuitert at ingen av de to er enkle.
For å formelt bevise teoremet, er det nødvendig å først etablere en serie med mer avanserte matematiske begreper, for eksempel funksjoner av Lipschitz-typen, Banach-mellomrom, Carathéodorys eksistenssetning og flere andre, som ligger utenfor artikkelens omfang..
En stor del av differensialligningene som håndteres i fysikk, håndterer kontinuerlige funksjoner i regionene av interesse, derfor vil vi begrense oss til å vise hvordan setningen brukes i enkle ligninger.
Eksempler
- Eksempel 1
La oss vurdere følgende differensialligning med en innledende tilstand:
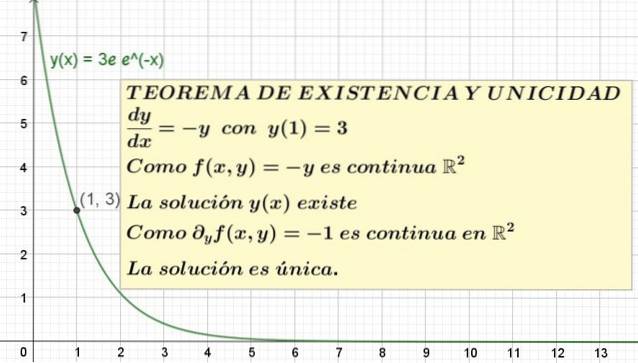
y '(x) = - y; med y (1) = 3
Er det en løsning på dette problemet? Er det den eneste mulige løsningen?
Svar
For det første blir eksistensen av løsningen av differensiallikningen evaluert og at den også oppfyller den opprinnelige betingelsen.
I dette eksemplet f (x, y) = - y eksistensbetingelsen krever å vite om f (x, y) er kontinuerlig i en region av flyet XY som inneholder koordinatpunktet x = 1, y = 3.
Men f (x, y) = - y er den affin funksjon, som er kontinuerlig i domenet til reelle tall og eksisterer i hele reelle tall.
Derfor konkluderes det at f (x, y) er kontinuerlig i Rto, så teoremet garanterer eksistensen av minst én løsning.
Når du vet dette, er det nødvendig å evaluere om løsningen er unik, eller om det tvert imot er mer enn en. For dette er det nødvendig å beregne delderivatet av F med hensyn til variabelen Y:
∂f / ∂y = ∂ (-y) / ∂y = -1
Deretter g (x, y) = -1 som er en konstant funksjon, som også er definert for alle Rto og det er også kontinuerlig der. Det følger at eksistens- og unikhetssatsen garanterer at dette opprinnelige verdiproblemet har en unik løsning, selv om det ikke forteller oss hva det er..
- Eksempel 2
Tenk på følgende ordens ordinære differensialligning med starttilstand:
y '(x) = 2√y; y (0) = 0.
Finnes det en løsning y (x) for dette problemet? I så fall kan du avgjøre om det er en eller flere enn en.
Svar
Vi vurderer funksjonen f (x, y) = 2√y. Funksjonen F er bare definert for y≥0, siden vi vet at et negativt tall mangler en ekte rot. Hva mer f (x, y) er kontinuerlig i øvre halvplan av Rto inkludert X-aksen, så eksistens- og unikhetssatsen garanterer minst en løsning i den regionen.
Nå er startbetingelsen x = 0, y = 0 på kanten av løsningsområdet. Så tar vi delderivatet av f (x, y) med hensyn til y:
∂f/ ∂y = 1 / √y
I dette tilfellet er ikke funksjonen definert for y = 0, akkurat der den opprinnelige tilstanden er.
Hva forteller teoremet oss? Den forteller oss at selv om vi vet at det er minst en løsning, er det øvre halvplanet av X-aksen inkludert X-aksen, siden unikhetsbetingelsen ikke er oppfylt, er det ingen garanti for at det vil være en unik løsning.
Dette betyr at det kan være en eller flere enn en løsning i kontinuitetsområdet til f (x, y). Og som alltid forteller setningen oss ikke hva de kan være.
Løst øvelser
- Øvelse 1
Løs Cauchy-problemet i eksempel 1:
y '(x) = - y; med y (1) = 3.
Finn funksjonen y (x) som tilfredsstiller differensiallikningen og starttilstanden.
Løsning
I eksempel 1 ble det bestemt at dette problemet har en løsning og også er unikt. For å finne løsningen er det første å merke seg at det er en differensialligning av den første graden av skillbare variabler, som skrives som følger:
dy / dx = - y → dy = -y dx
Deling mellom og i begge medlemmer for å skille variablene vi har:
dy / y = - dx
Den ubestemte integralen brukes i begge medlemmer:
∫ (1 / y) dy = - ∫dx
Å løse de ubestemte integralene vi har:
ln (y) = -x + C
hvor C er en konstant integrasjon som bestemmes av den opprinnelige tilstanden:
ln (3) = -1 + C, det vil si C = 1 + ln (3)
Å erstatte verdien av C og omorganisere den gjenstår:
ln (y) - ln (3) = -x + 1
Bruk av følgende logaritmeegenskaper:
Forskjellen på logaritmer er logaritmen til kvotienten
Ovennevnte uttrykk kan skrives slik:
ln (y / 3) = 1 - x
Den eksponensielle funksjonen med base e i begge medlemmer brukes for å oppnå:
y / 3 = e(1 - x)
Som tilsvarer:
y = 3e e-x
Dette er den unike løsningen på ligningen y '= -y med y (1) = 3. Grafen til denne løsningen er vist i figur 1.
- Øvelse 2
Finn to løsninger for problemet i eksempel 2:
y '(x) = 2√ (y); y (0) = 0.
Løsning
Det er også en ligning av skillbare variabler, som, skrevet i differensiell form, ser slik ut:
dy / √ (y) = 2 dx
Å ta den ubestemte integralen i begge medlemmene er fortsatt:
to √ (y) = 2 x + C.
Hvordan vet du at y≥0 i løsningsregionen har vi:
y = (x + C)to
Men siden startbetingelsen x = 0, y = 0 må oppfylles, er konstanten C null og følgende løsning forblir:
y (x) = xto.
Men denne løsningen er ikke unik, funksjonen y (x) = 0 er også en løsning på problemet. Eksistens- og unikhetssetningen som ble brukt på dette problemet i eksempel 2 hadde allerede spådd at det kunne være mer enn én løsning.
Referanser
- Coddington, Earl A.; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill.
- Encyclopedia of Mathematics. Teori for Cauchy-Lipschitz. Gjenopprettet fra: encyclopediaofmath.org
- Lindelöf, Sur l'application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Bind 116, 1894, s. 454-457. Gjenopprettet fra: gallica.bnf.fr.
- Wikipedia. Picards suksessive tilnærmingsmetode. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Setning fra Picard-Lindelöf. Gjenopprettet fra: es.wikipedia.com.
- Zill, D. 1986. Elementære differensiallikninger med applikasjoner. Læresal.



Ingen har kommentert denne artikkelen ennå.