Parabolske skyteegenskaper, formler og ligninger, eksempler

De parabolsk skudd Den består i å kaste et objekt eller prosjektil i en viss vinkel og la det bevege seg under tyngdekraftens virkning. Hvis luftmotstand ikke blir vurdert, vil objektet, uavhengig av natur, følge en parabelbolbane.

Det er en daglig bevegelse, siden blant de mest populære idrettene er de der baller eller baller kastes, enten med hånden, med foten eller med et instrument som for eksempel en racket eller et balltre.

For studien deles parabolskuddet ned i to overlappende bevegelser: en horisontal uten akselerasjon, og den andre vertikal med konstant akselerasjon nedover, som er tyngdekraften. Begge bevegelsene har starthastighet.

La oss si at den horisontale bevegelsen løper langs x-aksen og den vertikale bevegelsen langs y-aksen. Hver av disse bevegelsene er uavhengige av den andre.

Siden det er hovedmål å bestemme posisjonen til prosjektilet, er det nødvendig å velge et passende referansesystem. Detaljer er nedenfor.

Artikkelindeks

• 1 Parabolsk skuddformler og ligninger
  • 1.1 - Bane, maksimal høyde, maksimal tid og horisontal rekkevidde
• 2 Eksempler på parabolskyting
  • 2.1 Parabolskyting i menneskelige aktiviteter
  • 2.2 Det parabolske skuddet i naturen
• 3 Trening
• 4 Referanser

Parabolsk skuddformler og ligninger

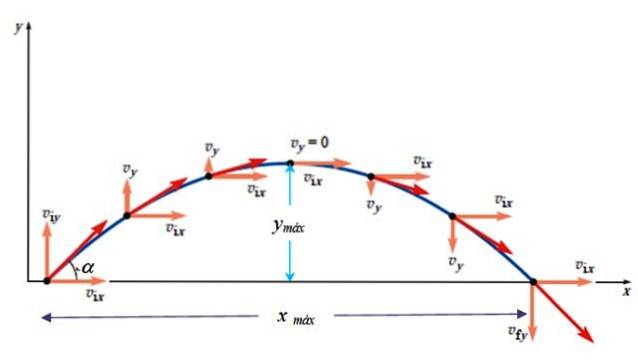
Anta at gjenstanden kastes med vinkel α i forhold til den horisontale og innledende hastigheten v_eller som vist på figuren til venstre. Det parabolske skuddet er en bevegelse som foregår på flyet xy og i så fall brytes utgangshastigheten slik:

v_okse = v_eller cos α

v_Hei = v_eller sin α

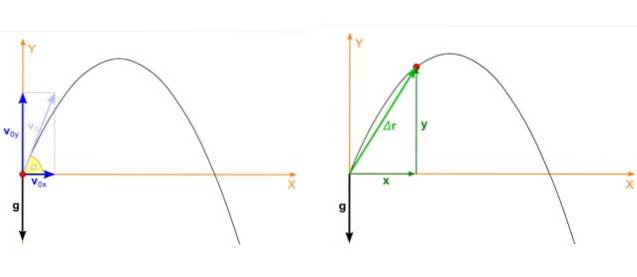
Posisjonen til prosjektilet, som er den røde prikken i figur 2, høyre bilde, har også to tidsavhengige komponenter, en i x og den andre i Y. Posisjon er en vektor betegnet som r og enhetene er lengde.

I figuren sammenfaller prosjektilets utgangsposisjon med opprinnelsen til koordinatsystemet, derfor x_eller = 0, og_eller = 0. Dette er ikke alltid tilfelle, du kan velge opprinnelse hvor som helst, men dette valget forenkler beregningene sterkt.

Når det gjelder de to bevegelsene i x og i y, er disse:

-x (t): er en ensartet rettlinjet bevegelse.

-y (t): tilsvarer en jevnt akselerert rettlinjet bevegelse med g = 9,8 m / s^to og peker loddrett nedover.

I matematisk form:

x (t) = v_eller cos α.t

y (t) = v_eller .sin α.t - ½g.t^to

Posisjonsvektoren er:

r (t) = [v_eller cos α.t]Jeg + [v_eller .sin α.t - ½g.t^to] j

I disse ligningene vil den oppmerksomme leseren legge merke til at minustegnet skyldes tyngdekraften som peker mot bakken, retningen valgt som negativ, mens oppover blir tatt som positiv..

Siden hastighet er det første avledede av posisjon, er det bare å utlede r (t) med hensyn til tid og oppnå:

v (t) = v_eller cos α Jeg + (v_eller .sin α - gt) j

Til slutt uttrykkes akselerasjonen vektorielt som:

til (t) = -g j

- Bane, maksimal høyde, maksimal tid og horisontal rekkevidde

Bane

For å finne den eksplisitte ligningen til banen, som er kurven y (x), må vi eliminere tidsparameteren, løse i ligningen for x (t) og erstatte i y (t). Forenklingen er litt arbeidskrevende, men til slutt får du:

Maksimal høyde

Maksimal høyde oppstår når v_Y = 0. Å vite at det er følgende forhold mellom posisjon og hastighetens kvadrat:

v_Y^to = v_Hei ^to- 2gy

Holder på med v_Y = 0 akkurat når du når maksimal høyde:

0 = v_Hei ^to- 2g. Og_maks → og_maks = v_Hei ^to/ 2 g

Med:

v_Hei = v_eller senα

Maksimal tid

Maksimal tid er den tiden det tar for objektet å nå og_maks. For å beregne det brukes:

v_Y = v_eller .sin α - gt

Vet det v_Y blir 0 når t = t_maks, resultat:

v_eller .sin α - g.t_maks = 0

t_maks = v_Hei / g

Maksimal horisontal rekkevidde og flytid

Rekkevidden er veldig viktig, fordi den signaliserer hvor objektet vil falle. På denne måten vil vi vite om det treffer målet. For å finne den trenger vi flytid, total tid eller t_v.

Fra illustrasjonen ovenfor er det lett å konkludere med det t_v = 2.t_maks. Men vær forsiktig! Dette gjelder bare hvis lanseringen er jevn, det vil si at høyden på startpunktet er den samme som ankomsthøyden. Ellers blir tiden funnet ved å løse den kvadratiske ligningen som er resultatet av å erstatte den endelige posisjonen Y_endelig:

Y_endelig = v_eller .sin α.t_v - ½g.t_v^to

I alle fall er den maksimale horisontale rekkevidden:

x_maks = v_okse. t_v

Eksempler på parabolskyting

Parabolskyting er en del av bevegelsen til mennesker og dyr. Også av nesten alle idretter og spill hvor tyngdekraften griper inn. For eksempel:

Parabolskyting i menneskelige aktiviteter

-Steinen kastet av en katapult.

-Keeperens målspark.

-Ballen kastet av muggen.

-Pilen som kommer ut av baugen.

-Alle slags hopp

-Kast en stein med slynge.

-Ethvert kastet våpen.

Det parabolske skuddet i naturen

-Vann som strømmer fra naturlige eller kunstige stråler som de fra en fontene.

-Steiner og lava strømmer ut av en vulkan.

-En ball som spretter av fortauet eller en stein som spretter på vannet.

-Alle slags hoppende dyr: kenguruer, delfiner, gaseller, katter, frosker, kaniner eller insekter, for å nevne noen.

Trening

En gresshoppe hopper i en vinkel på 55º med den horisontale og lander 0,80 meter foran. Finne:

a) Maksimal høyde nådd.

b) Hvis han hoppet med samme starthastighet, men hadde en vinkel på 45º, ville han da gå høyere??

c) Hva kan sies om maksimal horisontal rekkevidde for denne vinkelen?

Løsning til

Når dataene som leveres av problemet ikke inneholder starthastigheten v_eller beregningene er noe mer arbeidskrevende, men fra de kjente ligningene kan et nytt uttrykk utledes. Starter fra:

x_maks = v_okse . t_flygning = v_eller.cos α. t_v

Når den lander senere, returnerer høyden til 0, så:

v_eller .sin α.t_v - ½g.t_v^to= 0

Hva t_v er en vanlig faktor, er det forenklet:

v_eller .sin α - ½g.t_v= 0

Vi kan fjerne t_v fra første ligning:

t_v = x_maks / v_eller.cos α

Og bytt ut i det andre:

v_eller .sin α - (½g.x_maks / v_eller.cos α) = 0

Ved å multiplisere alle begrepene med v_eller.cos αuttrykket er ikke endret og nevneren forsvinner:

(v_eller .sin α.) (v_eller.cos α) - ½g.x_maks = 0

v_eller^to sin α. cos α = ½g.x_maks

Det kan allerede være ryddet v_eller eller også erstatte følgende identitet:

sin 2α = 2 sin α. cos α → v_eller^to sin 2α = g.x_maks

Er beregnet v_eller^to:

v_eller^to = g.x_maks / sin 2α = (9,8 x 0,8 / sin 110) m^to/ s^to = 8,34 m^to/ s^to

Og til slutt maksimal høyde:

Y_maks= v_Hei ^to/ 2g = (8,34 x sin^to 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Løsning b

Hummeren klarer å opprettholde samme horisontale hastighet, men ved å redusere vinkelen:

Y_maks= v_Hei ^to/ 2g = (8,34 x sin^to 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Nå en lavere høyde.

Løsning c

Maksimal horisontal rekkevidde er:

x_maks = v_eller^to sen 2. / g

Ved å variere vinkelen endres også den horisontale rekkevidden:

x_maks = 8,34 sen 90 / 9.8  m = 0,851 m = 85,1 cm

Hoppet er lenger nå. Leseren kan bekrefte at den er maksimum for 45 ° vinkelen fordi:

sin 2α = sin 90 = 1.

Referanser

1. Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fysikk. Andre utgave. Mcgraw hill.
3. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
4. Resnick, R. 1999. Fysikk. Vol. 1. 3. utgave på spansk. Compañía Editorial Continental S.A. av C.V.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.