
Isometrisk transformasjonssammensetning, typer og eksempler

De isometriske transformasjoner De er endringer i posisjonen eller orienteringen til en bestemt figur som ikke endrer formen eller størrelsen. Disse transformasjonene er klassifisert i tre typer: translasjon, rotasjon og refleksjon (isometri). Generelt lar geometriske transformasjoner deg lage en ny figur fra en gitt.
En transformasjon til en geometrisk figur betyr at den på en eller annen måte har gjennomgått en viss endring; det vil si at den ble endret. I henhold til originalen og lignende i planet kan geometriske transformasjoner klassifiseres i tre typer: isometrisk, isomorf og anamorf..

Artikkelindeks
- 1 Funksjoner
- 2 typer
- 2.1 Ved oversettelse
- 2.2 Ved rotasjon
- 2.3 Ved refleksjon eller symmetri
- 3 Sammensetning
- 3.1 Sammensetning av en oversettelse
- 3.2 Sammensetning av en rotasjon
- 3.3 Sammensetning av en symmetri
- 4 Referanser
Kjennetegn
Isometriske transformasjoner oppstår når størrelsen på segmentene og vinklene mellom den opprinnelige figuren og den transformerte figuren er bevart.
I denne typen transformasjon er verken formen eller størrelsen på figuren endret (de er kongruente), det er bare en endring i posisjonen, enten i retning eller i retning. På denne måten vil de innledende og endelige figurene være like og geometrisk kongruente..
Isometri refererer til likhet; det vil si at geometriske figurer vil være isometriske hvis de har samme form og størrelse.
I isometriske transformasjoner er det eneste som kan observeres en endring av posisjon i planet, en stiv bevegelse oppstår takket være at figuren går fra en startposisjon til en endelig. Denne figuren kalles homolog (lignende) av originalen.
Det er tre typer bevegelser som klassifiserer en isometrisk transformasjon: oversettelse, rotasjon og refleksjon eller symmetri.
Typer
Ved oversettelse
De er de isometriene som gjør at alle punkter i flyet forskyves i en rett linje i en gitt retning og avstand.
Når en figur transformeres ved oversettelse, endrer den ikke sin orientering i forhold til utgangsposisjonen, og den mister heller ikke sine indre mål, målene for vinklene og sidene. Denne typen forskyvning er definert av tre parametere:
- En retning, som kan være horisontal, vertikal eller skrå.
- En sans, som kan være venstre, høyre, opp eller ned.
- Avstand eller størrelse, som er lengden fra utgangsposisjonen til slutten av et punkt som beveger seg.
For at en isometrisk transformasjon ved oversettelse skal oppfylles, må følgende vilkår være oppfylt:
- Figuren må alltid beholde alle dimensjonene, både lineære og vinklede.
- Figuren endrer ikke sin posisjon i forhold til den horisontale aksen; det vil si at vinkelen aldri varierer.
- Oversettelsene vil alltid bli oppsummert i en enkelt, uavhengig av antall oversettelser som blir gjort..
I et plan der sentrum er et punkt O, med koordinater (0,0), er oversettelsen definert av en vektor T (a, b), som indikerer forskyvningen av startpunktet. Nemlig:
P (x, y) + T (a, b) = P '(x + a, y + b)
For eksempel, hvis en oversettelse T (-4, 7) blir brukt på koordinatpunktet P (8, -2), får vi:
P (8, -2) + T (-4, 7) = P '[(8 + (-4)), ((-2) + 7)] = P' (4, 5)
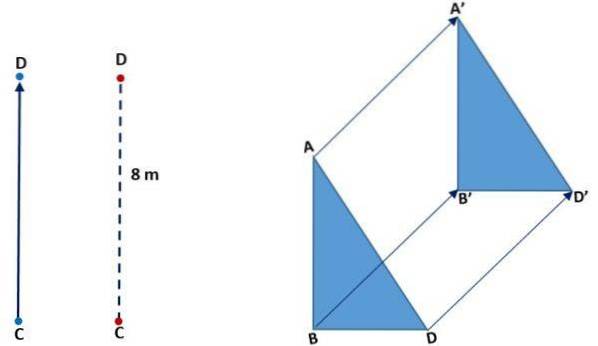
På det følgende bildet (til venstre) kan det sees hvordan punkt C flyttet til å falle sammen med D. Det gjorde det i vertikal retning, retningen var oppover og avstanden eller størrelsen på CD var 8 meter. På høyre bilde observeres oversettelsen av en trekant:
Ved rotasjon
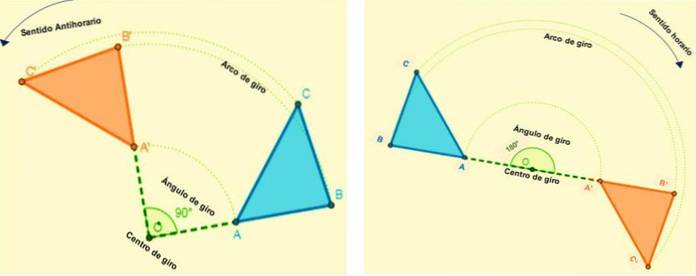
De er de isometriene som lar figuren rotere alle punktene i et plan. Hvert punkt roterer etter en bue som har en konstant vinkel og et fast punkt (rotasjonssenter) bestemt.
Det vil si at all rotasjon vil bli definert av rotasjonssenteret og rotasjonsvinkelen. Når en figur transformeres ved rotasjon, holder den mål på vinkler og sider.
Rotasjonen skjer i en bestemt retning, den er positiv når rotasjonen er mot klokken (mot klokken) og negativ når den er rotert med klokken..
Hvis et punkt (x, y) roteres i forhold til opprinnelsen - det vil si rotasjonssenteret er (0,0) -, med en vinkel på 90eller til 360eller koordinatene til punktene vil være:
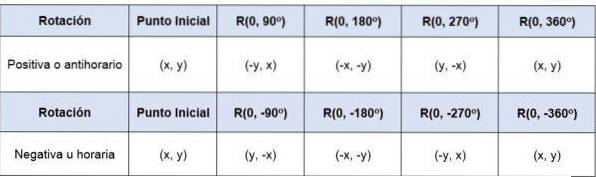
I tilfelle der rotasjonen ikke har et senter ved opprinnelsen, må koordinatsystemets opprinnelse overføres til den nye gitte opprinnelsen, for å kunne rotere figuren med opprinnelsen som sentrum..
For eksempel hvis punktet P (-5,2) roteres 90eller, rundt opprinnelsen og i en positiv retning vil de nye koordinatene være (-2,5).
Ved refleksjon eller symmetri
De er de transformasjonene som inverterer flyets punkter og figurer. Denne inversjonen kan være med hensyn til et punkt, eller det kan også være med hensyn til en linje.
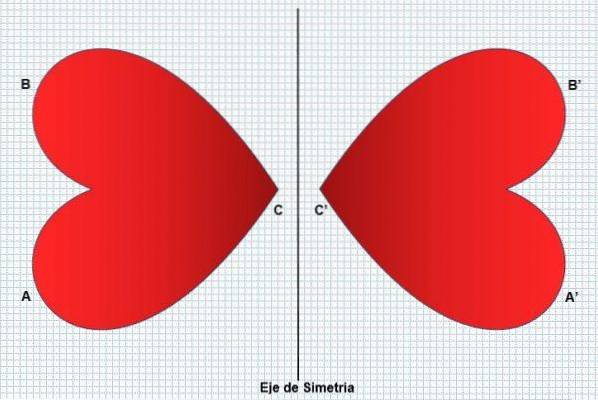
Med andre ord, i denne typen transformasjon er hvert punkt i den opprinnelige figuren assosiert med et annet punkt (bilde) av den homologe figuren, på en slik måte at punktet og dets bilde er i samme avstand fra en linje som kalles aksen av symmetri..
Dermed vil den venstre delen av figuren være en refleksjon av den høyre delen, uten å endre form eller dimensjoner. Symmetri forvandler en figur til en annen lik, men i motsatt retning, som det fremgår av følgende bilde:
Symmetri er til stede i mange aspekter, for eksempel i noen planter (solsikker), dyr (påfugl) og naturfenomener (snøflak). Mennesket reflekterer det i ansiktet, som regnes som en skjønnhetsfaktor. Refleksjon eller symmetri kan være av to typer:
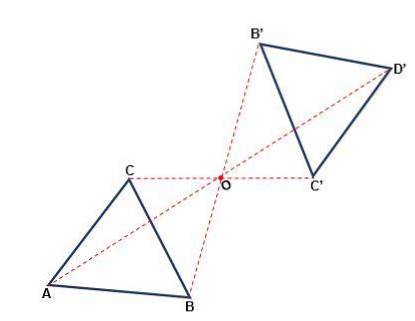
Sentral symmetri
Det er den transformasjonen som skjer med hensyn til et punkt der figuren kan endre sin orientering. Hvert punkt i den opprinnelige figuren og bildet har samme avstand fra et punkt O, kalt sentrum for symmetri. Symmetri er sentral når:
- Både poenget og dets bilde og sentrum tilhører samme linje.
- Med en rotasjon på 180eller fra sentrum O oppnås en figur lik originalen.
- Slagene til den opprinnelige figuren er parallelle med slagene til den dannede figuren.
- Følelsen av figuren endres ikke, den vil alltid være med klokken.
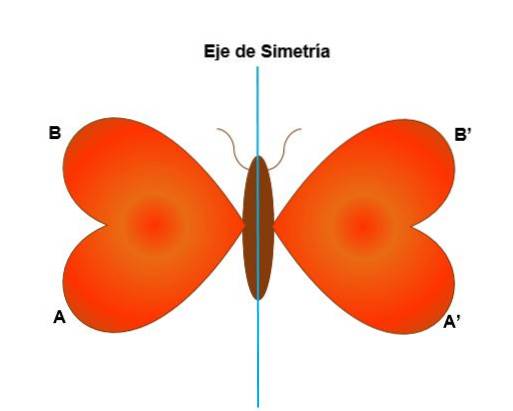
Denne transformasjonen skjer med hensyn til symmetriaksen, hvor hvert punkt i den opprinnelige figuren er assosiert med et annet punkt i bildet, og disse er i samme avstand fra symmetriaksen. Symmetri er aksial når:
- Segmentet som forbinder et punkt med bildet, er vinkelrett på symmetriaksen.
- Figurene endrer retning i forhold til rotasjon eller med urviseren.
- Når du deler figuren med en sentral linje (symmetriakse), faller en av de resulterende halvdelene helt sammen med en annen av halvdelene.
Sammensetning
En sammensetning av isometriske transformasjoner refererer til suksessiv anvendelse av isometriske transformasjoner på samme figur.
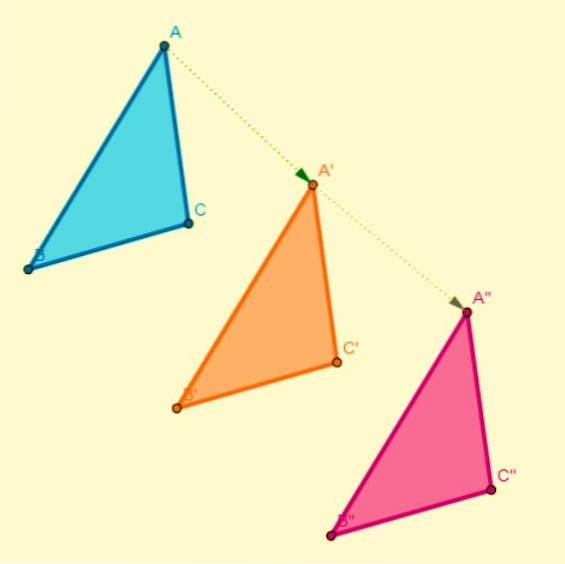
Sammensetning av en oversettelse
Sammensetningen av to oversettelser resulterer i en annen oversettelse. Når den utføres på flyet, endres bare koordinatene til den aksen på den horisontale aksen (x), mens koordinatene til den vertikale aksen (y) forblir de samme, og omvendt.
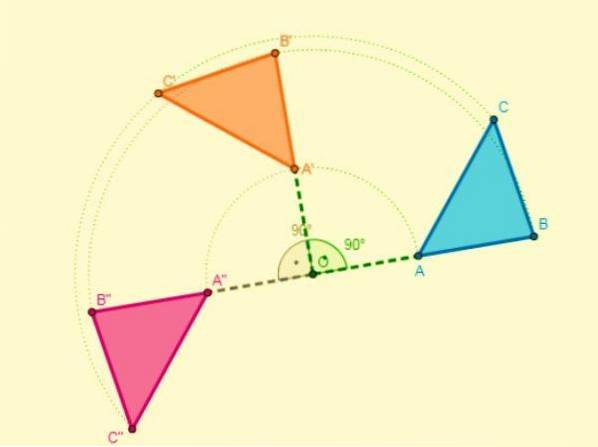
Sammensetning av en rotasjon
Sammensetningen av to svinger med samme senter resulterer i en annen sving, som har samme sentrum og hvis amplitude vil være summen av amplitudene til de to svingene..
Hvis midten av svingene har et annet senter, vil snittet på halveringen av to segmenter av lignende punkter være sentrum for svingen.
Sammensetning av en symmetri
I dette tilfellet vil sammensetningen avhenge av hvordan den brukes:
- Hvis den samme symmetrien blir brukt to ganger, blir resultatet en identitet.
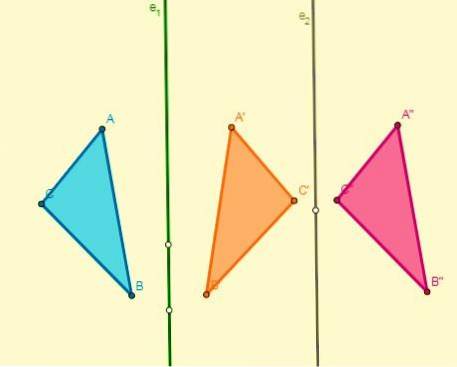
- Hvis to symmetrier brukes på to parallelle akser, blir resultatet en oversettelse, og forskyvningen er dobbelt så langt fra aksene:
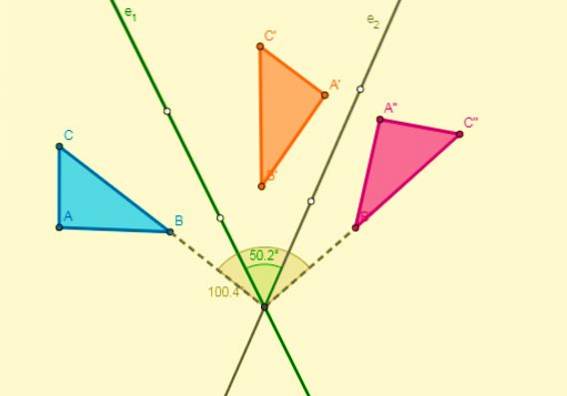
- Hvis to symmetrier brukes med hensyn til to akser som krysser ved punkt O (sentrum), vil en rotasjon med sentrum ved O bli oppnådd, og vinkelen vil være dobbelt så stor som vinkelen dannet av aksene:
Referanser
- V Burgués, J. F. (1988). Materialer for konstruksjon av geometri. Madrid: Syntese.
- Cesar Calavera, I. J. (2013). Teknisk tegning II. Paraninfo S.A: Editions of the Tower.
- Coxeter, H. (1971). Grunnleggende om geometri. Mexico: Limusa-Wiley.
- Coxford, A. (1971). Geometri En transformasjonsmetode. USA: Laidlaw Brothers.
- Liliana Siñeriz, R. S. (2005). Induksjon og formalisering i undervisningen av stive transformasjoner i CABRI-miljøet.
- , P. J. (1996). Gruppen av isometrier til flyet. Madrid: Syntese.
- Suárez, A. C. (2010). Transformasjoner i flyet. Gurabo, Puerto Rico: AMCT .



Ingen har kommentert denne artikkelen ennå.