Ovale (geometriske figur) egenskaper, eksempler, øvelser

De oval symmetrisk er definert som en flat og lukket kurve, som har to vinkelrette symmetriakser-en dur og en mindre- og består av to omkretsbuer like to og to.

På denne måten kan det tegnes ved hjelp av et kompass og noen referansepunkter på en av linjene for symmetri. I alle fall er det flere måter å tegne det, som vi vil se senere.

Det er en veldig kjent kurve, siden den er anerkjent som konturen til en ellips, dette er et spesielt tilfelle av den ovale. Men den ovale er ikke en ellipse, selv om den noen ganger ser veldig ut som den, siden dens egenskaper og utforming er forskjellige. For eksempel er ellipsen ikke konstruert med et kompass.

Artikkelindeks

• 1 Funksjoner
• 2 Eksempler
  • 2.1 Konstruksjon av en oval ved bruk av konsentriske sirkler
• 3 Øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referanser

Kjennetegn

Den ovale har svært varierte bruksområder: arkitektur, industri, grafisk design, urmakeri og smykker er bare noen områder der bruken skiller seg ut..

De mest fremragende egenskapene til denne viktige kurven er følgende:

-Den tilhører gruppen av tekniske kurver: den tegnes ved å danne omkretsbuer ved hjelp av et kompass.

-Alle punktene er på samme plan.

-Mangler kurver eller løkker.

-Oppsettet er kontinuerlig.

-Kurven til den ovale skal være glatt og konveks.

-Når du tegner en linje som tangerer det ovale, er det hele på samme side av linjen.

-En oval innrømmer bare to tangenter parallelt på det meste.

Eksempler

Det er flere metoder for å konstruere ovaler som krever bruk av linjal, firkant og kompass. Så skal vi nevne noen av de mest brukte.

Konstruksjon av en oval ved bruk av konsentriske sirkler

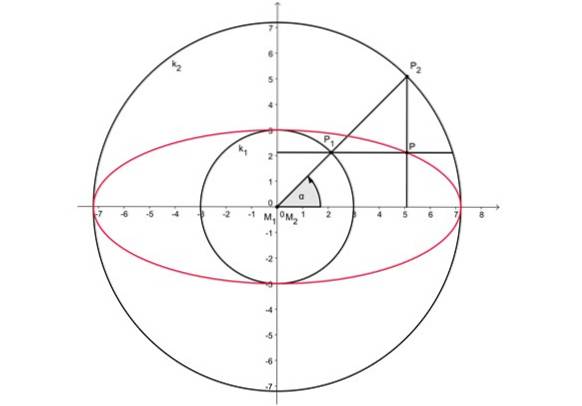
Figur 2 over viser to konsentriske sirkler sentrert ved opprinnelsen. Hovedaksen til den ovale måler den samme som diameteren på den ytre omkretsen, mens den mindre aksen tilsvarer diameteren på den indre omkretsen.

-En vilkårlig radius trekkes til den ytre omkretsen, som krysser begge sirkler ved punktene P₁ Og s_to.

-Deretter projiseres punkt P_to på den horisontale aksen.

-Tilsvarende er punktet P projisert₁ på den vertikale aksen.

-Krysset mellom begge projeksjonslinjene er punkt P og tilhører det ovale.

-Alle punktene i denne delen av det ovale kan plottes på denne måten.

-Resten av det ovale spores med den analoge prosedyren, utført i hver kvadrant.

Opplæring

Deretter vil andre måter å konstruere ovaler undersøkes, gitt en viss innledende måling, som vil bestemme størrelsen..

- Øvelse 1

Tegn ved hjelp av en linjal og et kompass en oval, kjent som dens hovedakse, hvis lengde er 9 cm.

Løsning

I figur 3, vist nedenfor, vises den resulterende ovalen i rødt. Spesiell oppmerksomhet må rettes mot de stiplede linjene, som er hjelpekonstruksjonene som er nødvendige for å tegne en oval hvis hovedakse er spesifisert. Vi skal indikere alle nødvendige trinn for å nå den endelige tegningen.

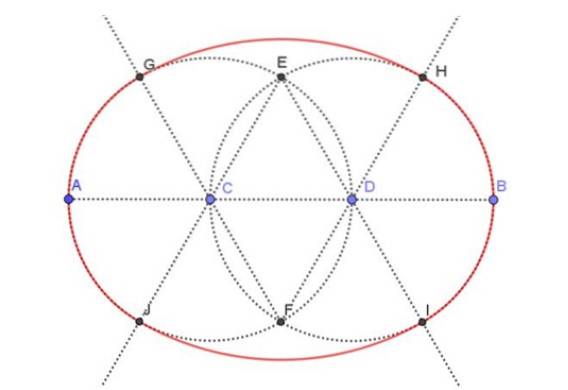
Trinn 1

Tegn med linjal segmentet AB på 9 cm.

Steg 2

Trisect segment AB, det vil si dele det opp i tre like lange segmenter. Siden det originale segmentet AB er 9 cm, må segmentene AC, CD og DB måle hver 3 cm.

Trinn 3

Med kompasset, sentrert ved C og åpning CA, tegnes en ekstra omkrets. Tilsvarende er tilleggsomkretsen med sentrum D og radius DB tegnet med kompasset..

Trinn 4

Kryssene til de to hjelpesirklene som ble bygget i forrige trinn er markert. Vi kaller det punkt E og F.

Trinn 5

Med regelen tegnes følgende stråler: [FC], [FD), [EC], [ED].

Trinn 6

Strålene fra forrige trinn skjærer de to hjelpesirklene på henholdsvis punktene G, H, I, J.

Trinn 7

Med kompasset er laget i F og med åpning (eller radius) FG tegnes buen GH. På samme måte, sentrert ved E og radius EI, tegnes buen IJ.

Trinn 8

Foreningen av buene GJ, JI, IH Y HG danner en oval med hovedaksen er 9 cm.

Trinn 9

Vi fortsetter med å slette (skjule) hjelpepunktene og linjene.

- Øvelse 2

Tegn en oval med linjal og kompass, hvis mindre akse er kjent og dens mål er 6 cm.

Løsning

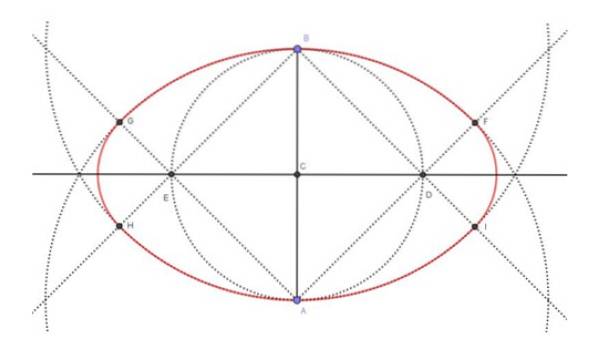
Figuren over (figur 4) viser det endelige resultatet av konstruksjonen av den ovale (i rødt), samt de mellomliggende konstruksjonene som er nødvendige for å nå den. Trinnene som ble fulgt for å bygge den 6 cm ovalen med mindre akse var som følger:

Trinn 1

Det 6 cm lange segmentet AB spores med linjalen.

Steg 2

Med kompasset og linjalen blir halveringen sporet til segment AB.

Trinn 3

Krysset mellom halveringslinjen og segmentet AB resulterer i midtpunktet C for segmentet AB.

Trinn 4

Med kompasset tegnes omkretsen av sentrum C og radius CA.

Trinn 5

Omkretsen som er tegnet i forrige trinn skjærer tverrsnittet av AB ved punktene E og D..

Trinn 6

Strålene [AD], [AE), [BD) og [BE) er tegnet.

Trinn 7

Med kompasset tegnes omkretsene til sentrum A og radius AB og sentrum B og radius BA..

Trinn 8

Skjæringspunktene mellom sirklene tegnet i trinn 7, og strålene konstruert i trinn 6, bestemmer fire punkter, nemlig: F, G, H, I.

Trinn 9

Med sentrum ved D og radius DI tegnes buen IF. På samme måte, med sentrum i E og radius EG, tegnes buen GH.

Trinn 10

Foreningen av omkretsbuer FG, GH, HI og IF bestemmer ønsket oval.

Referanser

1. Ed Plastic. Tekniske kurver: ovaler, ovoider og spiraler. Gjenopprettet fra: drajonavarres.wordpress.com.
2. Mathematische Basteleien. Eggkurver og ovaler. Gjenopprettet fra: mathematische-basteleien.
3. Universitetet i Valencia. Kjegler og flate tekniske kurver. Gjenopprettet fra: ocw.uv.es.
4. Wikipedia. Oval. Gjenopprettet fra: es.wikipedia.org.
5. Wikipedia. Oval. Gjenopprettet fra: en.wikipedia.org.