
Normal vektorberegning og eksempel
De normal vektor er den som definerer retningen vinkelrett på noen geometrisk enhet under vurdering, som for eksempel kan være en kurve, et plan eller en overflate.
Det er et veldig nyttig konsept i posisjonering av en bevegelig partikkel eller en eller annen overflate i rommet. I den følgende grafen er det mulig å se hvordan den normale vektoren til en vilkårlig kurve er C:
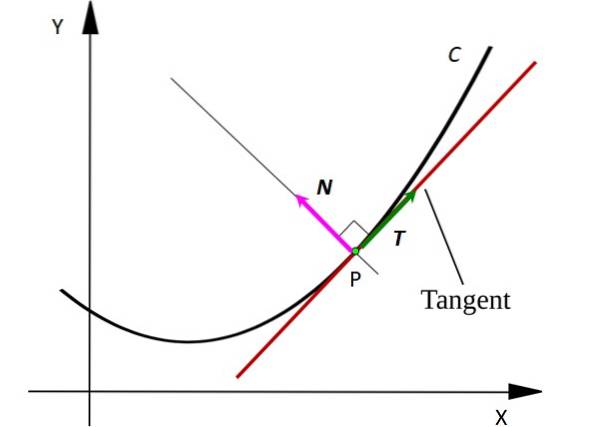
Tenk på et punkt P på kurven C. Punktet kan representere en bevegelig partikkel som beveger seg langs en C-formet bane. Tangenslinjen til kurven ved punkt P er tegnet i rødt..
Legg merke til at vektoren T er tangent til C på hvert punkt, mens vektoren N er vinkelrett på T y peker på midten av en imaginær sirkel hvis bue er et segment av C. Vektorer er angitt med fet skrift i trykt tekst, for å skille dem fra andre ikke-vektorstørrelser.
Vektoren T det indikerer alltid hvor partikkelen beveger seg, derfor indikerer den hastigheten. I stedet for vektoren N peker alltid i retningen der partikkelen roterer, på denne måten indikerer den konkaviteten til kurven C.
Artikkelindeks
- 1 Hvordan få normalvektoren til et plan?
- 1.1 Den normale vektoren fra vektorproduktet
- 2 Eksempel
- 2.1 Løsning
- 2.2 Beregning av vektorproduktet AB x AC
- 3 Referanser
Hvordan få den normale vektoren til et plan?
Den normale vektoren er ikke nødvendigvis en enhetsvektor, det vil si en vektor hvis modul er 1, men i så fall kalles den normal enhetsvektor.
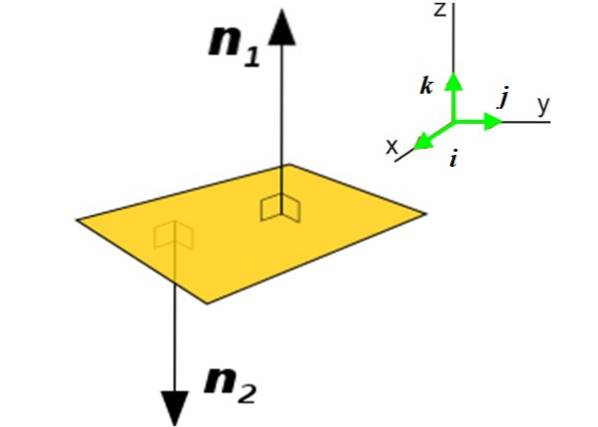
I mange applikasjoner er det nødvendig å kjenne den normale vektoren til et plan i stedet for en kurve. Denne vektoren avslører orienteringen av planet i rommet. Tenk for eksempel på flyet P (gul) av figuren:
Det er to normale vektorer til dette planet: n1 Y nto. Bruken av det ene eller det andre vil avhenge av konteksten der planet er funnet. Å skaffe normalvektoren til et plan er veldig enkelt hvis du vet ligningen:
ax + av + cz + d = 0, med til, b, c Y d reelle tall.
Vel, en normal vektor til nevnte plan er gitt av:
N = a Jeg + b j + c k
Her vektoren N Det uttrykkes i form av enhetsvektorene og vinkelrett på hverandre Jeg, j Y k, rettet langs de tre retningene som bestemmer rommet X og Z, se figur 2 til høyre.
Den normale vektoren fra vektorproduktet
En veldig enkel prosedyre for å finne den normale vektoren bruker egenskapene til vektorproduktet mellom to vektorer.
Som kjent er det tre forskjellige punkter, og som ikke kollinerer med hverandre, bestemmer et plan P. Nå er det mulig å oppnå to vektorer eller Y v som hører til nevnte fly som har disse tre punktene.
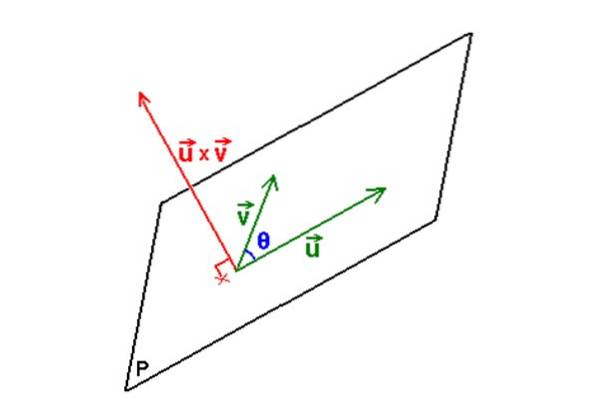
Når du har vektorene, vil vektor produkt eller x v er en operasjon hvis resultat i sin tur er en vektor, som har egenskapen til å være vinkelrett på planet bestemt av eller Y v.
Kjent denne vektoren, er den betegnet som N, og fra det vil det være mulig å bestemme ligningen til planet takket være ligningen som er angitt i forrige avsnitt:
N = eller x v
Følgende figur illustrerer fremgangsmåten som er beskrevet:
Eksempel
Finn ligningen til planet bestemt av punktene A (2,1,3); B (0,1,1); C (4,2,1).
Løsning
Denne øvelsen illustrerer fremgangsmåten beskrevet ovenfor. Ved å ha 3 poeng blir en av dem valgt som den felles opprinnelsen til to vektorer som tilhører planet definert av disse punktene. For eksempel er punkt A satt som opprinnelse og vektorene er konstruert AB Y AC.
Vektoren AB er vektoren der opprinnelsen er punkt A og hvis endepunkt er punkt B. Koordinatene til vektoren AB bestemmes ved å trekke koordinatene til B fra koordinatene til A henholdsvis:
AB = (0-2) Jeg + (1-1) j + (1-3) k = -2Jeg + 0j -to k
Vi fortsetter på samme måte for å finne vektoren AC:
AC = (4-2) Jeg + (2-1) j + (1-3) k = 2Jeg + j -to k
Beregning av vektorproduktet AB x AC
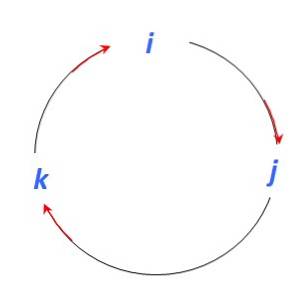
Det er flere prosedyrer for å finne vektorproduktet mellom to vektorer. Dette eksemplet bruker en mnemonisk prosedyre som bruker følgende figur for å finne vektorproduktene mellom enhetsvektorene Jeg, j Y k:
Til å begynne med er det godt å huske at vektorproduktene mellom parallelle vektorer er null, derfor:
Jeg x Jeg = 0; j x j = 0; k x k = 0
Og siden vektorproduktet er en annen vektor vinkelrett på de vektorene som deltar, når vi beveger oss i retning av den røde pilen har vi:
Jeg x j = k ; j x k = Jeg; k x Jeg = j
Hvis du må bevege deg i motsatt retning av pilen, så legg til et tegn (-):
j x Jeg = - k; k x j = -Jeg; Jeg x k = -j
Totalt er det mulig å lage 9 vektorprodukter med enhetsvektorene Jeg, j Y k, hvorav 3 vil være null.
AB x AC = (-2Jeg + 0j -to k) x (2Jeg + j -to k) = -4 (Jeg x Jeg) to (Jeg x j) +4 (Jeg x k) +0 (j x Jeg) + 0 (j x j) - 0 (j x k) - 4 (k x Jeg) to (k x j) + 4 (k x k) = -2k-4j-4j+toJeg = 2Jeg -8j-tok
Ligningen til flyet
Vektoren N er bestemt av vektorproduktet som er beregnet tidligere:
N = toJeg -8j-tok
Derfor er a = 2, b = -8, c = -2, det søkte planet er:
ax + av + cz + d = 0 → 2x-8y-2z + d = 0
Verdien av d. Dette er enkelt hvis verdiene til noen av punktene A, B eller C som er tilgjengelige er erstattet i ligningen av planet. Velge C for eksempel:
x = 4; y = 2; z = 1
Rester:
2,4 - 8,2 - 2,1 + d = 0
-10 + d = 0
d = 10
Kort sagt er det søkte kartet:
2x-8y-2z +10 = 0
Den nysgjerrige leseren lurer kanskje på om det samme resultatet hadde blitt oppnådd hvis i stedet for å gjøre AB x AC de ville ha valgt å gjennomføre AC x AB. Svaret er ja, planet bestemt av disse tre punktene er unikt og har to normale vektorer, som vist i figur 2.
Når det gjelder punktet valgt som opprinnelsen til vektorene, er det ikke noe problem å velge noen av de to andre.
Referanser
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB). 31-62.
- Finne det normale til et fly. Gjenopprettet fra: web.ma.utexas.edu.
- Larson, R. (1986). Kalkulus og analytisk geometri. Mc Graw Hill. 616 - 647.
- Linjer og fly i R 3. Gjenopprettet fra: math.harvard.edu.
- Normal vektor. Gjenopprettet fra mathworld.wolfram.com.



Ingen har kommentert denne artikkelen ennå.