
Vinkelhastighetsdefinisjon, formel, beregning og øvelser
De vinkelhastighet er et mål på rotasjonshastigheten og er definert som vinkelen som posisjonsvektoren til det roterende objektet roterer, per tidsenhet. Det er en størrelse som veldig godt beskriver bevegelsen til et mangfold av objekter som stadig roterer overalt: CDer, bilhjul, maskiner, jorden og mange flere..
Et diagram av "London eye" kan sees i følgende figur. Den representerer bevegelsen til en passasjer representert ved punkt P, som følger den sirkulære banen, kalt c:
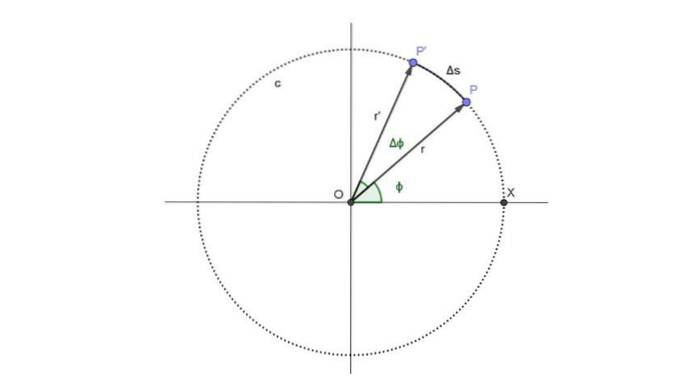
Passasjeren inntar posisjon P i øyeblikkelig t og vinkelposisjonen som tilsvarer det øyeblikket er ϕ.
Fra øyeblikket t går en periode Δt. I denne perioden er den punktuelle passasjerens nye posisjon P 'og vinkelposisjonen har økt med en vinkel Δϕ.
Artikkelindeks
- 1 Hvordan beregner du vinkelhastigheten ?
- 1.1 Forholdet mellom lineær og vinkelhastighet
- 2 Ensartet rotasjonsbevegelse
- 3 Løste problemer med vinkelhastighet
- 3.1 Øvelse 1
- 4 Øvelse 2
- 4.1 Øvelse 3
- 4.2 Øvelse 4
- 5 Referanser
Hvordan beregner du vinkelhastigheten ?
For rotasjonsmengder brukes greske bokstaver mye for å skille dem fra lineære størrelser. Så først definerer vi den gjennomsnittlige vinkelhastigheten ωm som vinkelen reiste i en gitt tidsperiode.
Da vil kvosienten Δϕ / Δt representere den gjennomsnittlige vinkelhastigheten ωm mellom tidene t og t + Δt.
Hvis du vil beregne vinkelhastighet akkurat i øyeblikket t, så må vi beregne kvotienten Δϕ / Δt når Δt ➡0:

Forholdet mellom lineær og vinkelhastighet
Lineær hastighet v, er kvotienten mellom den tilbakelagte avstanden og tiden det tar å reise den.
I figuren over er buen som er reist Δs. Men den buen er proporsjonal med den tilbakelagte vinkelen og radiusen, og følgende forhold oppfylles, som er gyldig så lenge Δϕ måles i radianer:
Δs = r ・ Δϕ
Hvis vi deler det forrige uttrykket med tidsforløpet Δt og tar grensen når Δt ➡0, får vi:
v = r ・ ω
Ensartet rotasjonsbevegelse

En rotasjonsbevegelse er ensartet hvis vinkelen som er reist på et hvilket som helst observert øyeblikk er den samme i samme tidsperiode.
Hvis rotasjonen er jevn, faller vinkelhastigheten når som helst sammen med den gjennomsnittlige vinkelhastigheten.

Videre, når en fullstendig sving er gjort, er den tilbakelagte vinkelen 2π (tilsvarende 360º). Derfor, i en jevn rotasjon, er vinkelhastigheten related relatert til perioden T, med følgende formel:

f = 1 / T
Med andre ord, i en jevn rotasjon, er vinkelhastigheten relatert til frekvensen ved:
ω = 2π ・ f
Løste problemer med vinkelhastighet
Øvelse 1
Førerhusene til det store snurrhjulet, kjent som "London Eye”De beveger seg sakte. Fart på førerhusene er 26 cm / s og hjulet er 135 m i diameter.
Beregn med disse dataene:
i) Hjulets vinkelhastighet
ii) Rotasjonsfrekvensen
iii) Tiden det tar for en hytte å gjøre en hel sving.
Svar:
Jeg) Hastigheten v i m / s er: v = 26 cm / s = 0,26 m / s.
Radien er halve diameteren: r = (135 m) / 2 = 67,5 m
v = r ・ ω => ω = v / r = (0,26 m / s) / (67,5 m) = 0,00385 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10-4 svinger / s
f = 6,13 x 10 ^ -4 omdreining / s = 0,0368 omdreining / min = 2,21 omdreining / time.
iii) T = 1 / f = 1 / 2,21 runde / time = 0,45311 time = 27 min 11 sek
Øvelse 2
En lekebil beveger seg på et sirkulært spor med en radius på 2m. Ved 0 s er vinkelposisjonen 0 rad, men etter en tid t blir vinkelposisjonen gitt av:
φ (t) = 2 ・ t
Fastslå:
i) Vinkelhastigheten
ii) Den lineære hastigheten når som helst.
Svar:
Jeg) Vinkelhastigheten er avledet av vinkelposisjonen: ω = φ '(t) = 2.
Det vil si at lekebilen til enhver tid har konstant vinkelhastighet lik 2 rad / s.
ii) Den lineære hastigheten til bilen er: v = r ・ ω = 2 m ・ 2 rad / s = 4 m / s = 14,4 Km / h
Øvelse 3
Den samme bilen fra forrige øvelse begynner å stoppe. Dens vinkelposisjon som en funksjon av tid er gitt av følgende uttrykk:
φ (t) = 2 ・ t - 0,5 ・ tto
Fastslå:
i) Vinkelhastigheten når som helst
ii) Den lineære hastigheten når som helst
iii) Tiden det tar å stoppe fra det øyeblikket det begynner å avta
iv) Vinkelen som er reist
v) tilbakelagt avstand
Svar:
Jeg) Vinkelhastigheten er avledet av vinkelposisjonen: ω = φ '(t)
ω (t) = φ '(t) = (2 ・ t - 0,5 ・ tto) '= 2 - t
ii) Den lineære hastigheten til bilen når som helst er gitt av:
v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t
iii) Tiden det tar å stoppe fra det øyeblikket den begynner å bremse, bestemmes ved å kjenne øyeblikket hvor hastigheten v (t) blir null.
v (t) = 4 - 2 t = 0 => t = 2
Det vil si at den stopper 2 s etter å ha startet å bremse.
iv) I perioden 2s fra den begynner å bremse til den stopper, beveges en vinkel gitt av φ (2):
φ (2) = 2 ・ 2 - 0,5 ・ 2 ^ 2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 grader
v) I perioden 2 s fra den begynner å bremse til den stopper, er en avstand s gitt av:
s = r ・ φ = 2m ・ 2 rad = 4 m
Øvelse 4
Hjulene på en bil er 80 cm i diameter. Hvis bilen kjører i 100 km / t. Finn: i) hjulens rotasjonshastighet, ii) hjulens rotasjonsfrekvens, iii) Antall omdreininger hjulet gjør i løpet av en time.
Svar:
Jeg) Først skal vi konvertere hastigheten på bilen fra Km / t til m / s
v = 100 km / t = (100 / 3,6) m / s = 27,78 m / s
Hjulens rotasjonshastighet er gitt av:
ω = v / r = (27,78 m / s) / (0,4 m) = 69,44 rad / s
ii) Hjulens rotasjonsfrekvens er gitt av:
f = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 omdreining / s
Rotasjonsfrekvensen uttrykkes vanligvis i omdreininger per minutt omdr./min.
f = 11.05 omdreining / s = 11.05 omdreining / (1/60) min = 663.15 omdr./min
iii) Antall runder hjulet tar i løpet av en times reise beregnes vel vitende om at 1 time = 60 min, og at frekvensen er antall runder N delt på tiden da N runder blir laget.
f = N / t => N = f ・ t = 663,15 (svinger / min) x 60 min = 39788,7 svinger.
Referanser
- Giancoli, D. Fysikk. Prinsipper med applikasjoner. 6. utgave. Prentice Hall. 106-108.
- Resnick, R. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 67-69.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Utgave. Mexico. Cengage Learning Editors. 84-85.
- geogebra.org



Ingen har kommentert denne artikkelen ennå.