
Gjennomsnittlig vinkelhastighetsdefinisjon og formler, løste øvelser
De gjennomsnittlig vinkelhastighet Rotasjon er definert som vinkelen rotert per tidsenhet for posisjonsvektoren til et punkt som beskriver sirkelbevegelse. Bladene til en takvifte (som den som er vist i figur 1), følger sirkelbevegelse og deres gjennomsnittlige vinkelhastighet beregnes ved å ta kvotienten mellom den roterte vinkelen og tiden den vinkelen ble kjørt på..
Reglene som rotasjonsbevegelse følger er noe lik de kjente for translasjonsbevegelse. De tilbakelagte avstandene kan også måles i meter, men vinkelstørrelsene får spesiell relevans fordi de i stor grad letter beskrivelsen av bevegelsen.
Generelt brukes greske bokstaver for vinkelmengdene og latinske bokstaver for de tilsvarende lineære størrelsene..
Artikkelindeks
- 1 Definisjon og formler
- 1.1 Ensartet rotasjon
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 3 Referanser
Definisjon og formler
Figur 2 representerer bevegelsen til et punkt på en sirkelbane c. Posisjonen P for punktet tilsvarer øyeblikket t og vinkelposisjonen som tilsvarer det øyeblikket er ϕ.
Fra øyeblikket t går en periode Δt. I den perioden er punktets nye posisjon P ', og vinkelposisjonen har økt med en vinkel A.
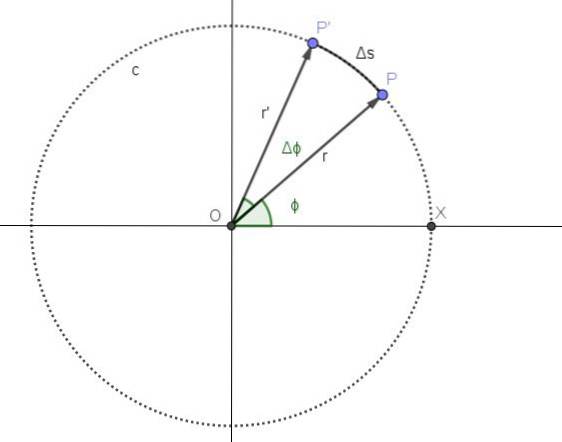
Gjennomsnittlig vinkelhastighet ω er vinkelen som er reist per tidsenhet, slik at kvotienten Δϕ / Δt vil representere den gjennomsnittlige vinkelhastigheten mellom tidene t og t + Δt:
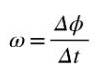
Siden vinkel måles i radianer og tid i sekunder, er enheten for gjennomsnittlig vinkelhastighet rad / s. Hvis du vil beregne vinkelhastighet akkurat i øyeblikket t, så må vi beregne kvotienten Δϕ / Δt når Δt ➡0.

Jevn rotasjon
En rotasjonsbevegelse er ensartet hvis vinkelen som er reist til enhver tid er den samme i samme tidsperiode. Hvis rotasjonen er jevn, faller vinkelhastigheten når som helst sammen med den gjennomsnittlige vinkelhastigheten.
I en jevn rotasjonsbevegelse kalles tiden for en fullstendig revolusjon periode og er betegnet med T.
Videre, når en fullstendig sving er gjort, er den tilbakelagte vinkelen 2π, så i en jevn rotasjon er vinkelhastigheten ω relatert til perioden T, med følgende formel:
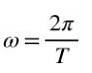
Den definerer Frekvens F med en jevn rotasjon som kvotienten mellom antall svinger og tiden som brukes til å gå gjennom dem, det vil si hvis N svinger blir gjort i tidsperioden Δt, vil frekvensen være:
f = N / At
Siden en sving (N = 1) er reist i tid T (perioden), oppnås følgende forhold:
f = 1 / T
Det vil si at i en jevn rotasjon er vinkelhastigheten relatert til frekvensen gjennom forholdet:
ω = 2π ・ f
Forholdet mellom vinkelhastighet og lineær hastighet
Lineær hastighet v, er kvotienten mellom den tilbakelagte avstanden og tiden det tar å reise den. I figur 2 er den tilbakelagte avstanden buelengden Δs.
Buen Δs er proporsjonal med den vinklede Δϕ og radien r, og følgende forhold oppfylles:
Δs = r ・ Δϕ
Så lenge Δϕ måles i radianer.
Hvis vi deler det forrige uttrykket med tidsforløpet Δt, får vi:
(Δs / Δt) = r ・ (Δϕ / Δt)
Kvotienten til det første elementet er den lineære hastigheten og kvoten for det andre elementet er den gjennomsnittlige vinkelhastigheten:
v = r ・ ω
Løst øvelser
-Øvelse 1
Spissene på bladene til takviften vist i figur 1 beveger seg med en hastighet på 5 m / s, og bladene har en radius på 40 cm.
Beregn med disse dataene: i) hjulets gjennomsnittlige vinkelhastighet, ii) antall omdreininger hjulet gjør på ett sekund, iii) perioden i sekunder.
Løsning
i) Den lineære hastigheten er v = 5 m / s.
Radien er r = 0,40 m.
Fra forholdet mellom lineær hastighet og vinkelhastighet løser vi det siste:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 omdreininger / s
iii) T = 1 / f = 1 / (2 omdreininger / s) = 0,5 s for hver sving.
-Øvelse 2
En leketøybarn beveger seg på et sirkulært spor med en radius på 2m. Ved 0s er vinkelposisjonen 0 rad, men etter tid t er vinkelposisjonen
φ (t) = 2 ・ t .
Med disse dataene
i) Beregn den gjennomsnittlige vinkelhastigheten i de følgende tidsintervallene [0s, 0,5s]; [0,5s, 1,0s]; [1.0s, 1.5s] og til slutt i perioden [0.0s, 1.5s].
ii) Basert på resultatene fra del i) Hva kan sies om bevegelsen?
iii) Bestem den gjennomsnittlige lineære hastigheten i samme tidsperiode fra del i)
iv) Finn vinkelhastighet og lineær hastighet for ethvert øyeblikk.
Løsning
i) Den gjennomsnittlige vinkelhastigheten er gitt av følgende formel:
Vi fortsetter å beregne den tilbakelagte vinkelen og tiden som har gått i hvert intervall.
Intervall 1: Δϕ = ϕ (0.5s) - ϕ (0.0s) = 2 (rad / s) * 0.5s - 2 (rad / s) * 0.0s = 1.0 rad
Δt = 0,5s - 0,0s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Intervall 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad / s) * 1.0s - 2 (rad / s) * 0.5s = 1.0 rad
Δt = 1.0s - 0.5s = 0.5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Intervall 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad / s) * 1.5s - 2 (rad / s) * 1.0s = 1.0 rad
Δt = 1,5s - 1,0s = 0,5s
ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s
Intervall 4: Δϕ = ϕ (1,5s) - ϕ (0,0s) = 2 (rad / s) * 1,5s - 2 (rad / s) * 0,0s = 3,0 rad
Δt = 1,5s - 0,0s = 1,5s
ω = Δϕ / Δt = 3,0rad / 1,5s = 2,0 rad / s
ii) Med tanke på de forrige resultatene, der den gjennomsnittlige vinkelhastigheten ble beregnet i forskjellige tidsintervaller, og alltid oppnådde det samme resultatet, ser det ut til å indikere at det er en ensartet sirkelbevegelse. Disse resultatene er imidlertid ikke avgjørende..
Måten å sikre konklusjonen er å beregne den gjennomsnittlige vinkelhastigheten for et vilkårlig intervall [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
Dette betyr at leketøyvognen har en konstant gjennomsnittlig vinkelhastighet på 2 rad / s i løpet av en hvilken som helst periode. Men du kan gå lenger hvis du beregner øyeblikkelig vinkelhastighet:
Dette tolkes som at lekebilen til enhver tid har konstant vinkelhastighet = 2 rad / s.
Referanser
- Giancoli, D. Fysikk. Prinsipper med applikasjoner. 6. utgave. Prentice Hall. 30-45.
- Kirkpatrick, L. 2007. Fysikk: En titt på verden. 6ta Forkortet utgave. Cengage læring. 117.
- Resnick, R. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 33-52.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Utgave. Mexico. Cengage Learning Editors. 32-55.
- Wikipedia. Vinkelhastighet. Gjenopprettet fra: wikipedia.com



Ingen har kommentert denne artikkelen ennå.