
5 Multiplikative problemer for barn
De mangfoldige problemer De blir undervist til barn i grunnskolen, etter å ha lært fakta om addisjon og subtraksjon, også kalt addisjon og subtraksjon..
Det er viktig å lære barn at multiplikasjon av hele tall egentlig er en sum, men det er viktig å lære å formere seg for å gjøre disse tilleggene raskere og enklere.

Det er viktig å velge de første problemene som skal brukes til å lære barn å formere seg godt, ettersom de må være problemer de kan forstå og kan se nytten av å lære å formere seg..
Det er ikke nok å bare lære dem multiplikasjonstabellene mekanisk, det er mye mer attraktivt å vise dem deres bruk gjennom situasjoner som oppstår i hverdagen, for eksempel når foreldrene deres handler.
Eksempler på multiplikasjonsproblemer
Det er mange problemer som kan brukes til å lære et barn å bruke multiplikasjonstabeller. Nedenfor er noen problemer med løsningene.
1- Hvor mange bøker som er igjen å bestille?
En bibliotekar må sortere bøkene i bibliotekshyllene. På slutten av fredag ettermiddag innser bibliotekaren at han fortsatt trenger å bestille 78 bokser med bøker, som har 5 bøker hver. Hvor mange bøker vil bibliotekaren måtte bestille neste uke?

Løsning: I dette problemet skal det bemerkes at alle bokser har samme antall bøker. Derfor representerer 1 boks 5 bøker, 2 bokser representerer 5 + 5 = 10 bøker, 3 bokser representerer 5 + 5 + 5 = 15 bøker. Men å gjøre alle disse summene er en veldig omfattende prosess.
Å gjennomføre alle ovennevnte summer tilsvarer å multiplisere antall bøker i hver boks med antall rester som er igjen å bestille. Nemlig, 5 × 78, derfor trenger bibliotekaren å bestille 390 bøker.
2- Hvor mange bokser trenger bonden?
En bonde må pakke kaffen som ble oppnådd i sin siste høst, i esker. Den totale innhøstingen er 20 000 kilo, og boksene du skal pakke dem har en maksimal kapasitet på 100 kilo. Hvor mange bokser trenger bonden for å pakke hele høsten?
Løsning: Det første du må merke er at alle boksene har samme kapasitet (100 kilo). Så hvis bonden bruker 2 bokser, kan han bare pakke 100 + 100 = 200 kilo. Hvis du bruker 4 bokser, vil du pakke 200 + 200 = 400 kilo.
Som før er det en veldig lang prosess å gjøre alt dette tilskuddet. Nøkkelen er å finne et tall som når multiplisert med 100 er resultatet 20 000.
Ved å undersøke i detalj kan det sees at dette tallet er 200, siden 200 × 100 = 20.000.
Derfor trenger bonden 200 bokser for å pakke hele innhøstingen..
3- Hvor mange vinduer er det?
Maria flyttet nettopp inn i en bygning og vil gjerne vite hvor mange vinduer bygningen har foran. Bygningen har 13 etasjer og i hver etasje er det 3 vinduer.
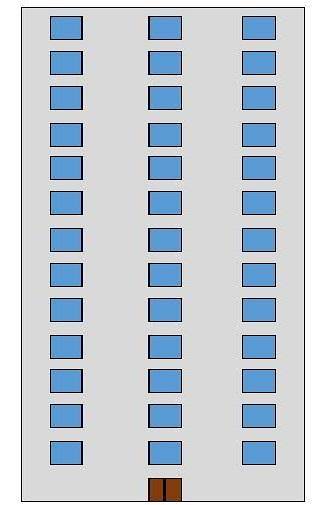
Løsning: i dette problemet kan du telle antall vinduer gulv for gulv og legge dem til for å få svaret.
Men siden hver etasje har samme antall vinduer, er det mye raskere å multiplisere antall etasjer med antall vinduer i hver etasje. Det vil si 13 × 3, derfor har bygningen 39 vinduer.
4- Hvor mange fliser trenger du?
Javier er en murer som bygger et badegulv. Så langt har Javier plassert 9 fliser (firkanter) på badegulvet som vist i figuren nedenfor. Hvor mange fliser skal til for å dekke hele baderomsgulvet?
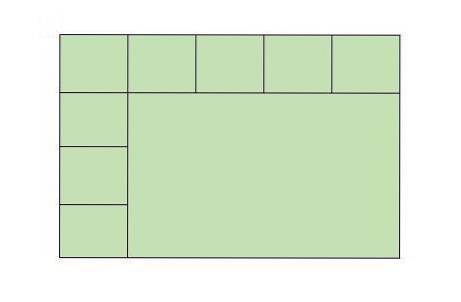
Løsning- En måte å løse dette problemet er å fylle ut figuren ved å tegne de manglende flisene og deretter telle dem.
Men i følge bildet kan badegulvet passe 5 fliser horisontalt og 4 vertikalt. Derfor vil hele baderomsgulvet ha totalt 5 × 4 = 20 fliser.
5- Hva er totalt antall dager?
Månedene januar, mars, mai, juli, august, oktober og desember har 31 dager hver. Hva er det totale antallet dager som alle disse månedene legger opp til??

Løsning: i denne øvelsen er data eksplisitt gitt som er antall dager (31). De andre dataene er gitt implisitt i måneder (7). Derfor er de totale dagene mellom alle disse månedene 7 × 31 = 217.
Referanser
- Aristoteles, P. (2014). 150 matematiske problemer for primærrommet (bind 1). Aristoteles-prosjektet.
- Aristoteles, P. (2014). 150 matematikkproblemer for femte klasse primær (bind 1). Aristoteles-prosjektet.
- Broitman, C. (1999). Operasjoner i første syklus: bidrag til arbeid i klasserommet (omtrykk red.). Noveduc Books.
- Coffland, J., og Cuevas, G. (1992). Primær problemløsning i matematikk: 101 aktiviteter. Gode årsbøker.
- Nunes, T., og Bryant, P. (2003). Matematikk og dens anvendelse: Barnets perspektiv. XXI århundre.
- Riley, J., Eberts, M., & Gisler, P. (2005). Matematisk utfordring: morsomme og kreative problemer for barn, nivå 2. Gode årsbøker.
- Rodríguez, J. M. (2003). Læring og lek: utdanningsaktiviteter ved bruk av Prismaker System leken-didaktisk materiale (illustrert utg.). (U. d.-L. Mancha, red.) Univ de Castilla La Mancha.
- Souviney, R. J. (2005). Løse matematiske problemer Barn bryr seg om. Gode årsbøker.



Ingen har kommentert denne artikkelen ennå.