Definisjon av sentripetal akselerasjon, formler, beregning, øvelser

De sentripetal akselerasjon til_c, Også kalt radial eller normal, det er akselerasjonen som en bevegelig gjenstand bærer når den beskriver en sirkulær bane. Størrelsen er v^to/ r, hvor r er sirkelens radius, den er rettet mot sentrum av den og er ansvarlig for å holde mobilen på vei.

Dimensjonene til sentripetal akselerasjon er lengde per tidsenhet i kvadrat. I det internasjonale systemet er de m / s^to. Hvis sentripetal akselerasjon av en eller annen grunn forsvinner, gjør også kraften som tvinger mobilen til å opprettholde den sirkulære banen.

Dette er hva som skjer med en bil som prøver å svinge på et flatt, isete spor, der friksjonen mellom bakken og hjulene er utilstrekkelig for at bilen skal svinge. Derfor er den eneste muligheten som gjenstår å bevege seg i en rett linje, og det er derfor den forlater kurven.

Artikkelindeks

• 1 Sirkulære bevegelser
• 2 Sentripetalkraften
• 3 Formler for sentripetal akselerasjon
• 4 Øvelse løst
  • 4.1 Svar
• 5 Referanser

Sirkulære bevegelser

Når et objekt beveger seg i en sirkel, er sentripetal akselerasjon til enhver tid rettet radialt mot sentrum av omkretsen, en retning som er vinkelrett på banen som følges.

Siden hastighet alltid er tangent til banen, viser hastighet og sentripetal akselerasjon å være vinkelrett. Derfor har ikke hastighet og akselerasjon alltid samme retning.

Under disse omstendighetene har mobilen muligheten til å beskrive omkretsen med konstant eller variabel hastighet. Det første tilfellet er kjent som Uniform Circular Movement eller MCU for dets forkortelse, det andre tilfellet vil være en Variable Circular Movement.

I begge tilfeller er sentripetal akselerasjon ansvarlig for å holde mobilen spinnende, og sørger for at hastigheten bare varierer i retning og i retning.

For å ha en variabel sirkulær bevegelse, vil det imidlertid være nødvendig med en annen komponent av akselerasjonen i samme retning av hastigheten, som har ansvaret for å øke eller redusere hastigheten. Denne komponenten av akselerasjon er kjent som tangentiell akselerasjon.

Variabel sirkelbevegelse og kurvlinjær bevegelse generelt har begge akselerasjonskomponenter, fordi kurvlinjær bevegelse kan forestilles som banen gjennom utallige omkretsbuer som utgjør den buede banen..

Den sentripetale kraften

Nå er en styrke ansvarlig for å gi akselerasjonen. For en satellitt som kretser rundt jorden er det tyngdekraften. Og siden tyngdekraften alltid virker vinkelrett på banen, endrer den ikke satellittens hastighet..

I et slikt tilfelle fungerer tyngdekraften som en sentripetal kraft, som ikke er en spesiell eller separat kraftklasse, men en som i tilfelle satellitten er rettet radielt mot sentrum av jorden.

I andre typer sirkulær bevegelse, for eksempel en bil som dreier en kurve, blir sentripetalkraftens rolle spilt av statisk friksjon, og for en stein bundet til et tau som roteres i sirkler, er spenningen i tauet kraften som tvinger mobil for å spinne.

Formler for sentripetal akselerasjon

Den sentripetale akselerasjonen beregnes av uttrykket:

ac = v^to/ r

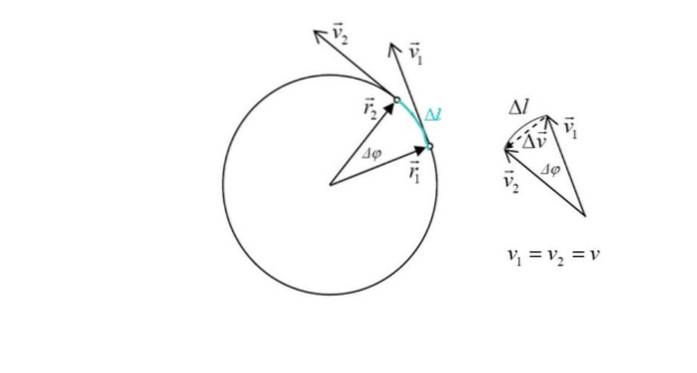
Dette uttrykket vil bli avledet nedenfor. Per definisjon er akselerasjon endringen i hastighet over tid:

Mobilen tar tid Δt i ruten, som er liten, siden punktene er veldig nærme.

Figuren viser også to posisjonsvektorer r₁ Y r_to, hvis modul er den samme: radiusen r av omkretsen. Vinkelen mellom de to punktene er Δφ. I grønt fremhever Bue krysset av mobilen, betegnet som Δl.

På figuren til høyre ser man at størrelsen på Δv, endringen i hastighet er omtrent proporsjonal med Δl, siden vinkelen Δφ er liten. Men hastighetsendringen er nettopp relatert til akselerasjon. Fra trekanten kan det sees ved å legge til vektorene som:

v₁ + Δv = v_to → Δv = v_to - v₁

Δv det er interessant, siden det er proporsjonalt med sentripetal akselerasjon. Fra figuren kan det sees at siden vinkelen Δφ er liten, er vektoren Δv er i det vesentlige vinkelrett på begge deler v₁ som v_to og peker på midten av omkretsen.

Selv om vektorene frem til nå er fremhevet med fet skrift, arbeider vi med modulene eller størrelsen på disse vektorene for å få effekten av geometrisk natur som følger, og dispensere med vektornotasjonen.

Noe annet: du må bruke definisjonen av sentral vinkel, som er:

Δφ= Δl / r

Nå sammenlignes begge figurene, som er proporsjonale siden vinkelen Δφ det er vanlig:

Deling av Δt:

til_c= v^to/ r

Treningen løst

En partikkel beveger seg i en sirkel med en radius på 2,70 m. I et gitt øyeblikk er akselerasjonen 1,05 m / s^to i en retning som gir en vinkel på 32,0º med bevegelsesretningen. Beregn hastigheten din:

a) På den tiden

b) 2,00 sekunder senere, forutsatt konstant tangentiell akselerasjon.

Svar

Det er en variert sirkulær bevegelse, siden uttalelsen indikerer at akselerasjonen har en gitt vinkel med bevegelsesretningen som verken er 0 ° (det kan ikke være en sirkelbevegelse) eller 90 ° (det vil være en ensartet sirkulær bevegelse).

Derfor eksisterer de to komponentene - radial og tangensiell - sammen. De vil bli betegnet som en_c allerede_t og er tegnet i følgende figur. Vektoren i grønt er netto akselerasjonsvektor eller bare akselerasjon til.

a) Beregning av akselerasjonskomponentene

til_c = a.cos θ = 1,05 m / s^to . cos 32,0º = 0,89 m / s^to (i rødt)

til_t = a.sen θ = 1,05 m / s^to . sin 32,0º = 0,57 m / s^to (i oransje)

Beregning av hastigheten på mobilen

Siden en_c = v^to/ r, deretter:

v = v_eller +til_t. t = 1,6 m / s + (0,57 x 2) m / s = 2,74 m / s

Referanser

1. Giancoli, D. Fysikk. 2006. Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Konseptuell fysikk. Femte utgave.Pearson.106-108.