Radiell belastning hvordan man beregner det, løste øvelser

De radiell belastning Det er kraften som utøves vinkelrett på et objekts symmetriakse og hvis handlingslinje går gjennom denne aksen. For eksempel påfører et belte på en remskive en radiell belastning på lageret eller lageret på remskiveakselen..

I figur 1 representerer de gule pilene radiale krefter eller belastninger på akslene på grunn av spenningen til beltet som passerer gjennom remskivene..

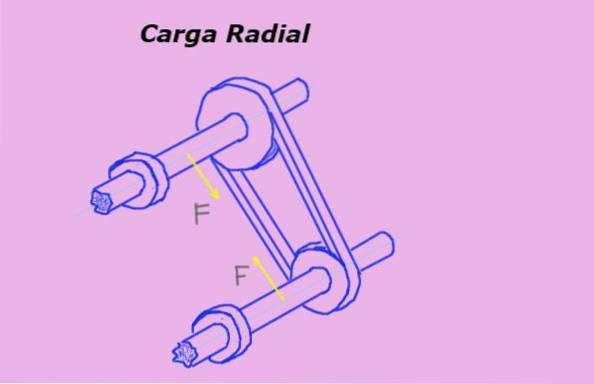
Måleenheten for radiell belastning i det internasjonale systemet eller SI-systemet er Newton (N). Men andre kraftenheter brukes også ofte til å måle den, for eksempel kilokraften (Kg-f) og pundkraften (lb-f).

Artikkelindeks

• 1 Hvordan beregnes det? 
• 2 Løst øvelser
  • 2.1-Øvelse 1
  • 2.2 Øvelse 2
• 3 Referanser

Hvordan beregnes det? 

For å beregne verdien av den radiale belastningen på elementene i en struktur, må følgende trinn følges:

- Lag diagrammet over krefter på hvert element.

- Bruk ligningene som garanterer translasjonell likevekt; det vil si at summen av alle kreftene er null.

- Tenk på ligningen av dreiemomenter eller momenter slik at rotasjonsvekt er oppfylt. I dette tilfellet må summen av alle momentene være null.

- Beregn kreftene for å kunne identifisere de radiale belastningene som virker på hvert av elementene.

Løst øvelser

-Øvelse 1

Følgende figur viser en remskive gjennom hvilken en strammet remskive går med spenning T. Remskiven er montert på en aksel støttet av to lagre. Sentrum av en av dem er på avstand L.₁ fra midten av remskiven. I den andre enden er det andre lageret, på avstand L_to.

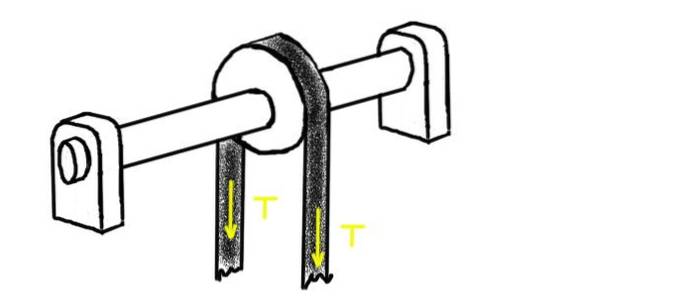
Bestem den radiale belastningen på hvert av lagrene, forutsatt at vekten på akselen og remskiven er betydelig mindre enn påført spenning.

Ta som verdi for beltespenningen 100 kg-f og for avstandene L₁= 1 m og L._to= 2 m.

Løsning

Først lages et diagram over kreftene som virker på aksen.

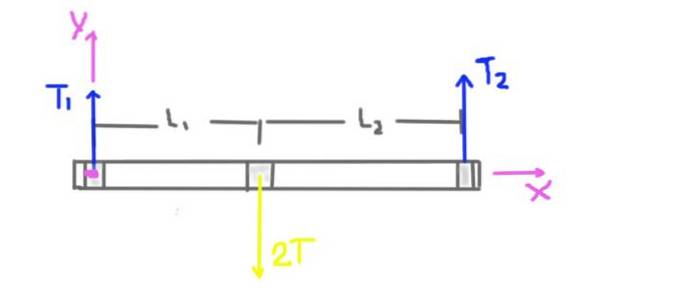
Remskivespenningen er T, men den radiale belastningen på akselen ved remskiven er 2T. Vekten på akselen og remskiven tas ikke i betraktning fordi uttalelsen om problemet forteller oss at den er betydelig mindre enn spenningen som påføres beltet.

Den radiale reaksjonen av støttene på akselen er forårsaket av de radiale kreftene eller belastningene T1 og T2. Avstandene L1 og L2 fra støttene til midten av remskiven er også angitt i diagrammet..

Koordinatsystemet vises også. Dreiemomentet eller totalmomentet på aksen vil bli beregnet ved å ta sentrum som koordinatsystemets opprinnelse og være positivt i Z-retning.

Likevektsforhold

Nå er likevektsbetingelsene etablert: summen av krefter er lik null og summen av dreiemoment er lik null.

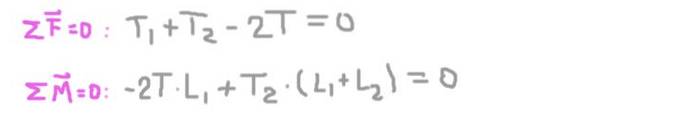
Fra den andre ligningen får vi den radiale reaksjonen på aksen i bæreren 2 (T_to), erstatter i den første og løser den radiale reaksjonen på aksen ved støtte 1 (T₁).

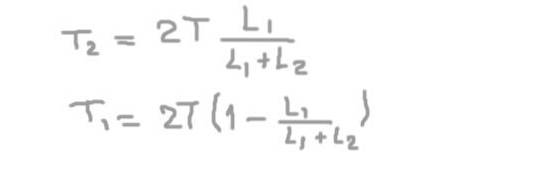
T₁= (2/3) T = 66,6 kg-f

Og den radiale belastningen på akselen i posisjonen til støtten 2 er:

T_to= (4/3) T = 133,3 kg-f.

Øvelse 2

Følgende figur viser et system som består av tre remskiver A, B, C alle med samme radius R. Remskivene er forbundet med et belte som har en spenning T.

Aksler A, B, C går gjennom smurte lagre. Skillet mellom sentrum av aksene A og B er 4 ganger radien R. Tilsvarende er skillet mellom aksene B og C også 4R.

Bestem den radiale belastningen på aksene til remskivene A og B, forutsatt at beltestrammingen er 600N.

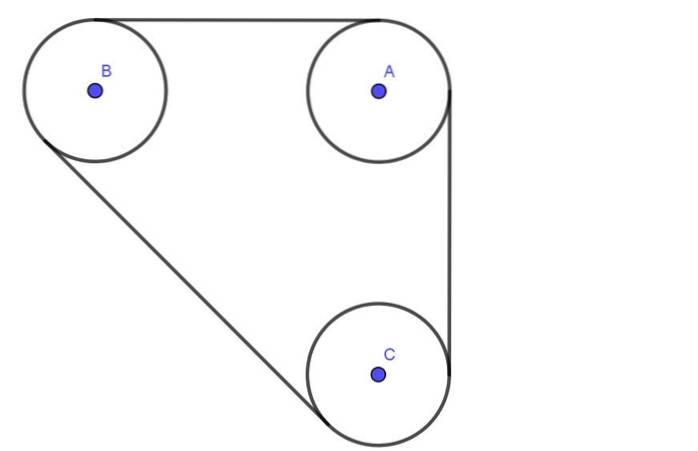
Løsning

Vi begynner med å tegne et diagram over kreftene som virker på remskive A og B. På den første har vi de to spenningene T₁ og T_to, så vel som kraften F_TIL at lageret utøver på remskivens akse A.

På samme måte har vi på remskive B spenningene T₃ , T₄ og styrken F_B at lageret utøver på aksen til det samme. Den radiale belastningen på remskiven A er kraften F_TIL og den radiale belastningen på B er kraften F_B.

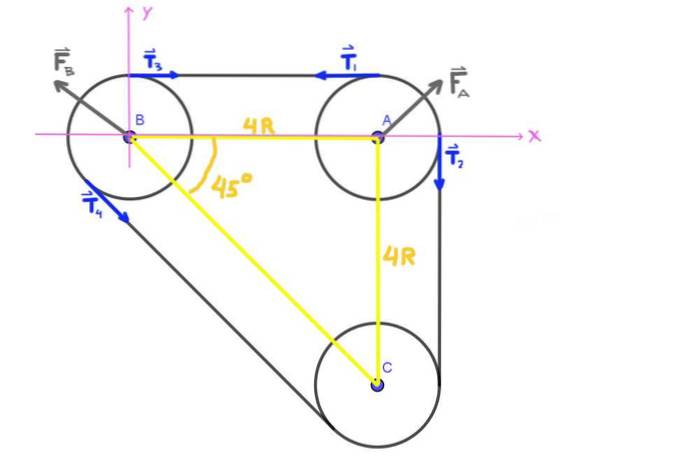
Siden aksene A, B, C danner en isorektangel-trekant, er vinkelen ABC 45 °.

Alle spenninger T₁ , T_to , T₃ , T₄ vist i figuren har samme modul T, som er beltestrammingen.

Balanseforhold for remskive A

Nå skriver vi likevektstilstanden for remskive A, som ikke er noe annet enn summen av alle kreftene som virker på remskive A, må være null.

Å skille X- og Y-komponentene i kreftene og legge til (vektorielt) følgende par skalære ligninger oppnås:

F_TILX - T = 0; F_TILY - T = 0

Disse ligningene fører til følgende likhet: F_ØKS = F_ÅH = T.

Derfor har den radiale belastningen størrelsen gitt av:

F_TIL = (T² + T²)^1/2 = 2^1/2∙ T = 1,41 ∙ T = 848,5 N. med 45 ° retning. 

Balanseforhold for remskive B

På samme måte skriver vi likevektstilstanden for remskive B. For komponent X har vi: F_BX + T + T ∙ Cos45 ° = 0

Y for komponent Y: F_BY + T ∙ Sen45 ° = 0

Og dermed:

F_BX = - T (1 + 2^-1/2) og F_AV = -T ∙ 2^-1/2

Det vil si at størrelsen på den radiale belastningen på remskiven B er:

F_B = ((1 + 2^-1/2) ² + 2^-1)^1/2∙ T = 1,85 ∙ T = 1108,66 N og dens retning er 135 °.

Referanser

1. Beer F, Johnston E, DeWolf J, Mazurek, D. Materialmekanikk. Femte utgave. 2010. Mc Graw Hill. 1-130.
2. Gere J, Goodno, B. Materialmekanikk. Åttende utgave. Cengage læring. 4-220.
3. Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. 6^tth Ed. Prentice Hall. 238-242.
4. Hibbeler R. Materialmekanikk. Åttende utgave. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Notater om generell fysikk. UNAM. 87-98.